- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
1.4. Задача про мінімізацію відходів
Модель задачі про раціональний розкрій матеріалів має важливе значення для економії матеріалів і сировини. Розглянемо постановку задачі.
На
розкрій надходить матеріал у вигляді
певних одиниць стандартних розмірів.
Потрібно з нього виготовити
![]() різних виробів. Задано асортимент цих
виробів, тобто
різних виробів. Задано асортимент цих
виробів, тобто![]() – відповідно нижня і верхня границі
кількості виробівi-го
виду. Кожна одиниця вихідного матеріалу
може бути розкроєна
– відповідно нижня і верхня границі
кількості виробівi-го
виду. Кожна одиниця вихідного матеріалу
може бути розкроєна
![]() різними способами, причому використанняj-го
способу дає
різними способами, причому використанняj-го
способу дає
![]() одиницьi-го
виробу
одиницьi-го
виробу
![]() .
Відома величина відходів
.
Відома величина відходів![]() з одиниці стандартного матеріалу приj-му
способі розкрою.
з одиниці стандартного матеріалу приj-му
способі розкрою.
Необхідно знайти план розкрою, що забезпечує заданий асортимент виробів при мінімальних сумарних відходах матеріалів.
За
невідому
![]() беремочисло
одиниць вихідного
матеріалу, що потрібно розкроїти j-v
способом, тоді
беремочисло
одиниць вихідного
матеріалу, що потрібно розкроїти j-v
способом, тоді
![]() – план розкрою.Через
– план розкрою.Через
![]() позначимо загальну кількість відходів.
Кількість заготовокi-го
виду запишемо у вигляді
позначимо загальну кількість відходів.
Кількість заготовокi-го
виду запишемо у вигляді
![]() .
.
Тоді математична модель задачі має вигляд:

![]() .
.
Характер моделі може змінитися, якщо в умові задати іншу мету. Наприклад, якщо ставиться задача про одержання заданої кількості виробів з найменшою кількістю вихідного матеріалу, то функція мети має вигляд:
![]()
Побудувати математичну модель задачі.
Задача 1.4. Рулони лінолеуму довжиною 30 м треба розрізати на шматки довжиною 15, 10 та 6 м. Причому шматків по 15 м необхідно не більш 20, шматків по 10 м – не менш 16, а шматків по 6 м – не менше 12 та не більше 22. Визначити оптимальний план розкрою лінолеуму з точки зору мінімізації відходів.
Рішення
Позначимо
через a1,
a2
та a3
кількість шматків довжиною відповідно
15, 10 та 6 м, що можуть бути одержані з
одного рулону лінолеуму. Відповідно до
умови задачі, вектор
![]() визначає спосіб розкрою рулону лінолеуму
тоді і тільки тоді, коли виконана умова
0 ≤ 30 – (15а1
+ 10а2
+ 6а3)
< min{15; 10; 6} = 6.
визначає спосіб розкрою рулону лінолеуму
тоді і тільки тоді, коли виконана умова
0 ≤ 30 – (15а1
+ 10а2
+ 6а3)
< min{15; 10; 6} = 6.
Для визначення усіх можливих способів розкрою побудуємо відповідне дерево пошуку.
0
30303000
30
20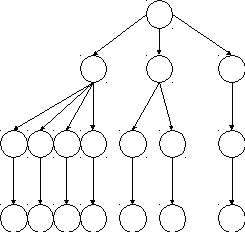
К 2ількість шматків
д
1
0
30
0
3
0
1
15
0
15
2
1
0
2
Кількість
шматків
0
0
0
довжиною
10 м
10
5
Кількість
шматків
0
2
1
довжиною
6 м
0
0
5
3
0
3
5
Величина
відходів
4
Рис. 1.1
Вершини, що є кінцями шляхів, визначають величину відходів, отриманих після розкрою матеріалу. З рисунка видно, що усього існує 7 допустимих способів розкрою рулону лінолеуму. Запишемо ці способи розкрою у табл. 1.7.
Таблиця 1.7
|
Кількість шматків довжиною, м |
Способи розкрою рулону лінолеуму | ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
15 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
|
10 |
0 |
1 |
2 |
3 |
0 |
1 |
0 |
|
6 |
5 |
3 |
1 |
0 |
2 |
0 |
0 |
|
Величина відходів |
0 |
2 |
4 |
0 |
3 |
5 |
0 |
Позначимо через xj кількість рулонів лінолеуму, що розкроюються j-м способом ( j = 1, 2, …, 7).
План
розкрою визначається вектором
![]() .
.
Умови забезпечення необхідного асортименту задаються нерівностями:
![]() .
.
При
реалізації плану
![]() сумарна величина відходів є значенням
функції
сумарна величина відходів є значенням
функції
![]() .
.
Таким чином, ми отримали наступну математичну модель: