
- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
1.2. Задача складання раціону (задача про дієту, задача про суміші)
Ще один клас моделей виникає з економічних проблем, пов’язаних з виготовленням різних сумішей:
у сільськогосподарському виробництві при визначенні складу добрив;
при використанні різних видів пального для отримання пального іншої марки;
в металургії при виготовленні сталі з кількох марок сталі;
при складанні раціону харчування сім’ї, спортсменів, худоби.
Початкові дані наведені в табл. 1.3.
Таблиця 1.3
|
Вид компонента |
Вага
i-го
компонента (кг)
в одному кг j-го
матеріалу
|
Потрібна вага компонента в суміші, кг | |||||
|
1 |
2 |
... |
|
... |
| ||
|
1 |
|
|
... |
|
... |
|
|
|
2 |
|
|
... |
|
... |
|
|
|
... |
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
... |
|
|
|
... |
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
... |
|
|
|
Ціна 1 кг матеріалу, грн/кг |
|
|
... |
|
... |
|
|
|
Загальна вага матеріалу в суміші, кг |
|
|
... |
|
... |
|
|
У таблиці позначено:
![]() –вага
i-го
компонента (кг) в одному кг j-го
матеріалу;
–вага
i-го
компонента (кг) в одному кг j-го
матеріалу;
![]() – потрібна вагаi-го
компонента у вихідній суміші;
– потрібна вагаi-го
компонента у вихідній суміші;
![]() – ціна одного кг
j-го
матеріалу. Ці показники вважаються
постійними, тобто
– ціна одного кг
j-го
матеріалу. Ці показники вважаються
постійними, тобто
![]()
![]() .
.
![]() –загальна
вага j-го
матеріалу в суміші
–загальна
вага j-го
матеріалу в суміші
![]() .
.
Завдання:
отримати
суміш
![]() мінімальної вартості
мінімальної вартості![]() .
.
Математичний
опис задачі складається з функції мети
![]()
та
обмежень:
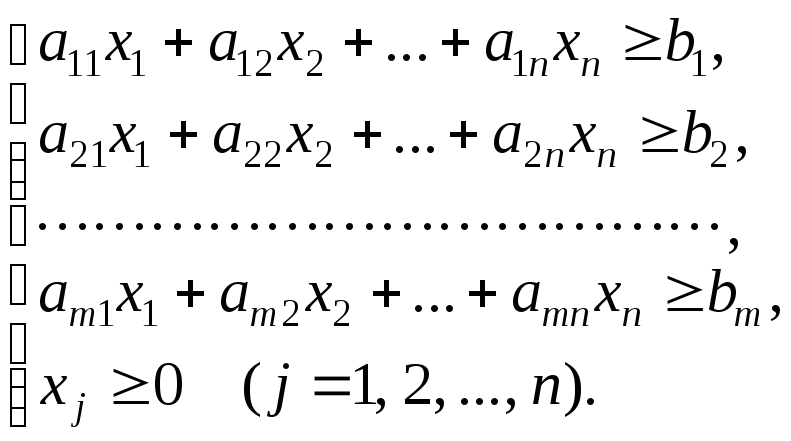
Побудувати математичну модель задачі.
Задача 1.2. До добового раціону сім’ї входять два продукти: м’ясо і фрукти. Щодо кожного з продуктів відомо: скільки в одному кілограмі міститься білка, вітаміну А, вітаміну В, вітаміну С та вартість одного кілограму м’яса та фруктів. Обчислити загальну вагу продуктів у раціоні мінімальної вартості, при умові, що у сукупності всі продукти повинні містити не менше заданої кількості компонентів (білка, вітаміну А, вітаміну В, вітаміну С).
Таблиця 1.4
|
Вид компонента |
Вага компонента (у. о.) в одному кг продукту |
Потрібна вага компонента в раціоні, у. о. | |
|
Продукт №1 |
Продукт №2 | ||
|
Білок |
17 |
0,9 |
10 |
|
Вітамін А |
0,09 |
12 |
4 |
|
Вітамін В |
4,1 |
- |
1 |
|
Вітамін С |
- |
7,1 |
1 |
|
Ціна 1 кг продукту, грн/кг |
45 |
19 |
|
Рішення
Побудуємо математичну модель задачі.
Позначимо
через хj
–
загальну
вагу продукту
j-го
виду (j=1,
2) в раціоні. Тоді цей раціон буде містити
![]() одиниць білка,
одиниць білка,![]() одиниць вітамінуА,
одиниць вітамінуА,
![]() одиниць вітамінуВ
і
одиниць вітамінуВ
і
![]() одиниць вітамінуС.
Оскільки ці кількості поживних речовин
в раціоні не можуть бути менше заданих
границь, відповідно 10, 4, 1 і 1, то маємо
систему нерівностей:
одиниць вітамінуС.
Оскільки ці кількості поживних речовин
в раціоні не можуть бути менше заданих
границь, відповідно 10, 4, 1 і 1, то маємо
систему нерівностей:
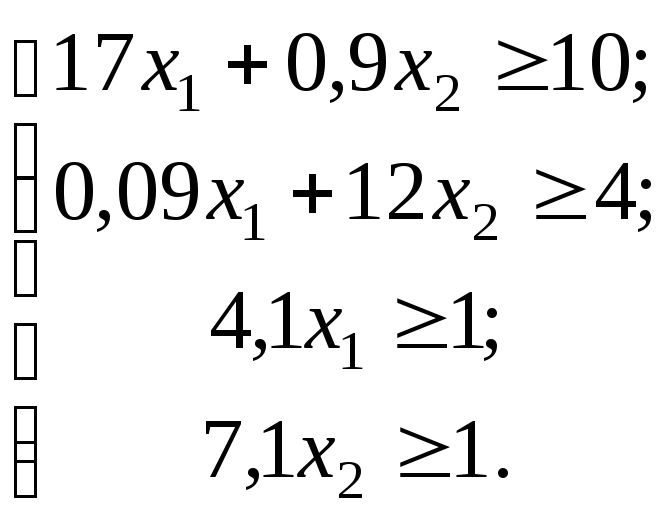 (1.4)
(1.4)
Загальна вартість раціону
![]() (1.5)
(1.5)
Таким
чином, математична модель задачі
складання раціону така: скласти
добовий раціон
![]() ,
що задовольнить системі (1.4),
при якому функція (1.5)
набуде мінімального значення.
,
що задовольнить системі (1.4),
при якому функція (1.5)
набуде мінімального значення.
