9.2. Задача про заміну обладнання

Задача 9.2. Обладнання експлуатується протягом 5 років, після цього продається. На початку кожного року можна прийняти рішення зберегти облад-нання або замінити його новим. Вартість нового обладнання грн. Післяt років експлуатації () обладнання можна продати загрн (ліквідна вартість). Витрати на експлуатацію протягом року залежать від вікуt обладнання і дорівнюють . Визначити оптимальну стратегію експлуатації обладнання, щоб сумарні витрати з урахуванням початкової покупки і заключного продажу були мінімальні.

Рішення

Спосіб розподілу процесу управління на кроки: номер кроку – номер року, n=5. Параметр стану – вікtобладнання,,– на початку першого року експлуатації обладнання нове. Управління на кожному кроці залежить від двох змінних(не замінити) і(замінити обладнання).

Рівняння станів мають вид:

k=1, 2, 3, 4. (9.8)

Дійсно, якщо до k-го кроку (до початку k-го року) , то при збереженні обладнання () через рік його вік збільшиться на 1, тобто . Якщо обладнання замінюється новим (), то це означає, що до початку k-го кроку його вік t=0, а після року експлуатації t=1, тобто .

Показник ефективності k-го кроку – витрати на експлуатацію обладнання наприкінці k-го року:

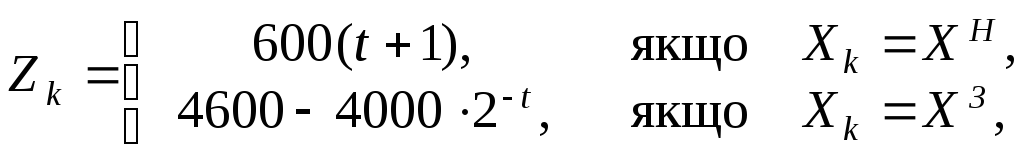k=1, 2, 3, 4. (9.9)

Дійсно, при збереженні обладнання () витрати пов’язані тільки з експлуатацією обладнання віку t; при заміні () обладнання продається (), купується нове (4000) і експлуатується протягом першого року (600). При цьому загальні витрати дорівнюють ().

Нехай – умовні оптимальні витрати на експлуатацію обладнання за6–k років, починаючи з k-го до 5-го року включно, за умови, що до початку k-го року обладнання має вік t років. Тоді оптимальні витрати за 5 років дорівнюють .

Запишемо рівняння Беллмана (9.3), замінивши задачу максимізації на задачу мінімізації:

Величина є вартістю обладнання вікуtроків (за умов, що облад-нання після 5 років експлуатації продається).

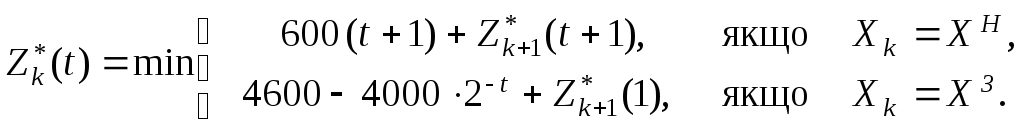
k=4, 3, 2, 1.

Наведемо геометричне рішення цієї задачі. На осі абсцис будемо відкладати номер кроку k, на осі ординат – вік t обладнання. Точка на площині відповідає початкуk-го року експлуатації обладнання віку t років. Переміщення на графіку залежно від обраного управління (зберегти або замінити обладнання) на k-му кроці показані на рис. 9.3 (див. рівняння станів (9.8)).

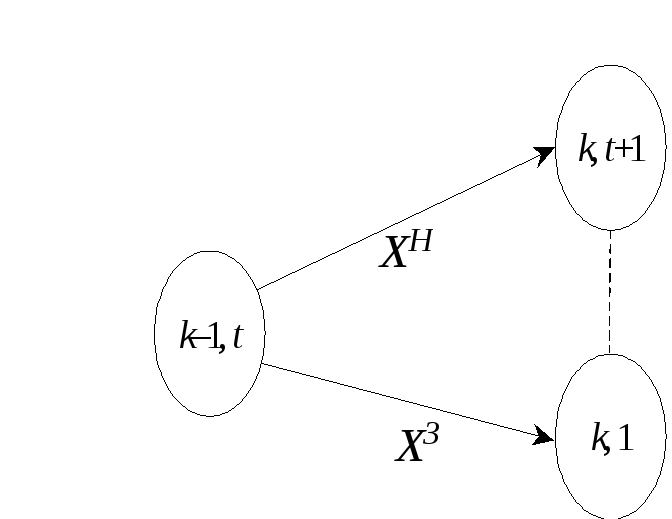
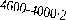
Рис. 9.3

Над кожним відрізком, що з’єднує точки і, запишемо відповідні управліннювитрати, знайдені з (9.9):, а над відрізком, що з’єднує точкиі, запишемо витрати, що відповідають управлінню, тобто. Таким чином ми розмітимо усі відрізки, що з’єднують точки на графіку, і отримаємо рис. 9.6. Наприклад, над відрізком, що з’єднує точкиі, стоїть число 4600, що відповідає витратам на експлуатацію обладнання протягом першого року (купується нове обладнання (4000) і експлуатується протягом року (600)). Над відрізком, що з’єднує точкиі, стоїть число 1200, що відповідає витратам на експлуатацію протягом року обладнання вікуt=1 років (), а над відрізком, що з’єднує точкиі, стоїть число 2600 – це сума витрат на покупку нового обладнання і його експлуатацію протягом року без виторгу за продане обладнання вікуt=1 років ().

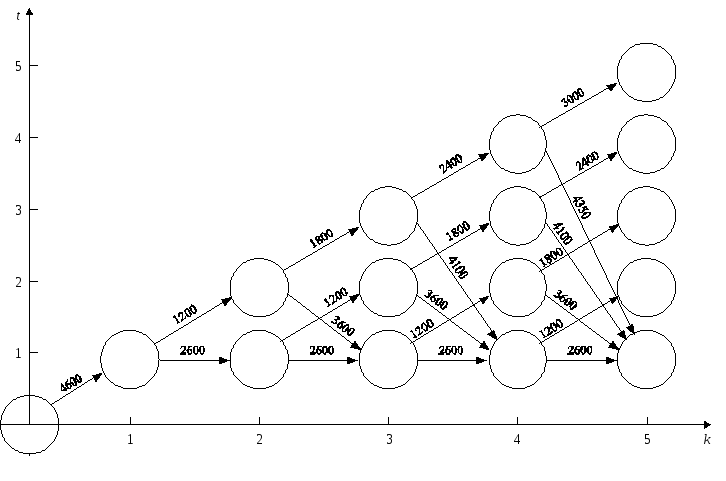
Рис. 9.4

Стан початку експлуатації обладнання відповідає точці , кінець – точкам. Будь-яка траєкторія, що переводить точкузу, складається з відрізків–кроків, кожний з яких відповідає року експлуатації. Треба вибрати таку траєкторію, при якій витрати на експлуатацію обладнання виявляться мінімальними.

Проведемо на розміченому графі станів (рис. 9.4) умовну оптимізацію.

V крок. Початкові стани – точки (4;t), кінцеві (5;t). У станах (5;t) облад-нання продається, умовний оптимальний прибуток від продажу дорівнює , але оскільки цільова функція пов’язана з витратами, то у кружках точок (5;t) поставимо величину доходу зі знаком мінус.

Аналізуємо, як можна потрапити з кожного початкового стану в кінцеве на V кроці.

Стан (4;1). З нього можна потрапити в стан (5;2), витративши на експлуатацію обладнання 1200 і виручивши потім від продажу 1000, тобто сумарні витрати дорівнюють 200, і в стан (5;1) з витратами 2600–2000=600. Виходить, що коли до останнього кроку система перебувала в точці (4;1), то варто йти в точку (5;2) (позначимо цей напрямок подвійною стрілкою), а неминучі мінімальні витрати, що відповідають цьому переходу, дорівнюють 200 (помістимо цю величину у кружок точки (4;1).

Стан (4;2). З нього можна потрапити в стан (5;3) з витратами 1800–500=1300, і в стан (5;1) з витратами 3600–2000=1600. Обираємо перше управління, позначаємо його подвійною стрілкою, а проставляємо у кружок точки (4;2).

Міркуючи в такий спосіб відносно кожної точки передостаннього кроку, знайдемо

,

,

а також відповідні оптимальні управління та позначимо їх на рис. 9.1 подвійною стрілкою.

IV крок. Аналізуємо кожен стан, у якому може бути система наприкінці III кроку з урахуванням оптимального продовження до кінця процесу, тобто вирішуємо для усіх приk=4 рівняння (9.12).

Стан (3;1). З нього можна потрапити в стан (4;2) з витратами 1200+1300=2500 і в стан (4;1) з витратами 2600+200=2800. Вибираємо перше управління, позначаємо його подвійною стрілкою, а значення

проставляємо у кружок точки (3;1). Таким чином підходимо до кожного стану (3;t).

,

.

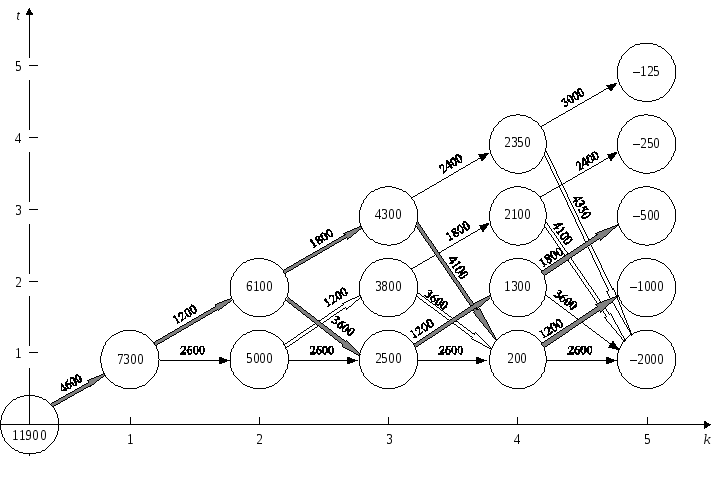
Рис. 9.5

III крок. Знаходимо умовні оптимальні витрати для кожного стану (2;t).

,

.

II крок. .

I крок. .

Далі будуємо оптимальні траєкторії, переміщуючись з точки за подвійними стрілками в. Одержуємо два набори точок:

{(0; 0), (1; 1), (2; 2), (3; 1), (4; 2), (5; 3)},

{(0; 0), (1; 1), (2; 2), (3; 3), (4; 1), (5; 2)}.

Перший набір відповідає оптимальному управлінню , другий –.

Висновок: оптимальний режим експлуатації полягає в тому, щоб замінити обладнання новим на початку 3-го або 4-го року.