
- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
7.1. Графічний метод
Нехай
гра 22
задана
платіжною матрицею
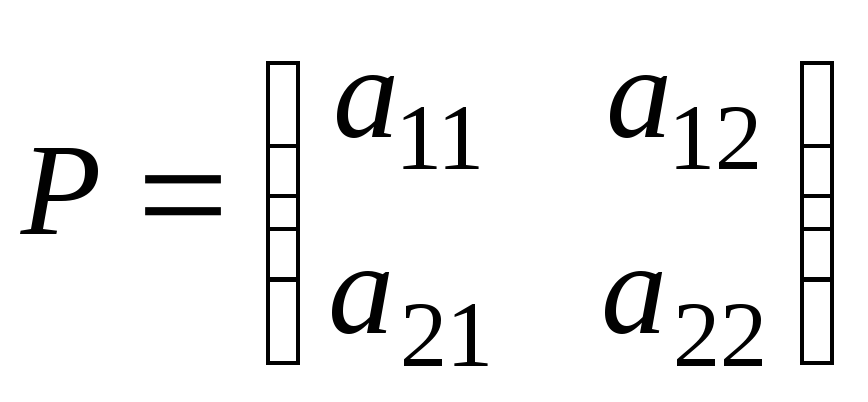 .
Гравець A
має стратегії A1,
A2,
гравець B
– стратегії B1,
B2.
Необхідно визначити оптимальну стратегію
для гравця A,
тобто змішану стратегію
.
Гравець A
має стратегії A1,
A2,
гравець B
– стратегії B1,
B2.
Необхідно визначити оптимальну стратегію
для гравця A,
тобто змішану стратегію
![]() ,
при
застосуванні якої гравець A
отримає максимальний гарантований
середній виграш.
,
при
застосуванні якої гравець A
отримає максимальний гарантований
середній виграш.
Середній виграш (або математичне очікування виграшу) гравця A при застосуванні гравцем B стратегії Bj становить
![]() ,
j=1,
2.
,
j=1,
2.
Гарантований середній виграш гравця A:
![]() .
.
Оскільки
![]() ,
то гарантований виграш гравця A:
,
то гарантований виграш гравця A:
![]() .
.
|
|
Таким
чином,
|
Оптимальну стратегію визначає точка N, у якій гарантований виграш досягає максимуму; її ордината дорівнює ціні гри v.
Геометрично можна також визначити оптимальну стратегію гравця B, якщо поміняти місцями гравців A і B і замість нижньої границі виграшу розглянути верхню границю програшу.
Аналогічний аналіз може бути проведений для ігор 2n, n2.
Задача 7.2. Швейне підприємство, що випускає дитячі сукні й костюми, реалізує свою продукцію через фірмовий магазин. Збут продукції залежить від стану погоди. За даними минулих спостережень підприємство протягом квітня- травня в умовах теплої погоди може реалізувати 600 костюмів і 1975 суконь, а при прохолодній погоді – 1000 костюмів і 625 суконь. Відомо, що витрати на одиницю продукції протягом вказаних місяців склали для костюмів 27 грн, для суконь 8 грн, а ціна реалізації – відповідно 48 і 16 грн. Визначити оптимальну стратегію підприємства, яка дає змогу отримати максимальний гарантований прибуток.
Рішення
Підприємство (гравець A) має дві чисті стратегії: стратегія A1 відповідає розрахунку на теплу погоду і стратегія A2 – на прохолодну. Природу будемо розглядати як гравця B також із двома стратегіями: тепла погода (стратегія B1) і прохолодна (стратегія B2).
Якщо підприємство обере стратегію A1, то у разі теплої погоди (стратегія B1) прибуток становитиме
![]() грн,
грн,
а у разі прохолодної погоди (стратегія B2)
![]() грн.
грн.
Якщо підприємство обере стратегію A2, то у разі теплої погоди (стратегія B1) прибуток становитиме
![]() грн,
грн,
а у разі прохолодної погоди (стратегія B2)
![]() грн.
грн.
Отже, платіжна матриця даної гри має вид:
![]() .
.
|
|
Нижня
ціна гри
Середній виграш гравця A при стратегії B1 гравця B:
|
![]() тому,
що
тому,
що
![]() .
Графік цієї функції
проходить
через точки
.
Графік цієї функції
проходить
через точки
![]() і
і
![]() .
.
Середній
виграш гравця A
при
стратегії B2:
![]() або
або
![]() тому,
що
тому,
що
![]() .
Графік цієї функції
проходить
через точки
.
Графік цієї функції
проходить
через точки
![]() і
і
![]() .
.
Гарантований
середній виграш гравця A
–
мінімум двох
даних
функцій (жирна ламана лінія (рис. 7.2)).
Максимальний гарантований виграш
досягається у точці N
цієї лінії. Точка N
лежить на перетині прямих
![]() і
і
![]() .
Розв’язуючи систему рівнянь цих прямих,
одержуємо
.
Розв’язуючи систему рівнянь цих прямих,
одержуємо
![]() ,
,
![]() .
Таким чином,
.
Таким чином,
![]() ,
,
![]() ;
оптимальна стратегія
;
оптимальна стратегія
![]() ,
ціна гри
,
ціна гри
![]() .
.
Легко розрахувати, яку кількість костюмів і суконь має випускати підприємство при оптимальній стратегії:
![]() костюмів,
костюмів,
![]() суконь.
суконь.
Висновок: оптимальна стратегія підприємства полягає у випуску 812 костюмів і 1260 суконь, що забезпечить йому за будь-якої погоди середній прибуток у сумі 16 965 грн.

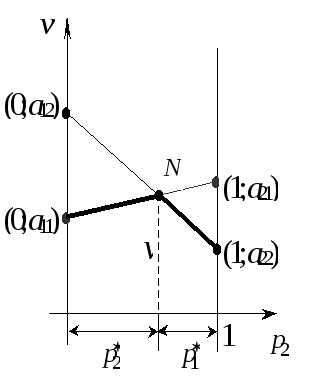 Рис.
7.1
Рис.
7.1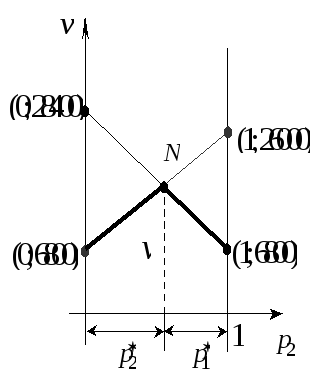 Рис.
7.2
Рис.
7.2