
- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
5.3. Метод потенціалів
Алгоритм знайдення оптимального плану транспортної задачі:
Для даного опорного плану підбираємо потенціали рядків
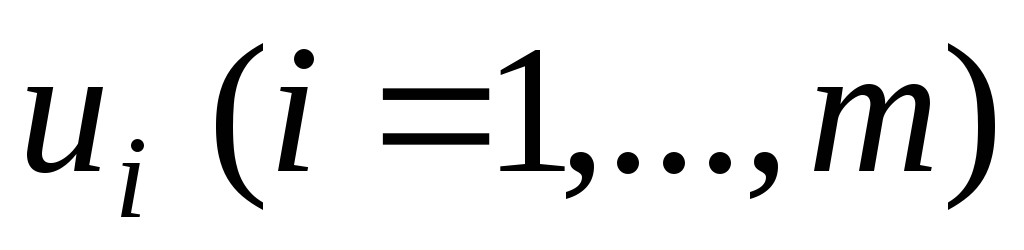 і
потенціали стовпців
і
потенціали стовпців
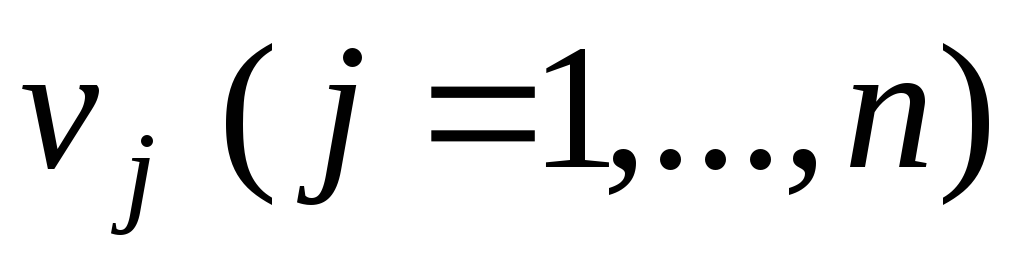 таблиці
постачань так, щоб
для
кожної заповненої клітини
їхня сума дорівнювала відповідній
вартості перевезення одиниці товару
таблиці
постачань так, щоб
для
кожної заповненої клітини
їхня сума дорівнювала відповідній
вартості перевезення одиниці товару
 (числу,
записаному у лівому верхньому куті
клітини):
(числу,
записаному у лівому верхньому куті
клітини):
![]() ,
,
де i – номер рядка, j – номер стовпця, яким належить заповнена клітина. Для визначення потенціалів один з них вважається рівним нулю.
2. Для кожної незаповненої клітини послідовно обчислюємо оцінки
![]() ,
(5.1)
,
(5.1)
де
i
– номер рядка, j
–
номер стовпця, яким належить незаповнена
клітина;
![]() –
потенціали, знайдені в п. 1 алгоритму.
Оцінки для заповнених клітин вважаються
рівними нулю. Складаємо матрицю оцінок.
–
потенціали, знайдені в п. 1 алгоритму.
Оцінки для заповнених клітин вважаються
рівними нулю. Складаємо матрицю оцінок.
3.
Перевіряємо виконання критерію
оптимальності.
Якщо оцінки всіх незаповнених клітин
невід’ємні (![]() ),
то знайдений розподіл є оптимальний –
рішення
закінчене. Якщо серед оцінок незаповнених
клітин є від’ємні, то
будуємо новий
опорний план.
),
то знайдений розподіл є оптимальний –
рішення
закінчене. Якщо серед оцінок незаповнених
клітин є від’ємні, то
будуємо новий
опорний план.
4. Обираємо клітину з найменшою оцінкою для переведення в неї постачання. Для обраної незаповненої клітини будуємо цикл перерахування – зв’язну ламану, одна з вершин якої лежить у незаповненій клітині, інші – у заповнених, а її ланки – уздовж рядків і стовпців таблиці. У вершинах циклу розставляємо знаки “+” і “–” так, щоб у незаповненій клітині стояв знак “+”, а сусідні вершини мали протилежні знаки. Постачання z, що визначається як мінімум серед постачань у клітинах зі знаком “–”, пересуваємо за циклом. У результаті постачання в клітинах циклу зі знаком “+” збільшиться на z, а в клітинах зі знаком “–” зменшиться на z. Клітина, постачання в якій при цьому дорівнюватиме нулю, буде вважатися незаповненою, інші клітини циклу – заповненими. Таким чином одержуємо новий опорний план.
Переходимо до п. 1 алгоритму.
Задача 5.4. Знайти у транспортній задачі 1.3 (с. 10) оптимальний розподіл постачань і мінімальні витрати на перевезення.
Рішення
Почнемо з розподілу постачань, отриманого методом подвійної переваги в задачі 5.3 (див. табл. 5.3). Це пояснюється тим, що даний розподіл виявився ближче (за кількістю необхідних кроків) до оптимального, ніж розподіл, отриманий методом північно-західного кута у задачі 5.2 (див. задачі 5.2 і 5.3).
![]() .
.
З’ясуємо,
чи є цей розподіл оптимальним. Введемо
потенціали
![]() і
і![]() .
Для зручності обчислень потенціали
записуємо праворуч від відповідних
рядків і під відповідними стовпцями
(табл. 5.4). Підберемо ці потенціали так,
щоб для кожної заповненої клітини їхня
сума дорівнювала відповідній вартості
перевезення одиниці товару. Нехай
.
Для зручності обчислень потенціали
записуємо праворуч від відповідних
рядків і під відповідними стовпцями
(табл. 5.4). Підберемо ці потенціали так,
щоб для кожної заповненої клітини їхня
сума дорівнювала відповідній вартості
перевезення одиниці товару. Нехай![]() .
Щоб для заповненої клітини(1,2)
виконувалася рівність
.
Щоб для заповненої клітини(1,2)
виконувалася рівність
![]() ,
потенціал другого стовпця має дорівнювати
1, тобто
,
потенціал другого стовпця має дорівнювати
1, тобто![]() .
Щоб для заповненої клітини(1,3)
виконувалася рівність
.
Щоб для заповненої клітини(1,3)
виконувалася рівність
![]() ,
потенціал третього стовпця має дорівнювати
2, тобто
,
потенціал третього стовпця має дорівнювати
2, тобто![]() .
Щоб для заповненої клітини(2,3)
виконувалася рівність
.
Щоб для заповненої клітини(2,3)
виконувалася рівність
![]() ,
потенціал другого рядка має дорівнювати
1, тобто
,
потенціал другого рядка має дорівнювати
1, тобто![]() .
Аналогічно одержуємо
.
Аналогічно одержуємо![]() ,
,![]() ,
,![]() ,
,![]() .
.
Таблиця 5.4
|
bj ai |
45 |
35 |
55 |
6 | ||||||||
|
40 |
4 |
|
2 |
1 |
|
2 |
|
5 |
|
–
u1
=
0
u1
=
0 | ||
|
|
35 |
5 |
| |||||||||
|
60 |
3 |
|
2 |
|
2 |
3 |
|
7 |
|
0
u2
=
1 | ||
|
|
|
|
| |||||||||
|
90 |
4 |
|
5 |
4 |
|
4 |
5 |
|
2 |
u3
=
3 | ||
|
|
|
25 - |
65 | |||||||||
|
10 |
0 |
|
0 |
0 |
|
–1 |
0 |
|
0 |
|
–
u4
=
– 2 | |
|
|
|
10 |
| |||||||||
v1
=
2
v2
=
1
v3
=
2
v4
=
– 1
Записуємо суму знайдених потенціалів у правому верхньому куті кожної незаповненої клітини (див. табл. 5.4). Користуючись формулою (5.1), обчислює-мо оцінки цих клітин.
Складаємо матрицю оцінок:
 .
.
Оскільки
серед незаповнених клітин таблиці є
клітина (3,1)
з негативною оцінкою, вихідний опорний
план не є оптимальним. Знайдемо новий
опорний план. Побудуємо цикл для клітини
(3,1)
(див.
табл. 5.4). Постачання, що передається в
клітину (3,1):
![]() .
При передачі за циклом 25 одиниць товару
постачання в клітині(3,3)
дорівнюватиме нулю, тому в новому
розподілі ця клітина буде вважатися
незаповненою. Таким чином, приходимо
до нового опорного плану (табл. 5.5).
.
При передачі за циклом 25 одиниць товару
постачання в клітині(3,3)
дорівнюватиме нулю, тому в новому
розподілі ця клітина буде вважатися
незаповненою. Таким чином, приходимо
до нового опорного плану (табл. 5.5).
За допомогою методу потенціалів з’ясуємо, чи є даний опорний план оптимальним. Знайдемо матрицю оцінок.
 .
.
Оскільки оцінки всіх незаповнених клітин невід’ємні, даний опорний план є оптимальний.
Таблиця 5.5
|
bj ai |
45 |
35 |
55 |
6 | |||||||||
|
|
4 |
|
2 |
1 |
|
2 |
|
5 |
|
0 | |||
|
|
35 |
5 |
| ||||||||||
|
60 |
3 |
|
2 |
|
2 |
3 |
|
7 |
|
1 | |||
|
20 |
|
40 |
| ||||||||||
|
90 |
4 |
|
|
4 |
|
3 |
5 |
|
4 |
2 |
| ||
|
25 |
|
|
65 | ||||||||||
|
10 |
0 |
|
0 |
0 |
|
–1 |
0 |
|
0 |
|
–2 | ||
|
|
|
10 |
| ||||||||||
Таким чином, оптимальний розподіл постачань:
 ,
,
мінімальні витрати на перевезення:
![]() .
.
Зауваження 5.2. Транспортна задача завжди має розв’язок. Якщо всі оцінки незаповнених клітин додатні, транспортна задача має єдиний розв’язок. Якщо серед таких оцінок є нульові, то розв’язок не є єдиним. Безліч розв’язків описуємо формулою
![]() ,
,
де другий оптимальний план знаходимо за допомогою перерозподілу постачання в незаповнену клітину з нульовою оцінкою.

 5
5
 45
-
45
- 15
+
15
+ +
+
 5
5 40
40