15. Примеры алгоритмов классификации «метод связности»
Вычисляется мера сходства между всеми объектами:
Ищется максимальная мера сходства:
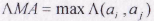
Объекты, между которыми эта мера сходства объединяются в один класс.
На каждом шаге снова ищется максимальная мера сходства, но уже из оставшихся и объединяются объекты, которые связаны этой мерой сходства.
Простейшим классификатором является метод ближнего соседа. Объект присваивается тому классу, который является наиболее распространенным среди соседей данного элемента. Соседи берутся исходя из множества объектов, классы которых уже известны.
16. Примеры практических задач, решаемых с использованием методов корреляционно-регрессионного анализа
Задачи корреляционного анализа:
оценка по выборочным данным величины коэффициента парной корреляции, множественной корреляции, канонической корреляции
проверка значимости выборочных коэффициентов корреляции
оценка степени близости выявленной связи к линейной.
Суть регрессионного метода состоит в построении регрессионной зависимости между искомым параметра - Y и некоторыми другими параметрами X={xi} Задачи регрессионного анализа:
установление формы зависимость у от х
определение вида уравнения регрессии
прогнозирование значений результирующей переменной Y, носящей название отклика по неизвестным значениям
17. Коэффициент корреляции и его свойства.
Определяет количественную оценку линейной связи.
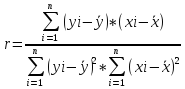
Меняется в пределах -1 ≤ r≤ 1.Знак коэффициента указывает на направление прямое или обратное – взаимосвязи между двумя переменными. Абсолютное значение коэффициента характеризует силу или тесноту рассматриваемой взаимосвязи. Значение r=0 свидетельствует об отсутствии линейной взаимосвязи между рассматриваемыми переменными, нелинейная же связь может иметь место. Коэффициент корреляции равный плюс или минут 1. Указывает на наличие строгой функциональной зависимости. В случае, когда высоким значениям одной переменной соответствуют высокие значения другой переменной, а низким – низкие, то корреляция между переменными положительная. Отрицательная корреляция имеет место там где высоким значениям одной переменной соответствуют низкие значения другой.
18. Способы оценки коэффициентов уравнения регрессии
Графический метод
Метод наименьших квадратов
Суть метода наименьших квадратов заключается в следующем: для каждой из n точек выборки записываются уравнение вида у=ах+b. Затем находятся ошибка еi между расчетным и фактическим значениями. Решение оптимизационной задачи по нахождению таких значений а и b, которые обеспечивают минимальную сумму квадратов ошибок для всех n точек, т.е. решение задачи поиска дает несмещенные и эффективные оценки коэффициентов а и b.