
5. Упругие волны в стержне.
 рисунок
4
рисунок
4
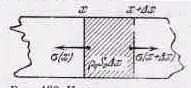
Применим второй
закон Ньютона и закон сложения сил к
движению куска стержня, заключенного
между двумя плоскостями x и х+∆x.
Масса этого куска равна
 ,
,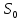 где
где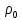 и
и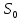 – соответственно плотность и сечение
в отсутствие деформации. Пусть ξ –
смещение центра тяжести рассматриваемого
куска. Тогда
– соответственно плотность и сечение
в отсутствие деформации. Пусть ξ –
смещение центра тяжести рассматриваемого
куска. Тогда
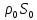 ∆x
∆x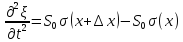
слева стоит
произведение массы куска на ускорение
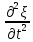 его центра
тяжести, справа – результирующая внешних
сил, действующая на кусок.
его центра
тяжести, справа – результирующая внешних
сил, действующая на кусок.
Разделим уравнение
на
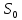 ∆x:
∆x:
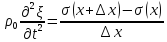 (8)
(8)
Перейдя к пределу
при
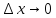 , получим уравнение
, получим уравнение
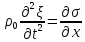 (9)
(9)
справедливое в каждой точке стержня. Оно указывает, что ускорение данной точки пропорционально частной производной напряжения по x в этой точке.
Подставляя в (9) соотношение (8), получим:
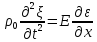 (10)
(10)
Вспомнив теперь формулу, содержащую определение деформации, и подставив ее в (10), получаем:
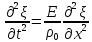 (11)
(11)
Это—волновое уравнение. Оно указывает, что смещение распространяется но стержню в виде волн
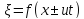 (12)
(12)
или образует суперпозицию таких волн. Скорость распространения этих волн (скорость звука в стержне)
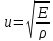 (13)
(13)
(мы опускаем для краткости индекс 0 у ρ). Эта скорость тем больше, чем жестче и чем легче материал. Формула (13)—одна из основных формул акустики.
Наряду со смещением
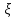 нас интересуют скорость
нас интересуют скорость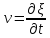 , с которой
, с которой
.движутся отдельные
плоскости
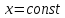 (не
смешивать сu),
деформация ε и напряжение σ. Дифференцируя
(12) по t
и по x,
получаем:
(не
смешивать сu),
деформация ε и напряжение σ. Дифференцируя
(12) по t
и по x,
получаем:
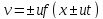 (14a)
(14a)
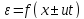 (14б)
(14б)
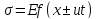 .
(14в)
.
(14в)
Таким образом, смещение, скорость, деформация и напряжение распространяются в виде связанных определенным образом между собой недеформирующихся волн, имеющих одну и ту же скорость и одинаковое направление распространения.
Там, где смещение имеет максимум или минимум, деформация и скорость равны нулю, так как они обе пропорциональны производной
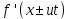 .
Физическая
интерпретация здесь очевидна: около
максимума или минимума смещения соседние
(бесконечно близкие) точки одинаково
смещены и, следовательно, нет ни
растяжения, ни сжатия; в тот момент,
когда смещение достигает максимума
(минимума), его возрастание сменяется
убыванием (или наоборот).
.
Физическая
интерпретация здесь очевидна: около
максимума или минимума смещения соседние
(бесконечно близкие) точки одинаково
смещены и, следовательно, нет ни
растяжения, ни сжатия; в тот момент,
когда смещение достигает максимума
(минимума), его возрастание сменяется
убыванием (или наоборот).
Сравнивая формулы (14а), (14в) и принимая во внимание (13) мы видим, что
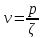 (15)
(15)
Где
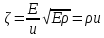 (16)
(16)
есть величина, не
зависящая от вида функции f
и целиком определяемая свойствами
материала. Эта величина называется
удельным акустическим сопротивлением
материала. Она является, как мы видим,
наряду с u
его важнейшей акустической характеристикой.
Название величины
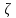 связано с формальной аналогией между
уравнениями (15) и законом Ома (ρ аналогично
разности потенциалов, ν - силе тока).
связано с формальной аналогией между
уравнениями (15) и законом Ома (ρ аналогично
разности потенциалов, ν - силе тока).
Упругие волны в газах и жидкостях
Мы рассматриваем здесь газ или жидкость (так же как твердое тело в предыдущих параграфах) как сплошную непрерывную среду, отвлекаясь от его атомистической структуры. Под смещением мы здесь понимаем общее смещение вещества, заполняющего объем, заключающий в себе очень много атомов, но малый по сравнению с длиной волны.
Будем считать, что рассматриваемый газ или жидкость находятся в очень длинной цилиндрической трубе, образующие которой параллельны оси х, и что смещение зависит только от одной координаты х. Мы можем применить к столбу газа или жидкости, заполняющему трубу, те же рассуждения, что и к стержню. Мы придем, таким образом, к уравнению
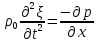 (17)
(17)
где р = - σ
есть давление в газе или жидкости. Здесь
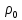 —
значение плотности в состоянии равновесия.
Пусть ей соответствует давление
—
значение плотности в состоянии равновесия.
Пусть ей соответствует давление .
Величины
.
Величины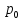 ,
,
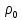 не зависят ни от х, ни от t.
не зависят ни от х, ни от t.
Уравнение (17) применимо и в случае плоских волн в неограниченной жидкой или газообразной среде (можно мысленно выделить цилиндрический столб, параллельный направлению распространения и применить к нему те же рассуждения, что к столбу, заключенному в трубе).
Как известно из термодинамики, р есть функция плотности данной массы газа (или жидкости) и ее температуры. Температура в свою очередь изменяется при сжатии и разрежении. Теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями. В термодинамике показывается, что в этом случае (если можно пренебречь внутренним трением и некоторыми другими явлениями) температура является однозначной функцией плотности, и, следовательно, давление также.
При заданной деформации ε в твердом теле также зависит от температуры. Но в акустике твердых тел это обстоятельство не играет существенной роли.
В газах и в жидкостях за некоторыми исключениями (например вода, при температуре ниже 4° С) температура растет при сжатии и уменьшается при расширении.
Есть однозначная функция плотности:
p=f(p). (18)
Введем обозначения
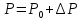 ,
, (19),
(19),
Где
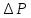 и
и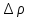 - соответственно изменения давления и
плотности при нарушении равновесия.
- соответственно изменения давления и
плотности при нарушении равновесия.
Подставляя первую формулу (19) в (17) и принимая во внимание, что при равновесии давление не зависит от х, т. е.
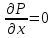
получаем:
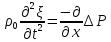 (20)
(20)
Найдем теперь
связь между
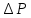 и деформацией ε =
и деформацией ε =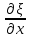 . Мы сначала выразим
. Мы сначала выразим через
через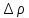 ,
а затем
,
а затем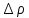 через ε:
через ε:
а) Подставляя (19) в (18), имеем:
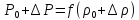
разлагая f(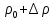 )
в ряд по степеням
)
в ряд по степеням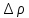 ,
,

Так как
 =
=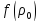 ,
то получаем:
,
то получаем:
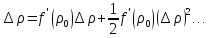 (21)
(21)
Здесь мы сделаем
существенное предположение: будем
считать уплотнения и разрежения настолько
малыми, что допустимо пренебречь в
разложении (21) членами, пропорциональными
 ,
,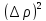 ,
,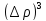 …
и заменить (21) линейным соотношением
…
и заменить (21) линейным соотношением
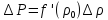
Тем самым мы ограничиваем себя исследованием волн малой интенсивности.
 —постоянный при
данных условиях опыта коэффициент,
определяемый состоянием среды при
равновесии.
—постоянный при
данных условиях опыта коэффициент,
определяемый состоянием среды при
равновесии.
б) Объем
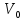 в результате деформации превращается
в объем
в результате деформации превращается
в объем
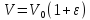 (22)
(22)
так как здесь
поперечный размер (в отличие от твердого
стержня) остается, постоянным, а длина
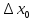 превращается в
превращается в .
Но произведение плотности на объем,
равное массе рассматриваемой порции
вещества, не меняется:
.
Но произведение плотности на объем,
равное массе рассматриваемой порции
вещества, не меняется:
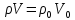
Подставляя (19) и (22), получаем:
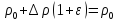
Пренебрегая и
здесь высшими степенями малой величины
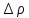 ,
получаем:
,
получаем:
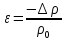 ,
,
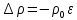
Таким образом,
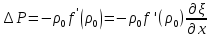 (23)
(23)
Подставляя, наконец, (2.22) в (2.19), мы получаем волновое уравнение
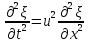 (24),
(24),
Где
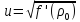 .
(25)
.
(25)
Отсюда заключаем,
что рассматриваемые малые деформации
распространяются в виде плоских не
деформирующихся волн; скорость
распространения (скорость звука) тем
больше, чем сильное в данной среде
возрастает давление при адиабатическом
возрастании плотности; она равна
квадратному корню из производной
давления по плотности, взятой при
значении последней в отсутствие волны
(ρ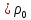 ).
).
Случай идеального газа.
Идеальным газом называется газ, для которого справедливо уравнение состояния
 (26)
(26)
где p – давление, V—объем одного моля, R—универсальная газовая постоянная, T—температура, измеренная по термодинамической шкале («абсолютная температура»), или
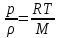
где М— масса 1 моля, ρ= M/V— плотность.
Воздух, кислород, азот, водород и многие другие газы при комнатной температуре и давлении порядка атмосферного можно рассматривать с достаточным для акустики приближением как идеальные газы.
Как учит термодинамика, в случае идеального газа соотношение (2.17) имеет вид:
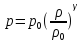 (27)
(27)
Где
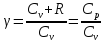
постоянная величина
(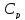 и
и — теплоемкости газа соответственно
при постоянном давлении и постоянном
объеме). Следовательно, здесь
— теплоемкости газа соответственно
при постоянном давлении и постоянном
объеме). Следовательно, здесь
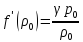 ,
,
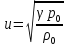 (28)
(28)
Еще задолго до Пуассона вопросом о скорости звука в воздухе занимался Ньютон. Он считал, что
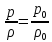 (27а)
(27а)
т. е. не учитывал изменения температуры воздуха при распространении в нем звуковой волны, вследствие чего получил для скорости звука соотношение
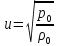 (28а)
(28а)
Это соотношение можно получить из уравнения (25), подставляя в него (27а) вместо (27).
Количественно-качественное сравнение теорий Ньютона и Пуассона
Произведем сравнение результатов, полученных путем применения формул (28) и (28а) – уравнений Ньютона и Пуассона.
Подсчитаем для воздуха:
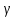 =1,4; ρ = 1,29
при комнатной температуре (20° С, Т =293
К) формула Ньютона дает u =290 м/сек, формула
Пуассона u=331 м/сек. Формула Пуассона
хорошо подтверждается на опыте и для
других газов (но крайней мере при не
очень высоких частотах):
=1,4; ρ = 1,29
при комнатной температуре (20° С, Т =293
К) формула Ньютона дает u =290 м/сек, формула
Пуассона u=331 м/сек. Формула Пуассона
хорошо подтверждается на опыте и для
других газов (но крайней мере при не
очень высоких частотах):
1)для гелия
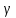 =1,7; ρ =0,179
при температуре 0°C, Т=273 К, давление
=1,7; ρ =0,179
при температуре 0°C, Т=273 К, давление
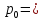 101 325
Па
101 325
Па
формула Ньютона: u = 752 м/сек
формула Пуассона: u=980 м/сек
2)для аммиака
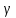 =1,3; ρ =0,77
при температуре 0°C, Т=273 К, давление
=1,3; ρ =0,77
при температуре 0°C, Т=273 К, давление
 101 325
Па
101 325
Па
формула Ньютона: u = 362 м/сек
формула Пуассона: u=413 м/сек
3)для углекислого газа
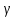 =1,2; ρ =1,98
при температуре 0°C, Т=273 К, давление
=1,2; ρ =1,98
при температуре 0°C, Т=273 К, давление
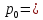 101 325
Па
101 325
Па
формула Ньютона: u = 226 м/сек
формула Пуассона: u=250 м/сек
Этим оправдывается предположение о том, что сжатие и разрежение газа в звуковой волне являются практически адиабатическими процессами.
Как видно из результатов, полученные значения скорости звука из разных формул в одном случае небольшая (для углекислого газа всего 24 м/с), а в другом случае довольно значительная (для гелия она составляет 228 м/с).
Это происходит потому, что количество степеней свободы этих газов различно.
Так как
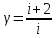 ,
где i-количество
степеней свободы молекул газа
,
где i-количество
степеней свободы молекул газа
Для одноатомного идеального газа (гелий) i=3, т.е.
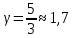
Отсюда и большая разница в расчетах при использовании двух разных формул, чем, например, для кислорода двухатомного газа (i=5):
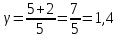
То есть квадратный корень из 1,7 будет больше, чем из 1,4. Соответственно, чем большим количеством степеней свободы обладает газ, тем меньше разница, полученная при расчетах по разным формулам.
Вывод
1) Исследовано распространение упругих волн в средах;
2)В ходе работы было выяснено, что теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями;
3)Произведена количественно-качественное сравнение теорий Ньютона и Пуассона о распространении упругих волн в среде. Сравнение теоретических расчетов и экспериментальных данных показало, что теория Пуассона о том, что распространение упругих волн происходит адиабатно, лучше описывает реальные условия, чем теория Ньютона.
Эта разница тем больше заметна, чем меньше степеней свободы у рассматриваемого газа. Чем сложнее газ, тем меньшую разницу дают расчеты по формулам Ньютона и Пуассона.
