МИНОБРНАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» ФИЛИАЛ В Г.КОГАЛЫМЕ

Доклад на тему:

« Критерии симметрии»

Подготовила: Пилат А.

Студентка 3-го курса

Группа: ЭДНб-11

Проверила: Осинцева М.А.

Когалым 2014

Критерии симметрии:

Статистический критерий для проверки гипотезы H₀, согласно которой одномерная плотность вероятностисимметрична относительно нуля.

Пусть проверяется гипотеза симметрии H₀, согласно которой плотностьвероятности р(х)вероятностного закона, которому подчиняются независимые случайные величины X₁,. . ., Х _n, симметрична относительно нуля, то есть р(х)=р( -х )для любого х из области определения плотности р(х). Любой статистический критерий, предназначенный для проверки Н ₀, называется критерием симметрии.

Наиболее часто в качестве альтернативы к Н ₀ рассматривается гипотеза H₁, согласно которой все рассматриваемые случайные величины Х ₁, . . ., Х _п имеют плотность вероятности Р(х-∆),∆ не =0 . Иначе говоря, согласно гипотезе Н ₁ плотность вероятности случайной величины Х _i получается в результате сдвига плотности р(х)вдоль оси Ох на расстояние вправо или влево, в зависимости от знака D. Если знак смещения D известен, то конкурирующая гипотеза Н₁ наз. односторонней, в противном случае - двусторонней. Простой пример С. к. дает знаков критерий.

С . к. является частным случаем рандомизации критерия.

Статистический критерий:

Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.

Пусть даны выборка х=(х1,…,хn) из неизвестного совместного распределения , и семейство статистических гипотезHo,H1,…. Тогда статистическим критерием называется функция, устанавливающая соответствие между наблюдаемыми величинами и возможными гипотезами:

.

Таким образом каждой реализации выборки x=(x1,…xn) статистический критерий сопоставляет наиболее подходящую с точки зрения этого критерия гипотезу о распределении, породившем данную реализацию.

Виды критериев:

Статистические критерии подразделяются на следующие категории:

• Критерии значимости. Проверка на значимость предполагает проверку гипотезы о численных значениях известного закона распределения: Ho: а=ао — нулевая гипотеза. 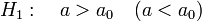или— конкурирующая гипотеза.

• Критерии согласия. Проверка на согласие подразумевает проверку предположения о том, что исследуемая случайная величина подчиняется предполагаемому закону. Критерии согласия можно также воспринимать, как критерии значимости. Критериями согласия являются:

Критерий Пирсона:

Критерий согласия Пирсона , или критерий согласия Х^2(Хи-квадрат) — наиболее часто употребляемый критерийдля проверки гипотезы о принадлежности наблюдаемой выборкиX1,X2,…Xn,объёмом n некоторому теоретическому закону распределенияF( x, O).

Критерий может использоваться при проверке простых гипотез вида

Ho:Fn(x)=F(x,O).

где известныйвектор параметров теоретического закона, и при проверке сложных гипотез вида

,

когда оценка скалярного или векторного параметра распределенияF(x,O) вычисляется по той же самой выборке.