5. Структурные схемы линейных Сау и их преобразования.

Система состоит из элементов которые соединяются последовательно, параллельно или с помощью обратной связи. Каждый элемент имеет 1 вход и 1 выход и заданную ПФ.

Есть правила, которые позволяют по отдельным ПФ элементов получить ПФ всей системы.

1. При последовательном соединении ПФ перемножаются

2. При параллельном суммируются

3. При обратной связи могут быть две ситуации:

1)обратная связь может быть“–“

2) Если обратная связь “+“, то

Пусть нам задана в общем виде структура САР:

По управлению:

По возмущению:

По ошибке:

6. Системные характеристики сау (временная, переходная, импульсная).

Временные характеристики САУ:

1. Переходная характеристика

2. Импульсная – переходная характеристика

Графическое представление этих функций называется временными характеристиками, процессы, проходящие в динамических и статических режимах.

Переходной функцией H(t) – называется функция описывающая сигнал на выходе, при условии, что на вход подана единичное ступенчатое воздействие при нулевых начальных условиях. График H(t) называется переходной характеристикой.

Весовой (импульсной) функцией W(t) называют функцию описывающую реакцию на единичное импульсное воздействие при нулевых начальных условиях. График называется импульсной характеристикой. Аналитическое определение переходных функций и характеристик основано на следующих положениях:

1. Если задана переходная функция системы или звена и известен входной сигнал х(t), то выходной сигнал y(t)будет определяться как: . Изображение выходного сигнала – это произведение изображения входного сигнала на переходную функцию. Сигнал y(t) можно получить как обратное преобразование Лапласа для простых звеньев.

изображение L{y(t)}	оригинал f(t)
1	б(t)
1/s	1(t)
1/s^2	t(t)
1/TS+1	(1/T)е^-t/T
1/S(TS+1)	1-е^-t/T
1/(T^2)(S^2)+1	(1/T)sin(1/T)t

Где Т- постоянная времени.

Так как изображение единичного ступенчатого воздействия равно 1/S, то изображение переходной функции определяется соотношением:.

Для нахождения переходной функции необходимо передаточную функцию разделить на S и выполнить преобразование Лапласа(переход от изображения к оригиналу).

(изображение единичного импульса =1, тогда)Изображение импульсной функции:. ( переходная ф. явл. Изображением импульсной ф.)

;

Две рассмотренные характеристики являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.

7. Системный характеристики Сау(частотная, передаточная)

Частотные характеристики (ЧХ) могут быть получены экспериментально и аналитически.

Если задана ПФ W(S), то путем подстановки получаем частотную ПФкоторая является комплексным выражением состоящим из действительной частии мнимой

Показательная форма частотной ПФ (ЧПФ):

Функция 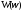, представленная при изменении частоты от нуля до бесконечности получила название АЧХ.

Функция , полученная таким же образом, называется ФЧХ.

ЧПФ можно представить на комплексной плоскости, в этом случае для каждой из частот в диапазоне от нуля до бесконечности производится определение вектора на комплексной плоскости и строится годограф вектора. Годограф будет представлять собой АФЧХ.

Для определенной частоты имеем вектор на комплексной плоскости который характеризуется модулем и аргументом.

Модуль – отношение амплитуды выходного гармонического сигнала к амплитуде входного.

Аргумент – сдвиг по фазе выходного сигнала по отношению к входному.

При этом “–” фазовый сдвиг отображается вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси и наоборот.

Для упрощения графического представления ЧХ используются логарифмические ЧХ: ЛАЧХ и ЛФЧХ.

На шкале частот вместо откладывают lg() и единицой измерения является декада – интервал частот, соответствующий изменению частоты в 10 раз.

На оси ординат при построении ЛАЧХ единицей измерения является децибел.