2. Виды задающих и возмущающих воздействий. Методика расчета характеристик линейных стационарных Сау.

Они представляют собой непрерывные функции времени с различными значениями изменения.

В качестве типовых используют воздействия полиномиального вида:

, где n=0,1,2… ; f_n – постоянные величины; 1(t) – единичная ступенчатая функция. 1(t) = 0, при t<0 и 1(t)=1, при t>=0.

При n=0 полиномиальное выражение определяет ступенчатое воздействие:

При n=1 получим меньшее значение с постоянной скоростью:

При n=2

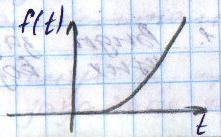
Единичная дельта функция (единичный импульс) – представляет собой математическую идеализацию импульса бесконечно малой длительности и бесконечно большой амплитуды и имеющего конечную площадь равную 1.

Связь между и 1(t):

Гармонически типовые воздействия: , где

k-const, - частота,- фаза.

3. Математическое описание сау. Основы теории преобразования Лапласа.

Поведение САУ в процессе функционирования представляет собой сочетание статистических и динамических режимов. Для проведения теоритических исследований необходимо иметь уравнение, описывающее поведение отдельных элементов при изменяющихся внешних воздействиях. Эти выражения в математической форме – соотношение, связывающее входной и выходной сигналы и воздействия. С целью упрощения математического отношения вводим допущение:

• САУ и ее элементы обладают свойством стационарности.

• Элементы САУ являются линейными.

• Протекающие процессы являются линейными функциями времени, при выполнении нулевых начальных условий.

Рисунок 1 САУ - обобщенный вид.

Действие непрерывной линейной САУ описывается (не)?однородным дифференциальным уравнением:

(1)

А, б, С – постоянные координаты, зависящие от параметров системы

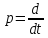- Оператор дифференцирования

Операторный вид дифференциального уравнения

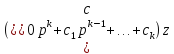()x=(2)

- полином при y - Собственный оператор Q(t)

- полином при x - Оператор управляющего воздействия R1(p)

- полином при z - Оператор возмущающего воздействия R2(p)

(3)

Если рассмотрим только установившийся режим, то 2 принимает вид: (4)

Уравнение 2 описывает как динамику так и статику САУ, а 4 – только статику.

Операторный вид дифф/ уравнение 2го порядка: (5)

(6)

- Постоянные времени; – (безразмерный коэффициент)

Q(p)- Принимает вид алгебраического уравнения:

(Оператор Р – оператор преобразования Лапласа.)

Для линейных дифференциальных уравнений с постоянными параметрами при нулевых начальных условиях с точностью до обозначения оператор P соответствует оператору S: P≡S. Это обстоятельство позволяет использовать для решения 1 интегральное преобразование Лапласа:

(Отображение функции f(t): ) ; f(t)- оригинал; f(s) - изображение

Обратное преобразование Лапласа:

4. Передаточные функции.

Передаточная функция (ПФ) является моделью САР, т.к. полностью характеризует динамические свойства системы.

ПФ – представляет собой отношение изображения по выходной величине Y(S) к изображению входной величине Х(S).

Учитывая , можно для линейной системы записать уравнение в вида:

Q(S)*Y(S)= R₁(S)*X(S)+R₂(S)*Z(S)

Поскольку для линейной системы можно применить принцип наложения, то будет справедливо выделить 2 случая:

1. z(S)=0

Q(S)*Y(S)=R₁(S)*X(S)

2. x(S)=0

Q(S)*Y(S)=R₂(S)*Z(S)

Тогда для любой САР, имеющей входы по управлению и возмущению можно записать:

ПФ по управлению:

ПФ по возмущению:

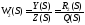
Так как

Тогда

;

Для физической реализации системы необходимо, чтобы выполнялось условие: n>m; n>k.