
Работа № 9. Скважина в ограниченном пласте.
Теоретическая часть.
Ограниченный в плане пласт отличается от полуограниченного наличием двух и более границ. В данной лабораторной работе рассматривается действие скважины при установившемся режиме фильтрации. Для обеспечения данного режима минимум одна из границ должна быть контуром питания (H=const). Расчет понижения уровня воды в скважине производится по формуле Дюпюи (работа № 7). Расчетные формулы радиуса влияния скважины получаются методом зеркальных отображений для каждой конкретной схемы положения границ.
Рассмотрим
четыре схемы расположения скважины
относительно границ пласта, для которых
известны решения для радиуса влияния
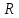 .
.
1)
Пласт-квадрант с двумя контурами питания,
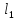 и
и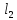 – расстояния от скважины до контуров:
– расстояния от скважины до контуров: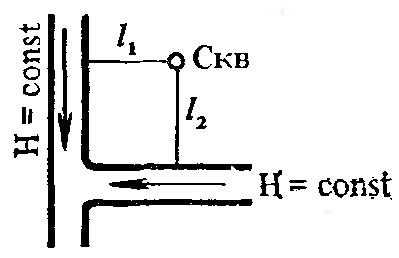
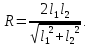
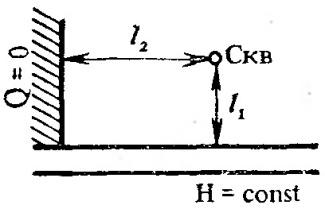
2)
Пласт-квадрант с контуром питания
(расстояние до него
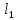 )
и непроницаемым экраном (Q=0,
расстояние
)
и непроницаемым экраном (Q=0,
расстояние
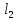 ):
):
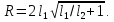
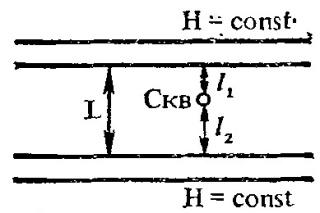
3) Пласт-полоса с двумя контурами питания:
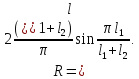
4)
Пласт-полоса с контуром питания
(расстояние до него
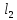 )
и непроницаемым экраном (расстояние
)
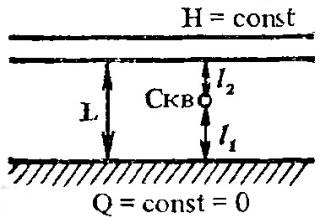
и непроницаемым экраном (расстояние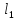 ):
):
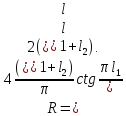
Варианты задач.
Скважина
работает в ограниченном пласте, в
условиях одной из четырех схем,
представленных в теоретической части.
Заданы расстояния
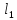 и
и
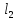 (м)до
границ пласта. Значения необходимых
параметров задачи (
(м)до
границ пласта. Значения необходимых
параметров задачи (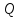 ,
k,
,
k,
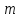 ,
,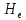 ,
,
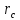 )
взять из лабораторной работы № 7. В
скважине зафиксировано понижение
)
взять из лабораторной работы № 7. В
скважине зафиксировано понижение
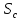 (м)
уровня воды в условиях стационарной
фильтрации.
(м)
уровня воды в условиях стационарной
фильтрации.
Определить
схему расположения границ пласта,
наиболее соответствующую параметрам
задачи. Уточнить величину
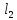 (записать
как
(записать
как
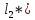 ),
при которой в рамках выбранной схемы
расчетное и наблюдаемое понижения будут
равны друг другу.
),
при которой в рамках выбранной схемы
расчетное и наблюдаемое понижения будут
равны друг другу.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
95 |
170 |
100 |
60 |
330 |
50 |
70 |
245 |
|
|
25 |
140 |
120 |
87 |
65 |
215 |
70 |
105 |
|
|
1.43 |
5.00 |
6.85 |
10.65 |
0.75 |
0.77 |
3.35 |
11.94 |
|
|
|
|
|
|
|
|
|
|
|
Вариант |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
620 |
45 |
88 |
200 |
77 |
150 |
90 |
35 |
|
|
345 |
40 |
99 |
60 |
167 |
55 |
145 |
70 |
|
|
1.61 |
8.00 |
6.32 |
1.35 |
3.90 |
24.10 |
7.40 |
6.70 |
|
|
|
|
|
|
|
|
|
|
|
Вариант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
35 |
170 |
65 |
210 |
400 |
60 |
125 |
515 |
|
|
55 |
190 |
115 |
70 |
55 |
140 |
85 |
300 |
|
|
4.60 |
8.30 |
9.05 |
4.08 |
2.62 |
6.35 |
0.79 |
2.82 |
|
|
|
|
|
|
|
|
|
|
Работа № 10. Скважина в неограниченном пласте. Модель Тейса.
Теоретическая часть.
Рассматривается
работа совершенной скважины в
неограниченном в плане, изолированном
в разрезе напорном пласте (схема Тейса).
Расход потока (дебит скважины) постоянный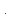 Режим фильтрации –неустановившийся:
напор является функцией расстояния и
времени: H
= f(r,
t)
и лишь на большом удалении от скважины
(в бесконечности) считается постоянным:
Режим фильтрации –неустановившийся:
напор является функцией расстояния и
времени: H
= f(r,
t)
и лишь на большом удалении от скважины
(в бесконечности) считается постоянным:
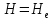 .
.
Общее дифференциальное уравнение радиальной фильтрации имеет вид:
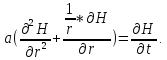
Здесь
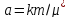 - коэффициент пьезопроводности.
- коэффициент пьезопроводности.
Решение относительно понижения уровня воды в пласте получено Ч. Тейсом:
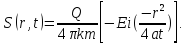
Интегральная
показательная функция
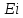 изменяется от
изменяется от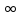 до 0 при изменении аргумента
до 0 при изменении аргумента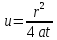 от 0 до
от 0 до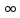 ,
ее значения определяются по таблицам.
,
ее значения определяются по таблицам.
В
начальной стадии характер потока (напор,
скорость, расход) в каждом сечении
интенсивно изменяется – имеет место
ярко выраженная неустановившаяся
фильтрация. В дальнейшем темп снижения
уровня стабилизируется, а воронка
депрессии, увеличиваясь в плане, снижается
параллельно самой себе – наступает
квазистационарный
(квазиустановившийся) режим фильтрации.
Количественно это выражается заменой
функции
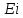 логарифмом:
логарифмом:
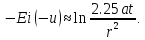
Условие замены (с ошибкой не более 5.7 %): u < 0.1, то есть квазиустановившийся режим наступает при условиях:
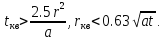
Для этого режима понижение уровня равно
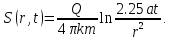
Сравнение данной зависимости с формулой Дюпюи для установившейся фильтрации позволяет ввести понятие приведенного радиуса влияния скважины
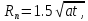
с применением которого формулы полностью совпадают:
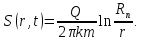
Приведенный
радиус
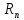 является условной расчетной величиной,
позволяющий вести расчеты неустановившейся
фильтрации по формулам установившейся.
Допускается, что на расстоянии
является условной расчетной величиной,
позволяющий вести расчеты неустановившейся
фильтрации по формулам установившейся.
Допускается, что на расстоянии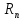 понижение равно нулю, хотя это и не так.
В зоне с радиусом
понижение равно нулю, хотя это и не так.
В зоне с радиусом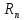 формируется менее 50% расхода скважины,
однако для практических расчетов влияния
скважины принимают именно эту величину,
так как понижение на границе этого
контура составляет менее 1% от понижения
в скважине (приt
> 1000 сут). Анализ показывает (Ф.М.
Бочевер), что влияние скважины
распространяется на расстояние
формируется менее 50% расхода скважины,
однако для практических расчетов влияния
скважины принимают именно эту величину,
так как понижение на границе этого
контура составляет менее 1% от понижения
в скважине (приt
> 1000 сут). Анализ показывает (Ф.М.
Бочевер), что влияние скважины
распространяется на расстояние
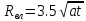 .
.
Пример.
Совершенная
артезианская скважина радиусом 0.1 м
эксплуатируется с дебитом 1450
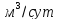 в неограниченном пласте, сложенном
известняками, с параметрами:
в неограниченном пласте, сложенном
известняками, с параметрами: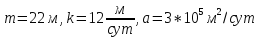 .
.
Определить: величину понижения уровня воды в наблюдательной скважине, расположенной на расстоянии 200 м, через 10 часов от начала работы.
Решение. Делаем проверку на выполнение условий квазистационарной фильтрации:
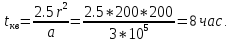
К концу откачки данное условие выполняется. Тогда можно пользоваться формулой:
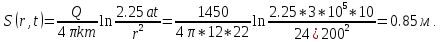
Варианты задач.
Оценивается
понижение
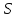 (м)
уровня воды в пласте на расстоянии r
(м) от работающей скважины через время
t
(сут).
Коэффициент пьезопроводности –
(м)
уровня воды в пласте на расстоянии r
(м) от работающей скважины через время
t
(сут).
Коэффициент пьезопроводности –
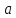 (м2/сут).
Значения дебита
(м2/сут).
Значения дебита
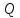 (м3/сут)
и коэффициента водопроводимости
(м3/сут)
и коэффициента водопроводимости
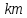 (м2/сут)
взять из работы № 8.
(м2/сут)
взять из работы № 8.
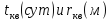 – параметры зоны квазистационарного
режима,
– параметры зоны квазистационарного
режима,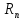 (м) -
приведенный радиус влияния скважины.
Выяснить, наступил ли квазистационарный
режим в точке наблюдения в заданное
время t.
Заполнить пустые ячейки таблицы,
используя формулы теоретической части.
(м) -
приведенный радиус влияния скважины.
Выяснить, наступил ли квазистационарный
режим в точке наблюдения в заданное
время t.
Заполнить пустые ячейки таблицы,
используя формулы теоретической части.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
4*104 |
104 |
106 |
|
|
7*105 |
|
|
|
75 |
|
12 |
|
0.5 |
5.5 |
|
|
|
200 |
400 |
|
|
64 |
|
300 |
|
|
|
1 |
2 |
7.66 |
9.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
581 |
787 |
687 |
|
|
0.83 |
|
0.86 |
|
0.79 |
0.35 |
|
0.33 |
|
Вариант |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
4*105 |
|
|
104 |
3*104 |
5*105 |
2*106 |
7*104 |
|
|
|
9 |
5.9 |
|
|
1.2 |
0.18 |
|
|
|
655 |
|
445 |
|
130 |
|
370 |
|
|
|
|
|
|
|
|
|
|
10.03 |
|
|
|
267 |
459 |
69 |
198 |
|
|
553 |
|
|
1643 |
|
|
|
|
|
|
|
|
|
|
0.48 |
|
1.22 |
|
0.29 |
|
|
|
Вариант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
3*105 |
|
6*104 |
9*103 |
|
3.5*105 |
5.4*104 |
|
|
|
|
0.15 |
|
|
1.5 |
365 |
|
1.2 |
|
|
|
95 |
|
|
700 |
1500 |
770 |
160 |
|
|
0.01 |
|
|
0.04 |
1.225 |
|
|
|
|
|
|
|
598 |
|
|
|
|
359 |
|
|
862 |
486 |
|
|
|
|
|
|
|
|
|
|
0.34 |
0.28 |
|
|
0.35 |
|
Контрольные вопросы.
1) Почему в реальных условиях в неограниченном пласте радиус влияния скважины, достигая определенной величины, далее не увеличивается?
2) Показать аналитически, что при квазистационарном режиме наклон кривой депрессии уровня на заданном расстоянии от скважины постоянен во времени.
3) Показать аналитически, что при квазистационарном режиме скорость снижения уровня не зависит от расстояния.
4) Показать, что разность в понижениях уровня в двух точках пласта в пределах области квазистационарного режима постоянна.
5) Какую часть области депрессии занимает зона квазистационарного режима?
Работа № 11. Связь дебита и понижения по данным откачек.
Теоретическая часть.
Анализ зависимости понижения уровня воды в скважине от ее дебита показывает, что теоретически при установившейся фильтрации данная зависимость линейная для напорных вод и параболическая – для грунтовых. При неустановившейся фильтрации параметры такой связи изменяются во времени (стабилизации не наступает).
На практике при любом режиме фильтрации связь дебита и понижения отличается от теоретической по причине неоднородности пород и сопротивления фильтра. При этом в большинстве случаев понижение уровня нарастает более интенсивно, чем дебит, то есть удельный дебит скважины уменьшается с ростом дебита.
Кривая
зависимости понижения уровня от дебита
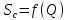 наиболее достоверна по данным откачек.
Реальная кривая обычно представляется
в виде одной из функций:
наиболее достоверна по данным откачек.
Реальная кривая обычно представляется
в виде одной из функций:
 -
парабола:
-
парабола:
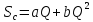 ,
,
-
степенная функция:
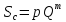 ,
,
-
логарифмическая:
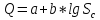 .
.
Для выбора наиболее подходящей функции выполняются следующие действия:
1) проводится откачка минимум с тремя ступенями дебита при установившейся фильтрации (до стабилизации уровня на каждой ступени);
2)
опытные данные (точки) наносятся в
системах координат
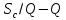 ,
,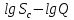 и
и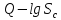 ,
соответствующих вышеназванным функциям.
Для дальнейшего анализа выбирается та
зависимость, в координатах которой
точки наилучшим образом ложатся на
прямую линию;
,
соответствующих вышеназванным функциям.
Для дальнейшего анализа выбирается та
зависимость, в координатах которой
точки наилучшим образом ложатся на
прямую линию;
3) с выбранного графика снимаются параметры прямой линии: точка пересечения прямой с осью ординат и угловой коэффициент, по которым вычисляются необходимые коэффициенты искомой функции (a, b, p, m).
Установленная
связь позволяет делать прогноз понижения
по проектному дебиту или дебита по
понижению (по графику или по формулам).
При этом допускается экстраполяция в
пределах до
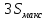 .
.
Пример.
Одиночная
откачка из артезианской скважины
проведена на три ступени:
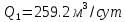 ,
,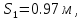
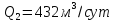 ,
,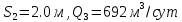 ,
,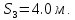
Определить:
характер зависимости дебита от понижения
и понижение уровня при эксплуатации
скважины с проектным дебитом
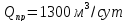 .
.
Решение.
Убеждаемся, что график зависимости
понижения от дебита (в координатах
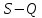 )
не является прямолинейным. Далее строим
графики в координатах, отвечающих
параболе, степенной и логарифмической
функциям:
)
не является прямолинейным. Далее строим
графики в координатах, отвечающих
параболе, степенной и логарифмической
функциям: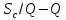 ,
,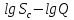 и
и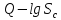 .
Делаем вывод, что в координатах параболы
три точки наилучшим образом ложатся на
прямую линию.
.
Делаем вывод, что в координатах параболы
три точки наилучшим образом ложатся на
прямую линию.
С
графика снимаем значение
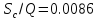 ,
соответствующее проектному дебиту.
Тогда проектное понижение будет равно
,
соответствующее проектному дебиту.
Тогда проектное понижение будет равно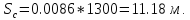 Такое
же решение можно получить по формуле
Такое
же решение можно получить по формуле 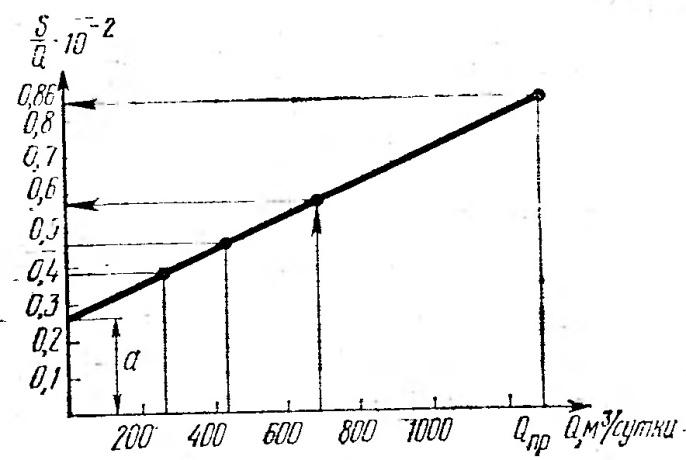
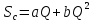 ,
снимая параметры с графика:
,
снимая параметры с графика:
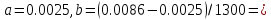
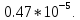 Тогда
Тогда
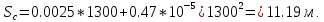
Варианты задач.
Одиночная
откачка из скважины проведена на три
ступени дебита.
Построив график в
координатах
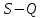 ,
удостовериться, что опытные данные не
ложатся на прямую линию. Отметив точки
на графиках в трех системах координат
,
удостовериться, что опытные данные не
ложатся на прямую линию. Отметив точки
на графиках в трех системах координат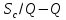 ,
,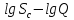 и
и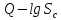 ,
выбрать искомую функцию связи дебита
и понижения. Провести прямую линию и
снять с графика ее параметры. Рассчитать
коэффициенты выбранной функции. Вычислить
прогнозное понижение уровня с учетом
данного проектного дебита.
,
выбрать искомую функцию связи дебита
и понижения. Провести прямую линию и
снять с графика ее параметры. Рассчитать
коэффициенты выбранной функции. Вычислить
прогнозное понижение уровня с учетом
данного проектного дебита.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
165.1 |
106 |
220 |
317 |
523.7 |
421 |
120 |
87 |
|
|
2.99 |
1.12 |
4.42 |
4.55 |
5.46 |
6.87 |
0.52 |
0.49 |
|
|
228.2 |
150 |
355 |
430 |
603.3 |
540 |
375 |
168 |
|
|
4.35 |
2.57 |
10.97 |
6.63 |
8.52 |
9.22 |
3.83 |
1.04 |
|
|
395.3 |
169.3 |
510 |
578 |
684.9 |
822 |
614 |
224 |
|
|
8.23 |
3.70 |
22.08 |
9.57 |
13.44 |
15.13 |
9.65 |
1.47 |
|
|
550 |
190 |
650 |
775 |
765 |
755 |
920 |
500 |
|
|
|
|
|
|
|
|
|
|
|
Вариант |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
116.1 |
337.4 |
512.6 |
211 |
75 |
305 |
100 |
750.4 |
|
|
1.35 |
1.22 |
3.55 |
9.44 |
0.43 |
2.82 |
6.48 |
8.12 |
|
|
144.8 |
518 |
620.3 |
278 |
124 |
356 |
222 |
882.6 |
|
|
1.88 |
2.27 |
7.21 |
13.39 |
0.83 |
3.36 |
17.04 |
12.06 |
|
|
166.4 |
975 |
699 |
325 |
168 |
398 |
376 |
958.7 |
|
|
2.41 |
6.14 |
12.1 |
16.44 |
1.23 |
3.81 |
34.53 |
15.14 |
|
|
260 |
800 |
825 |
450 |
380 |
570 |
600 |
1160 |
|
|
|
|
|
|
|
|
|
|
|
Вариант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
35.5 |
390.8 |
345.5 |
171 |
65.3 |
643.8 |
19.5 |
825.7 |
|
|
1.78 |
2.94 |
1.44 |
3.54 |
0.29 |
3.44 |
0.25 |
5.23 |
|
|
56.8 |
484.9 |
478.5 |
224 |
128.1 |
791.7 |
34 |
978.5 |
|
|
3.60 |
4.76 |
2.48 |
5.06 |
0.67 |
5.81 |
0.50 |
7.91 |
|
|
88 |
623.2 |
612.2 |
408 |
195.8 |
947 |
58 |
1069.4 |
|
|
6.93 |
9.66 |
3.80 |
11.17 |
1.20 |
10.07 |
0.95 |
10.12 |
|
|
170 |
810 |
950 |
660 |
390 |
1210 |
125 |
1450 |
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы.
1) С какой целью определяется функциональная зависимость понижения от дебита?
2) Почему для выбора одной из функций (понижения от дебита) требуется минимум три ступени дебита, а при заданной функции достаточно двух ступеней?
3) В каком случае для прогноза понижения уровня достаточно одной ступени откачки?
4) Каково будет решение задачи, если в координатах «понижение - дебит» опытные данные ложатся на прямую линию?
Работа № 12. Определение гидрогеологических параметров при стационарном режиме фильтрации.
Теоретическая часть.
Будем
рассматривать артезианские скважины,
для грунтовых вод формулы получаются
заменой:
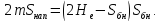
Понижение уровня воды в скважине описывается уравнением Дюпюи:
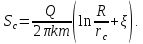
Здесь
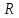 - радиус влияния (при
стационарном режиме – постоянная
величина),
- радиус влияния (при
стационарном режиме – постоянная
величина),
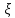 -
показатель несовершенства эксплуатационной
скважины.
-
показатель несовершенства эксплуатационной
скважины.
Имеем
три неизвестных параметра (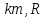 и
и
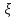 ),
для определения которых требуется еще
минимум две скважины. Рассмотрим кустовую
откачку при двух наблюдательных
скважинах. Для них понижение уровня
запишется в виде (показатель несовершенства
наблюдательных мал, и его можно не
учитывать:
),
для определения которых требуется еще
минимум две скважины. Рассмотрим кустовую
откачку при двух наблюдательных
скважинах. Для них понижение уровня
запишется в виде (показатель несовершенства
наблюдательных мал, и его можно не
учитывать:
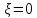 ):
):
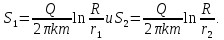
Вычитанием этих формул получаем:
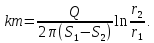
Зная
водопроводимость, можно вычислить
несовершенство опытной скважины. Для
этого запишем формулу для
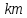 через центральную скважину и одну
наблюдательную:
через центральную скважину и одну
наблюдательную:
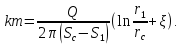
Приравнивая правые части, находим параметр несовершенства:
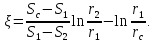
Составная часть величины понижения уровня в центральной скважине, вызванная ее несовершенством вскрытия пласта, определяется по формуле
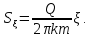
Делением формул находим радиус влияния:
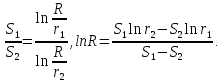
Для
откачки вблизи реки
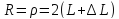 ,
откуда находится
,
откуда находится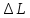 - несовершенство вреза реки (сопротивление
ложа водоема). Для модели Хантуша
вычисляется фактор перетекания
- несовершенство вреза реки (сопротивление
ложа водоема). Для модели Хантуша
вычисляется фактор перетекания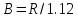 .
.
Пример.
Куст
скважин оборудован на безнапорный пласт
и состоит из центральной (радиусом 0.152
м) и двух наблюдательных, отстоящих от
нее на 25 и 60 м. Мощность пласта 12.5 м. При
откачке с дебитом 600
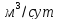 уровень стабилизировался, понизившись
в центральной скважине на 2.5 м, в
наблюдательных – на 0.47 и 0.24 м.
уровень стабилизировался, понизившись
в центральной скважине на 2.5 м, в
наблюдательных – на 0.47 и 0.24 м.
Определить: средний коэффициент фильтрации песков, радиус влияния и несовершенство опытной скважины.
Решение.
Для безнапорного пласта используем
формулы напорного пласта, делая
подстановку
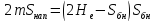 .
Так, для расчета коэффициента фильтрации
по двум наблюдательным формула
.
Так, для расчета коэффициента фильтрации
по двум наблюдательным формула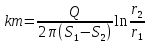 для напорного переходит в такую:
для напорного переходит в такую:
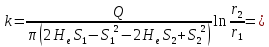
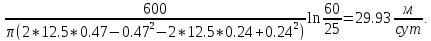
Параметр несовершенства скважины:
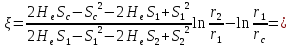
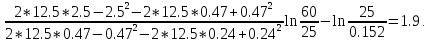
С учетом этого параметра, вычислим коэффициент фильтрации по центральной и первой наблюдательной:
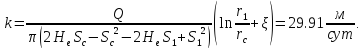
- по центральной и второй наблюдательной:
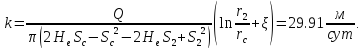
Средний
коэффициент фильтрации равен
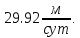
Радиус влияния откачки:
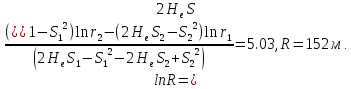
Варианты задач.
Из
напорного водоносного пласта проведена
откачка с дебитом
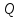 (м3/сут).
К концу опыта понижение уровня
стабилизировалось и составило: в
центральной скважине
(м3/сут).
К концу опыта понижение уровня
стабилизировалось и составило: в
центральной скважине
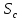 ,
в наблюдательных, расположенных на
расстояниях
,
в наблюдательных, расположенных на
расстояниях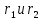 (м) от центральной, соответственно,
(м) от центральной, соответственно,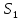 и
и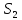 (м).Радиус
возмущающей скважины равен 0.1 м.
(м).Радиус
возмущающей скважины равен 0.1 м.
Используя формулы теоретической части, определить коэффициент водопроводимости пласта и радиус влияния скважины. Вычислить, какую часть (%) от величины понижения в центральной скважине составляют потери напора на фильтре.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1814.4 |
1814.4 |
1814.4 |
1814.4 |
1339.2 |
1339.2 |
1339.2 |
1339.2 |
|
|
47.8 |
47.8 |
120 |
15.9 |
15.9 |
40 |
23.9 |
23.9 |
|
|
120 |
157.2 |
157.2 |
40 |
52.4 |
52.4 |
60 |
78.7 |
|
|
8.93 |
8.93 |
8.93 |
8.90 |
8.93 |
8.93 |
8.90 |
8.93 |
|
|
1.52 |
1.52 |
1.08 |
1.52 |
1.52 |
1.08 |
1.52 |
1.52 |
|
|
1.08 |
0.96 |
0.96 |
1.08 |
0.96 |
0.96 |
1.08 |
0.96 |
|
km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rвл |
|
|
|
|
|
|
|
|
|
Вариант |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
907.2 |
907.2 |
907.2 |
907.2 |
1036.8 |
1036.8 |
1036.8 |
1036.8 |
|
|
60 |
12 |
12 |
30 |
95.6 |
95.6 |
240 |
30.3 |
|
|
78.7 |
30 |
39.5 |
39.5 |
240 |
314.4 |
314.4 |
76.4 |
|
|
8.90 |
8.90 |
8.90 |
8.90 |
8.90 |
8.90 |
8.90 |
8.90 |
|
|
1.08 |
1.52 |
1.52 |
1.08 |
1.52 |
1.52 |
1.08 |
1.52 |
|
|
0.96 |
1.08 |
0.96 |
0.95 |
1.08 |
0.96 |
0.96 |
1.08 |
|
km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rвл |
|
|
|
|
|
|
|
|
|
Вариант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1468.8 |
1468.8 |
1468.8 |
1468.8 |
604.8 |
604.8 |
604.8 |
604.8 |
|
|
30.3 |
76.4 |
57 |
57 |
146.6 |
74.5 |
74.5 |
182.8 |
|
|
97.5 |
97.5 |
146.6 |
188.1 |
188.1 |
182.8 |
238 |
238 |
|
|
8.90 |
8.90 |
8.90 |
8.90 |
8.90 |
8.93 |
8.93 |
8.93 |
|
|
1.52 |
1.08 |
1.42 |
1.49 |
1.08 |
1.52 |
1.52 |
1.08 |
|
|
0.96 |
0.96 |
0.98 |
0.93 |
0.96 |
1.08 |
0.90 |
0.96 |
|
km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rвл |
|
|
|
|
|
|
|
|
Контрольные вопросы.
1) Как оценивается время наступления установившегося режима?
2) Какой способ наиболее надежный для определения несовершенства опытной скважины?
3) Как несовершенство центральной скважины влияет на определение водопроводимости?
4) Почему пьезопроводность не следует находить по центральной скважине?

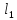
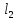
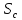
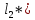
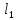
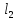
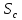
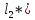
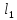
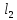
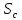
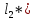
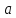
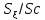 ,%
,%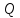
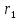
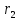
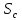
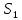
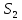
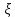
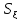
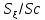 ,%
,%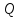
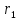
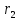
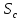
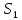
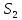
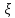
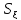
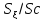 ,%
,%