
- •«Тюменский государственный нефтегазовый университет»
- •Физика, часть 3
- •1.Волновая оптика
- •1.1.Световой вектор. Уравнение плоской световой волны
- •1.2. Интерференция световых волн. Условия, необходимые для осуществления интерференции
- •1.3.Условия максимумов и минимумов при интерференции световых волн
- •1.4.Интерференция в тонких пленках
- •1.5. Кольца Ньютона
- •Контрольные вопросы
- •Дифракция света. Принцип Гюйгенса-Френеля
- •Дифракция от одной щели.
- •Дифракция на одномерной дифракционной решётке
- •Угловая дисперсия и разрешающая способность дифракционной решетки
- •Угловая дисперсия равна:
- •Дифракция рентгеновских лучей на пространственной решетке
- •Поглощение света
- •Поляризация света. Естественный и поляризованный свет
- •Поляризация при отражении и преломлении
- •Двойное лучепpеломление. Поляpизационные пpизмы и поляpоиды. Явление дихpоизма
- •Вpащение плоскости поляpизации. Искуственная оптическая анизотpопия. Эффект Кеppа и его пpименение
- •1.Явления квантовой оптики
- •1.1. Тепловое излучение и его характеристики. Закон Кирхгофа
- •1.2.Законы излучения абсолютно черного тела. Законы Стефана-Больцмана и Вина
- •1.3.Формула Релея-Джинса. Ультрафиолетовая катастрофа. Квантовая гипотеза и формула Планка
- •1.4.Оптическая пирометрия
- •1.5.Квантовая природа света. Фотон и его характеристики.
- •1.6. Виды фотоэффекта. Внешний фотоэффект и его законы.
- •1.7. Эффект Комптона
- •1.8. Коpпускуляpно-волновой дуализм свойств света
- •1.9. Контрольные вопросы и задачи к разделу «Явления квантовой оптики»
- •2.Элементы квантовой механики
- •2.1. Гипотеза де Бройля. Корпускулярно-волновой дуализм микрочастиц
- •Опыты Девиссона и Джермера (1927г.)
- •Опыты Тартаковского и Томсона (1928 г.)
- •2.2. Соотношение неопределенностей
- •Волновая функция
- •Уравнение Шредингера
- •2.5.Задача квантовой механики о движении свободной частицы
- •Задача квантовой механики о частице в одномерной прямоугольной потенциальной яме
- •Понятие о туннельном эффекте
- •1. Автоэлектронная (холодная) эмиссия электронов
- •1.8. Атом водорода в квантовой механике. Квантовые числа
- •Здесь и совпадает с формулой радиуса первой боровской орбиты; численное значение этого параметра равно;a – множитель, который можно определить из условия нормировки волновой функции:
- •2.10. Спин электрона. Принцип Паули
- •2.11. Спектр атома водорода
- •2.12. Распpеделение электpонов в атоме по энеpгетическим состояниям. Пеpиодическая система элементов д.И.Менделеева
- •2.13. Рентгеновское излучение
- •2.14. Поглощение света, спонтанное и вынужденное излучения
- •2.15. Лазеры
- •1. Инверсия населенностей
- •2. 16. Способы создания инверсии населенностей
- •2.17. Положительная обратная связь. Резонатор
- •2.18. Принципиальная схема лазера
- •2.17. Линейный гаpмонический осциллятоp
- •3.6. Понятие о квантовой теории электропроводности металлов
- •3.7. Явление сверхпроводимости. Свойства сверхпроводников
- •Критические температуры перехода для некоторых сверхпроводников
- •4.Зонная теория твёрдых тел
- •4.1. Энергетические зоны электронов в кристалле
- •4.2. Металлы, полупроводники, диэлектрики в зонной теории твёрдых тел
- •4.3.Полупроводники. Собственная проводимость полупроводников
- •4.4. Примесная проводимость полупроводников
- •4.5. Равновесные концентрации носителей заряда в полупроводнике
- •4.6. Зависимость электропроводности полупроводников от температуры
- •Электронно-дырочный переход
- •Внутренний фотоэффект
- •Воздействие излучения на полупроводник. Фоторезистивный эффект
- •Устройство и характеристики фоторезисторов
- •Применение фоторезисторов
- •Фотоэффект в электронно-дырочном переходе. Фото-э.Д.С.
- •Применение вентильного фотоэффекта
- •Биполярный транзистор
- •Состав и характеристики атомного ядра
- •Характеристики атомного ядра
- •Ядерные силы
- •Понятие об обменном характере ядерных сил. Кванты ядерного поля
- •Радиоактивность
- •Ядерные реакции
- •Деление атомных ядер
- •Элементарные частицы
- •2 Кристаллические решетки твердых тел представляют собой периодические структуры и являются естественными трехмерными дифракционными решетками.
Дифракция от одной щели.
Пусть на узкую щель, расположенную в плоской непрозрачной преграде падает нормально плоская монохроматическая световая волна. Ширина щели АВ=b. Поместим за щелью собирательную линзуLи экран в фокальной плоскости линзы (рис.).
В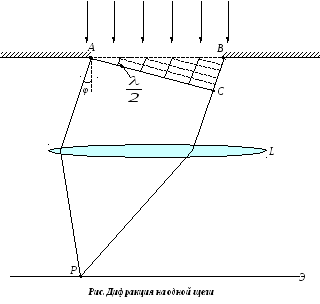 соответствии с принципом Гюйгенса -
Френеля освещённую щель можно рассматривать
как множество точечных когерентных
источников вторичных волн. Вторичные
волны, посылаемые под угломφк
оптической оси линзы, соберутся на
экране в точкеР.
соответствии с принципом Гюйгенса -
Френеля освещённую щель можно рассматривать
как множество точечных когерентных
источников вторичных волн. Вторичные
волны, посылаемые под угломφк
оптической оси линзы, соберутся на
экране в точкеР.
Разобьем щель на зоны Френеля. Для этого
на ВСотложим отрезки, равные половине
длины волны падающего на щель света![]() и проведём через эти точки плоскости,
параллельныеАС.
и проведём через эти точки плоскости,
параллельныеАС.
Эти плоскости разделят щель на зоны
Френеля, которые в этом случае представляют
собой полоски, параллельные краям щели
(рис.). Оптическая разность хода волн,
идущих от соседних зон Френеля равна
![]() .
.
Число зон Френеля Zбудет равно:
 .
()
.
()
Оно зависит от угла
![]() ,
длины волны падающего света и ширины
щели
,
длины волны падающего света и ширины
щели![]() .
.
В направлениях, которым соответствует четное число зон Френеля, имеет место минимум интенсивности света (колебания от каждой пары соседних зон гасят друг друга). Для этих направлений
![]() ,
()
,
()
где
![]() – целое число:m =
1, +2 …
– целое число:m =
1, +2 …
Из выражения () получаем условие дифракционного минимума. Оно имеет вид:
![]() ;m=+1, +2,
+3 … ()
;m=+1, +2,
+3 … ()
В направлениях, которым соответствует нечетное число зон Френеля, (Z=2m+1), наблюдается максимум интенсивности света, так как действие одной зоны остаётся нескомпенсированным.
Условие максимума имеет вид:
![]() ;m=0, +1, +2,
+3 …
;m=0, +1, +2,
+3 …
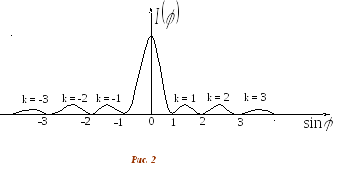
При φ=0все вторичные волны проходят одинаковые оптические пути и интерферируя усиливают друг друга. Максимум, соответствующийφ=0называется главным.
Точный расчёт показывает, что интенсивности максимумов относятся к интенсивности главного максимума Jследующим образом:
1 : 0,045 : 0,016.
Дифракция на одномерной дифракционной решётке
Дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей, разделённых непрозрачными промежутками (рис.)
Щ ель
в и находящуюся рядом с ней непрозрачную
часть называютэлементом решётки.
Ширинаdодного элемента решётки
называетсяпостояннойилипериодомрешетки. Пусть на дифракционную решетку
падает нормально её поверхности плоская
световая волна. Поместим за решёткой
собирательную линзу и экран в фокальной
плоскости линзы (рис.).
ель
в и находящуюся рядом с ней непрозрачную
часть называютэлементом решётки.
Ширинаdодного элемента решётки
называетсяпостояннойилипериодомрешетки. Пусть на дифракционную решетку
падает нормально её поверхности плоская
световая волна. Поместим за решёткой
собирательную линзу и экран в фокальной
плоскости линзы (рис.).
Д ля
направлений, удовлетворяющих условию
ля
направлений, удовлетворяющих условию
![]() ,
каждая щель достигает минимума
интенсивности (сама себя гасит). Условие
минимума для одной щели является условием
главных минимумов для дифракционной
решетки .
,
каждая щель достигает минимума
интенсивности (сама себя гасит). Условие
минимума для одной щели является условием
главных минимумов для дифракционной
решетки .
Рассмотрим сложение волн, приходящих от идентичных точек различных щелей. Разность хода волн, приходящих от двух соседних щелей равна:
![]() .
( )
.
( )
Воспользуемся условием интерференционного
максимума:
![]() .
Если Δ равно целому числу длин волн
(четному числу длин полуволн) , то волны
от всех щелей усиливают друг друга,
будут наблюдаться максимумы интенсивности.
Эти максимумы называютсяглавными.
.
Если Δ равно целому числу длин волн
(четному числу длин полуволн) , то волны
от всех щелей усиливают друг друга,
будут наблюдаться максимумы интенсивности.
Эти максимумы называютсяглавными.
Условие главных максимумов имеет вид:
![]() (m=0, +1,
+2, +3 …).
( )
(m=0, +1,
+2, +3 …).
( )
В направлениях, для которых волны от различных щелей гасят друг друга, наблюдаются добавочные (побочные) минимумы. Пусть число щелей решетки равно N. Расчёт показывает, что между соседними главными максимумами имеетсяN-1добавочный минимум.
Д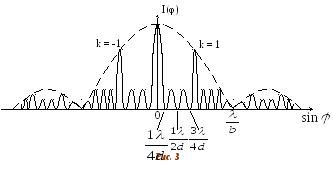 ифракционная
картина, получающаяся от решётки, имеет
вид (рис.) (дляN=4).
ифракционная
картина, получающаяся от решётки, имеет
вид (рис.) (дляN=4).
Из формулы () следует, что положение главных максимумов зависит от длины волны. Это означает, что при пропускании через решётку белого света все максимумы, кроме центрального, разложатся в спектр. Фиолетовая часть спектра обращена к центру картины, красная – наружу (рис.).
 Из
изложенного выше следует, что дифракционная
решетка может быть использована какспектральный прибор1.
Из
изложенного выше следует, что дифракционная
решетка может быть использована какспектральный прибор1.
Дифракционные решетки бывают прозрачными и отражательными. Прозрачные решетки изготавливаются из стекла или кварцевых пластинок, на которые алмазным резцом наносятся штрихи. Отражательные решетки изготавливаются путем нанесения штрихов на поверхность металлического зеркала. Лучшие решетки имеют до 2000 штрихов на мм.
