1.2.Законы излучения абсолютно черного тела. Законы Стефана-Больцмана и Вина

Закон Стефана-Больцмана был экспериментально установлен Стефаном в 1879 г. и теоретически обоснован Больцманом в 1884 г. Запишем выражение для него:

. (1.8 )

Энергетическая светимость абсолютно черного тела пропорциональна четвёртой степени абсолютной температуры.Коэффициент пропорциональностиσназываетсяпостоянной Стефана; она имеет значениеσ = 5,67·10^-8 Вт∙м^-2К^-4.

Так как – величина интегральная, то закон Стефана-Больцмана ничего не говорит о распределении энергии в спектре излучения абсолютно черного тела.

Экспериментальные зависимости спектральной плотности энергетической светимости абсолютно черного тела от частоты νи длины волны излученияλпри различных температурах имеют вид, приведённый на рисунке 1.2 . Площадь под кривыми распределения соответствуют энергетической светимости.

Проведём анализ экспериментальных зависимостей.

1. Энергия излучения абсолютно черного тела распределена неравномерно по спектру. Абсолютно черное тело почти не излучает в области очень малых и очень больших частот.

2. При повышении температуры максимум спектральной плотности энергетической светимости смещается в сторону более высоких частот или более коротких длин волн.

Положение и высота этого максимума определяется законами Вина.

Первый закон Вина (закон смещения).Длина волны, на которую приходится максимум энергии излучения абсолютно чёрного тела, обратно пропорциональна абсолютной температуре:

. ( 1.9)

Здесь b– постоянная Вина (b = 2,9∙10^-3 м∙К).

Второй закон Вина. Максимальное значение спектральной плотности энергетической светимости абсолютно чёрного тела пропорционально пятой степени абсолютной температуры

, (1.10)

где С₁– вторая постоянная Вина (С₁ = 1,29∙10^-5 ).

1.3.Формула Релея-Джинса. Ультрафиолетовая катастрофа. Квантовая гипотеза и формула Планка

Релеем и Джинсом была сделана попытка получить теоретически функцию Кирхгофа на основе классической термодинамики и электродинамики.

Основные идеи при выводе формулы Релея-Джинса заключались в следующем.

1. В замкнутой полости излучение представляет собой систему стоячих электромагнитных волн.

2. Каждой стоячей волне приписывалась средняя энергия.

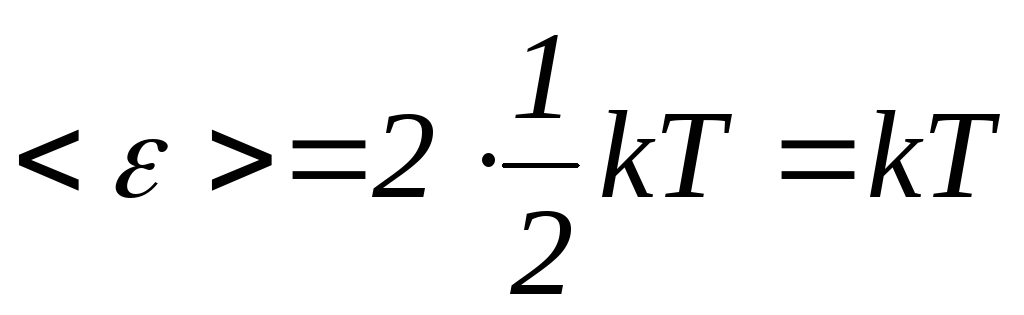3. Подсчитывали число стоячих волн, приходящихся на интервал частот dν.

Для спектральной плотности энергетической светимости абсолютно черного тела была получена формула:

. (1.11)

Сравнение формулы Релея-Джинса с экспериментом дает следующий результат.

1. Формула Релея-Джинса согласуется с экспериментом только в области малых частот (рис.1.3). При.

2. Энергетическая светимость абсолютно черного тела

.

Последние два вывода оказались абсурдными; этот результат получил название «ультрафиолетовая катастрофа», так как вывод формулы с точки зрения классической физики был безупречен.

Правильное выражение для функции Кирхгофа и теоретическое обоснование спектральных закономерностей теплового излучения было дано Максом Планком (1900 г.).

Основные идеи при выводе формулы Планка заключались в следующем.

1. Стенки излучающей полости рассматривались как совокупность линейных гармонических осцилляторов.

2. Энергия атома-осциллятора может принимать лишь определенные дискретные значения (квантовая гипотеза). Эти значения равны целому числу квантов энергии:

.

3. Энергия кванта определяется выражением:

(h = 6,625∙10^-34 Дж∙с).

Для получения формулы Планка возьмем исходное выражение для функции Кирхгофа

, (1.12)

где – средняя энергия атома-осциллятора. Она определится выражением:

, ( 1.13)

где – вероятность того, что атом-осциллятор находится в состоянии с энергией.

По формуле Больцмана эта вероятность равна:

. (1.14)

Из условия нормировки следует, что сумма всех вероятностей равна единице:

. (1.15)

Подставим выражение (1.14 ) в условие нормировки (1.15 ), получим выражение для нормировочного множителя А:

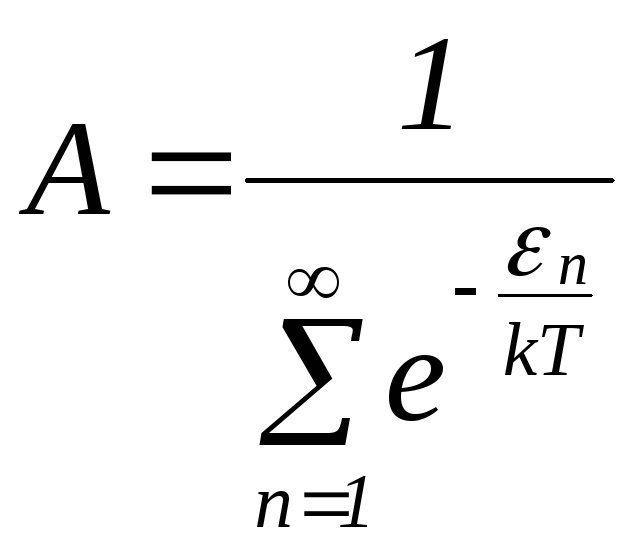и. (1.16)

Тогда 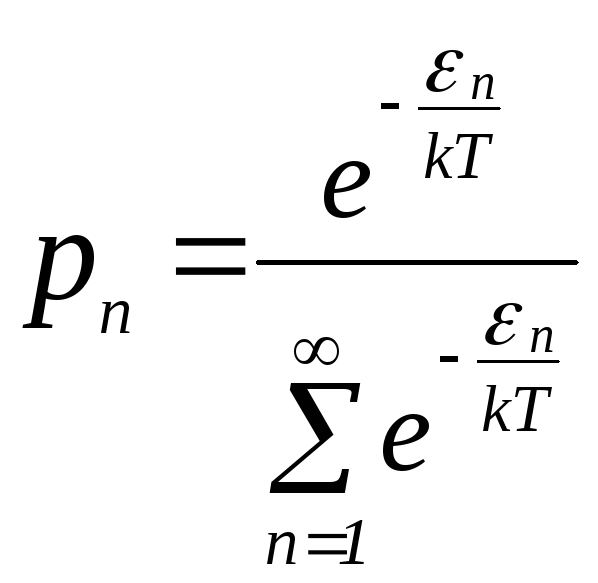, (1.17)

. (1.18)

Подставим выражения (1.17) и (1.18) в формулу для средней энергии осциллятора (1.13), получим:

. (1.19)

Суммирование дает следующий результат:

. (1.21)

Исходя из этих предположений, для спектральной плотности энергетической светимости было получено выражение:

. (1.22)

Так как и, то

. (1.23)