-
Дискретные системы: виды квантования, виды модуляции.
Система автоматического управления называется дискретной, если выходная величина какого – либо ее элемента имеет дискретный характер.
Дискретизация осуществляется путем квантования непрерывного сигнала по времени и по уровню. Это означает, что аналоговый сигнал в ИЭ через равные промежутки T заменяется дискретными по уровню значениями, ближайшими к значениям непрерывного сигнала (рис.8.1).
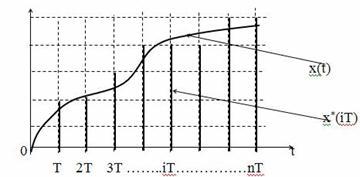
При квантовании по уровню непрерывный сигнал х(t) преобразуется в последовательность дискретных сигналов, фиксированных в произвольные моменты времени при условии x = const.
При квантовании по времени сигналы фиксируются в дискретные моменты времени t = const.
При квантовании по уровню и по времени непрерывный сигнал заменяется дискретными уровнями, ближайшими к значениям непрерывного сигнала в дискретные моменты времени t = const.
Виды импульсной модуляции.
Если каждый квант информации дискретного процесса, квантованного только по времени, передается с помощью импульса при определенном виде модуляции его параметров, то дискретные системы называются импульсными. В итоге различают импульсные системы с амплитудной (АИМ), широтной (ШИМ), фазовой (ФИМ), частотной (ЧИМ) видами модуляции. Кроме того, бывают системы с комбинированными видами модуляции. Если в системах с АИМ амплитуда импульсов пропорциональна значениям квантованного процесса, то такие импульсные системы могут быть линейными. При всех других видах модуляции они относятся к классу нелинейных систем.
-
Преимущества и недостатки дискретных систем.
Достоинства и недостатки дискретных систем. С выхода дискретного элемента информация о входном сигнале поступает лишь в дискретные моменты времени, что приводит к некоторой потере информации. В цифровых системах процессы преобразования сигналов обычно происходят не в реальном масштабе времени, вследствие чего вносится определенное запаздывание. Эти факторы являются причиной понижения точности дискретных САУ. Однако дискретные системы обладают рядом преимуществ перед непрерывными системами:
1.С помощью одной дискретной САУ (автоматического управляющего устройства) можно осуществлять управление процессами в нескольких управляемых объектах поочередным подключением этих объектов к АУУ или обеспечивать управление многими параметрами одного технологического процесса (объекта).
2.Дискретные элементы обеспечивают более высокую точность преобразования и передачи информации.
3.Дискретные системы во многих случаях оказываются проще в конструктивном отношении аналогичных непрерывных систем.
-
Функциональная и алгоритмическая структуры амплитудно-импульсной системы.
В общем случае импульсный элемент может входить в состав любого функционального блока системы управления. Дискретный характер работы системы может быть обусловлен, например, использованием датчика периодического действия (различные анализаторы состава вещества). Но в большинстве случаев дискретность системы связана с наличием в ее контуре коммутирующих устройств МП и ДМП (см. рис. 9.1), которые периодически замыкают и разрывают цепь регулирования.
Рассмотрим типичную функциональную структуру импульсной системы (рис. 9.3, а). К такой структуре могут быть сведены почти все случаи включения импульсного элемента. Импульсные элементы и , которые реально находятся в задатчике и обратной связи, могут быть учтены одним импульсным элементом .
Импульсный элемент , осуществляющий в системе квантование по времени, можно рассматривать как амплитудно-импульсный модулятор (рис. 9.4, а). Модулятор умножает несущий сигнал – последовательность одинаковых импульсов, поступающих с генератора импульсов , на модулирующий сигнал – входной непрерывный сигнал . Образующийся при
Рис. 9.3. Структуры амплитудно-импульсной системы управления
этом на выходе дискретный сигнал представляет собой последовательность импульсов, амплитуды которых равны или пропорциональны мгновенным значениям непрерывного сигнала.
Для упрощения анализа системы с АИМ целесообразно реальный импульсный элемент заменить эквивалентным последовательным соединением идеального импульсного элемента и формирующего элемента (рис. 9.4, б). Идеальный импульсный элемент преобразует непрерывный сигнал в последовательность мгновенных равностоящих друг от друга импульсов, площади которых равны значениям входного сигнала в дискретные моменты времени. Формирующий элемент или демодулятор образует из мгновенных импульсов такие импульсы, которые по форме совпадают с импульсами на выходе реального импульсного элемента.
Реакция формирующего элемента на единичный импульс, т. е. на дельта-функцию, есть не что иное, как весовая функция этого элемента.
Поэтому, согласно известному соотношению, передаточная функция формирующего элемента , (9.4)
где – функция, описывающая импульс на выходе реального импульсного элемента при действии на входе дельта-функции.
Формирующий элемент является звеном непрерывного действия и его при анализе удобно объединять с непрерывной частью системы (рис. 9.3, б). Образующееся при этом соединение называется приведенной непрерывной частью системы. Передаточная функция приведенной непрерывной части . (9.5)
Рис. 9.4. Алгоритмическая структура импульсного элемента