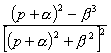Основные свойства (теоремы) преобразования Лапласа
1.
Линейность преобразования.Для любых постоянных
и
.
(2.8)
2.
Дифференцирование оригинала.
Если производная
является
функцией-оригиналом, т.е. обладает
указанными тремя свойствами, то
,
где
=
,
.
И вообще, еслиn-я
производная
является
функцией-оригиналом, то
,
где
,k=0,1,…n-1.
Если начальные условия нулевые, т.е.
,
то последняя формула принимает вид:
.
(2.9)
В таблице приведены выражения изображения Лапласа для некоторых типовых сигналов.
Изображения по Лапласу типовых сигналов
|
Оригинал
|
Изображение
|
Оригинал
|
Изображение
|
|
δ(t) |
1 |
|
|
|
1(t) |
|
sin( |
|
|
|
|
cos( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)
)
Прямые показатели качества
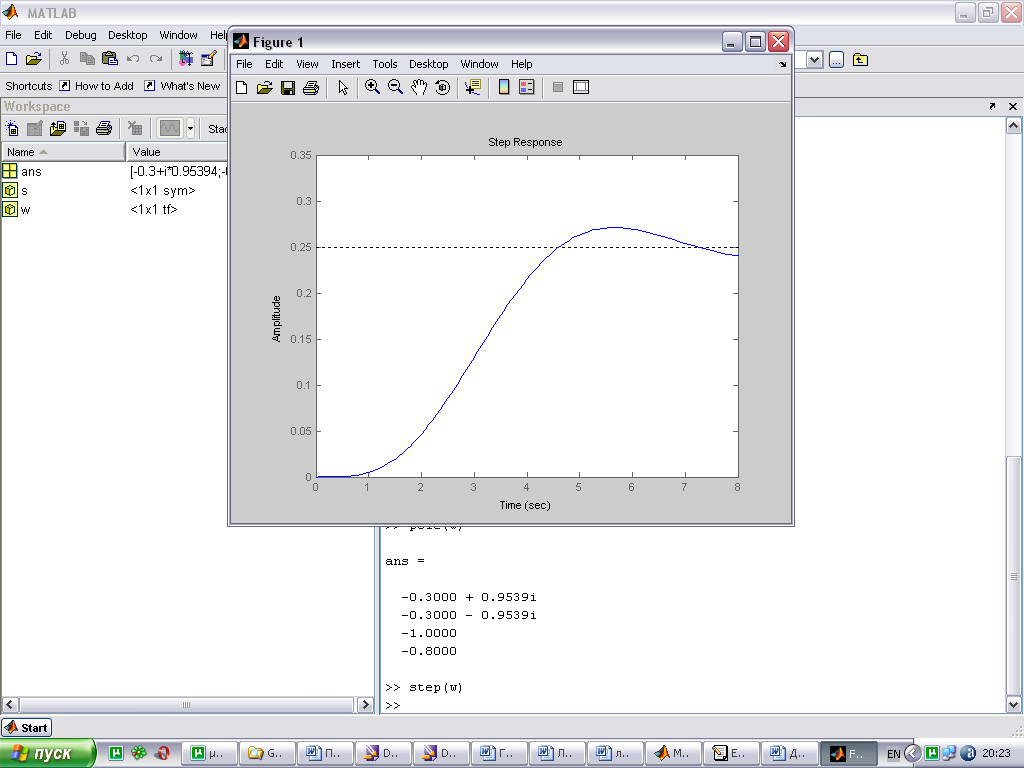
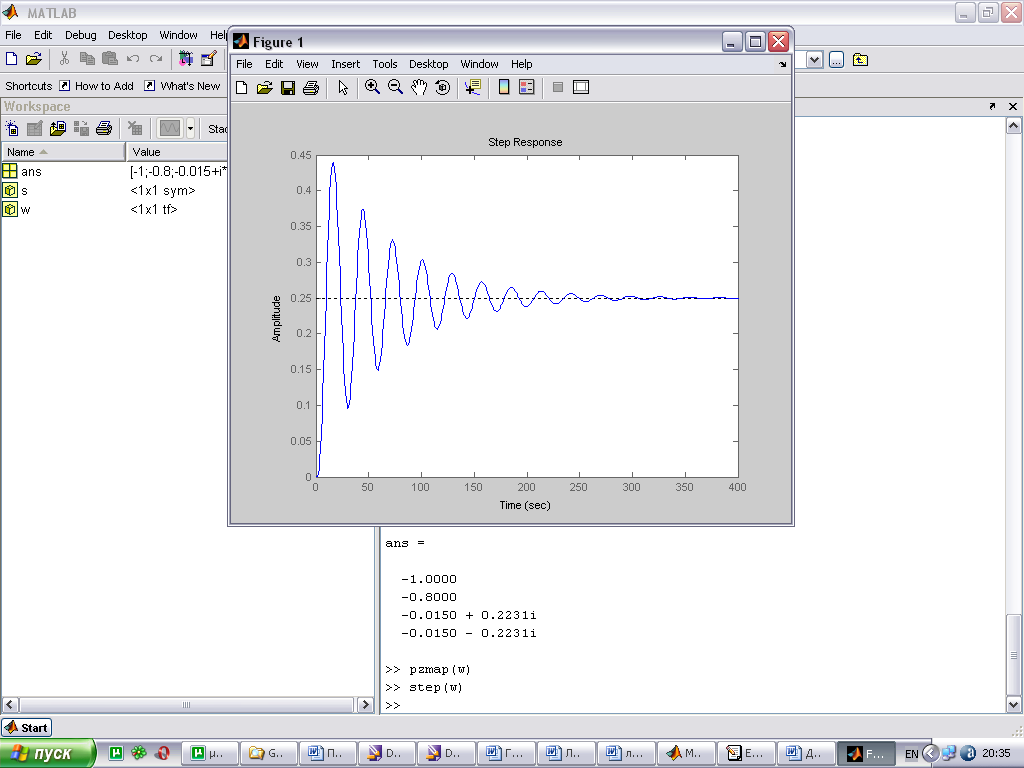
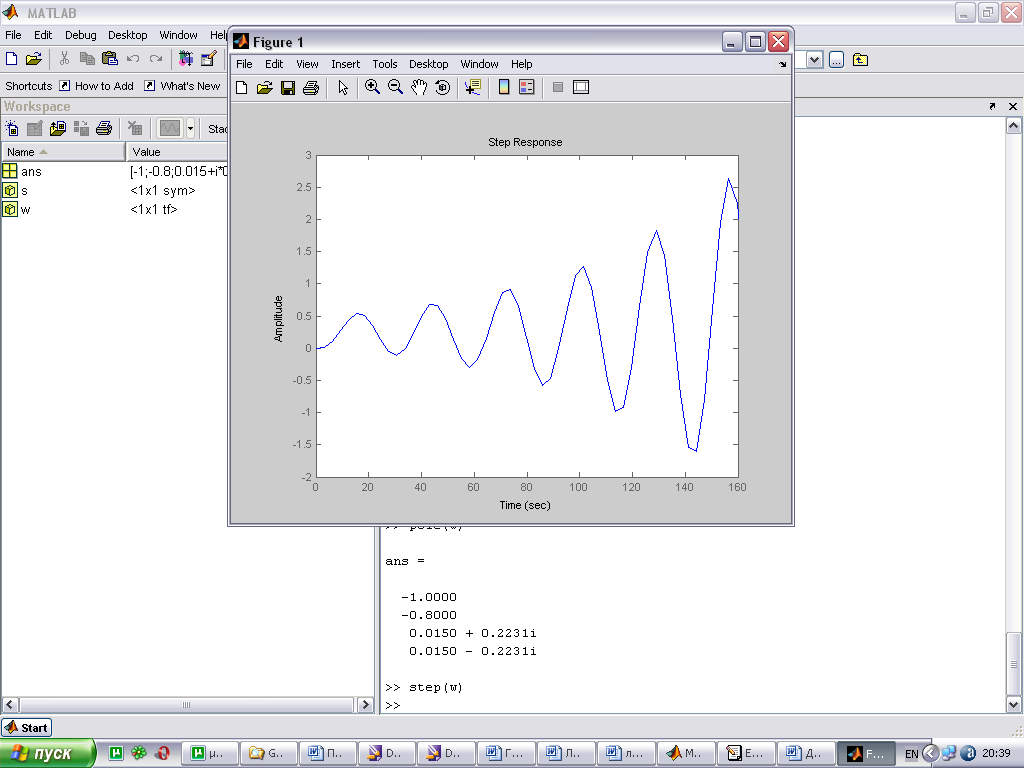
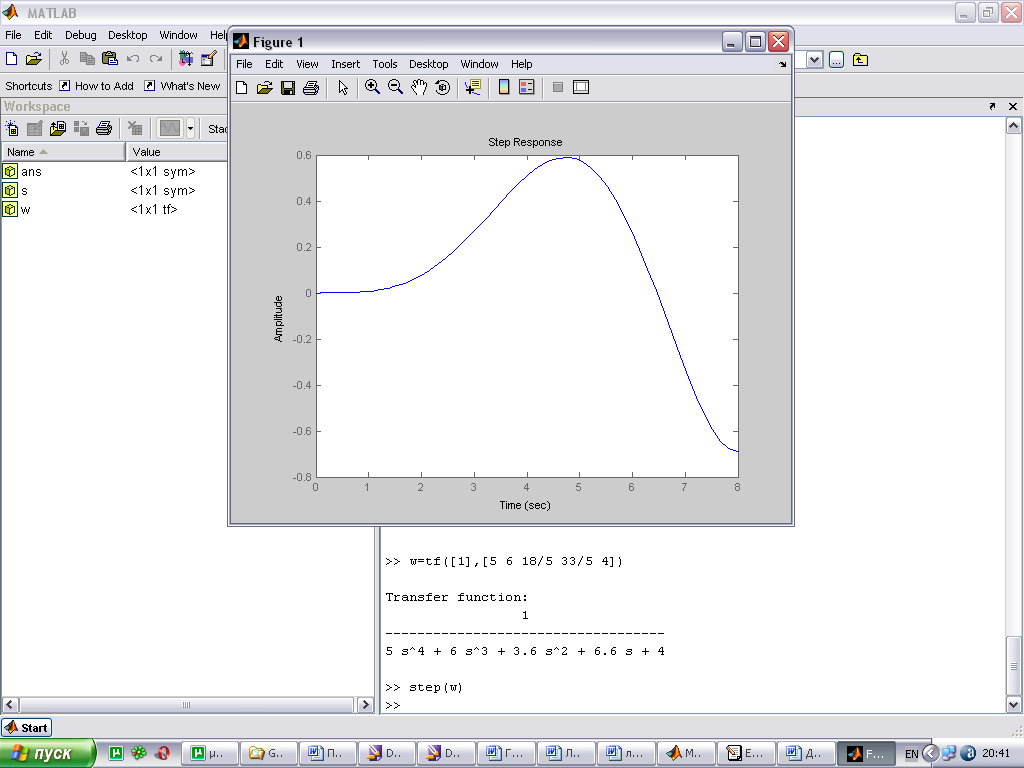
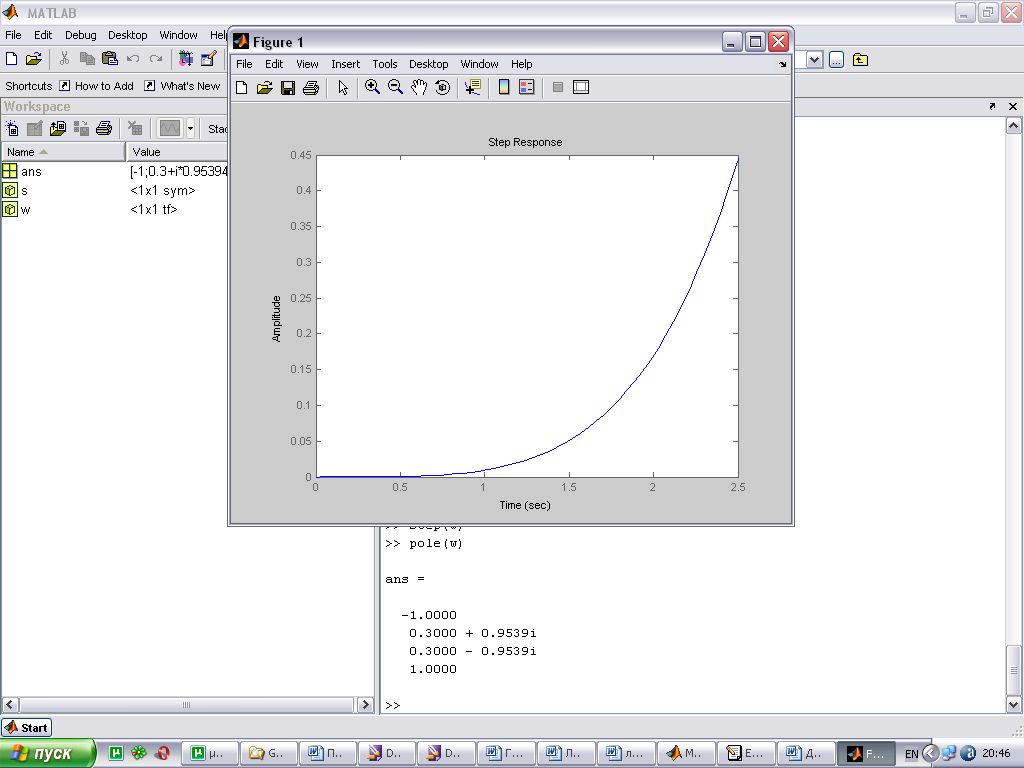
Если реакция системы на входное воздействие имеет установившийся характер (график сходящийся), то можно делать вывод о том, что система устойчива. Для оценки качества устойчивой системы полезно определить ряд показателей, которые кратко описывают некоторые характерные свойства динамики системы. Основные показатели качества системы:
hуст - установившееся значение – конечное значение переходной характеристики;
tн - время нарастания – время до момента, когда переходная характеристика впервые достигает значения hуст;
перерегулирование -
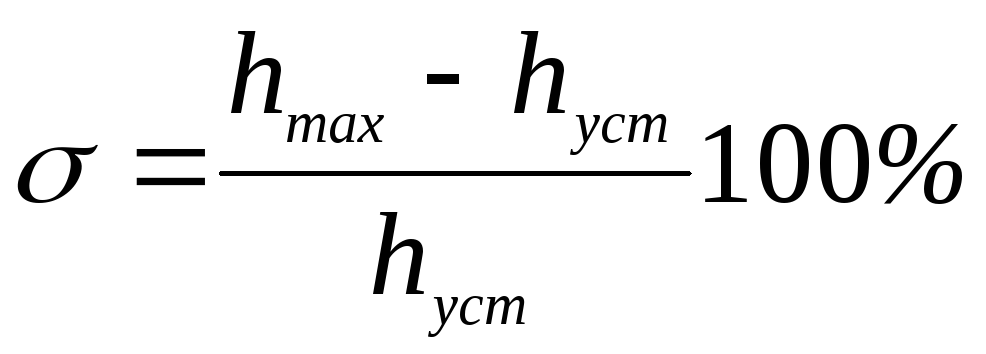;время регулирования tр – время, за которое переходный процесс заканчивается (с заданной точностью
).
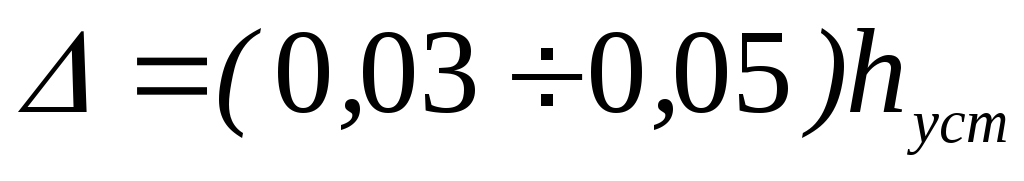;число колебаний n – число колебаний переходной характеристики за время tр. Первый выброс не учитывается;
частота колебаний -
.
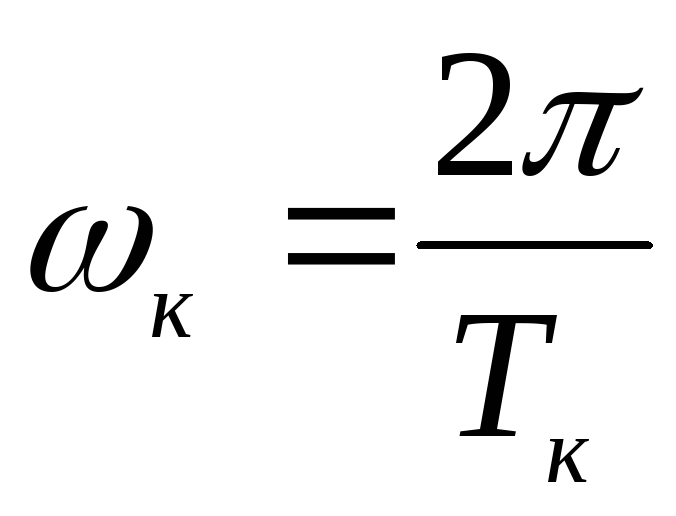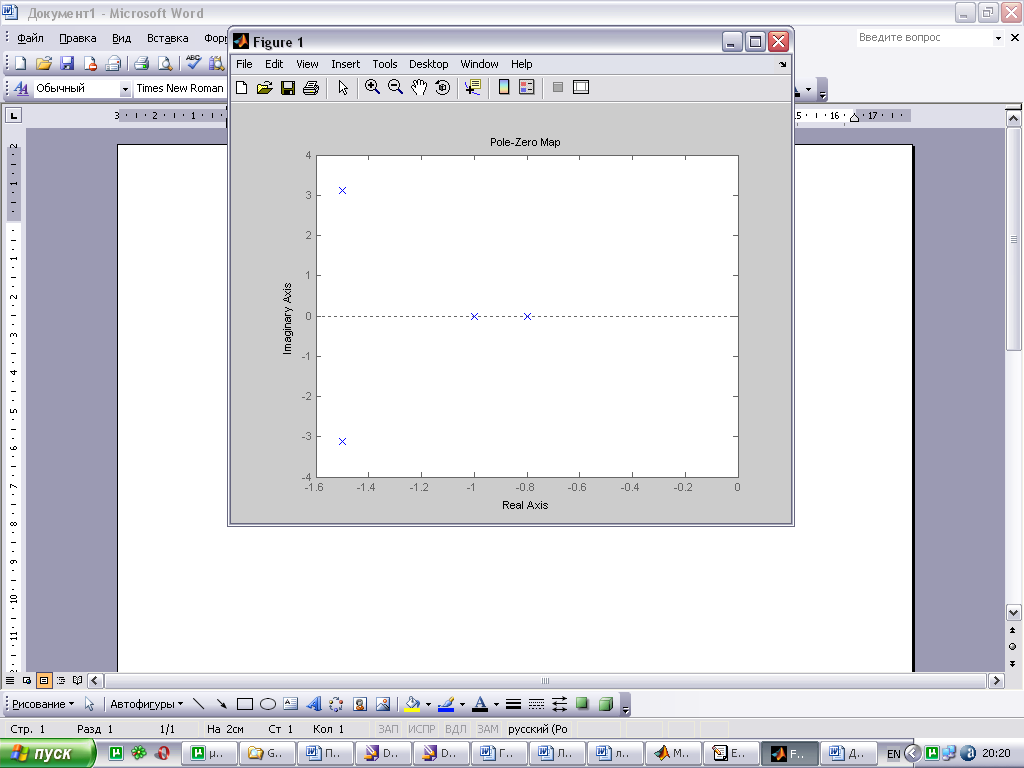
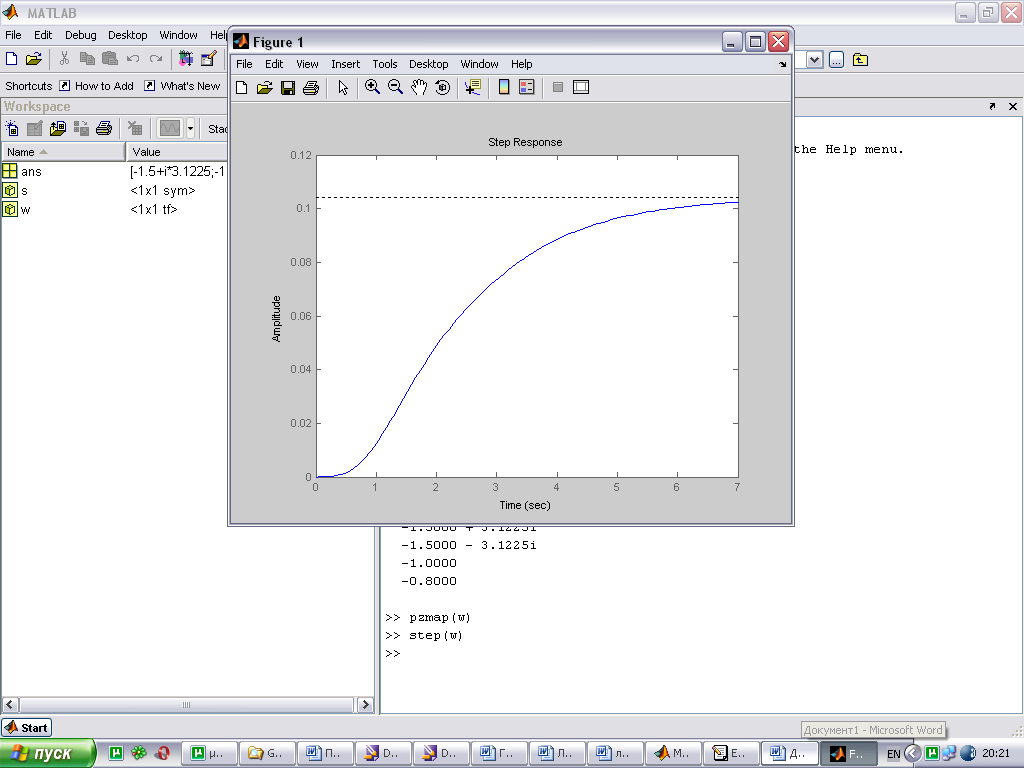
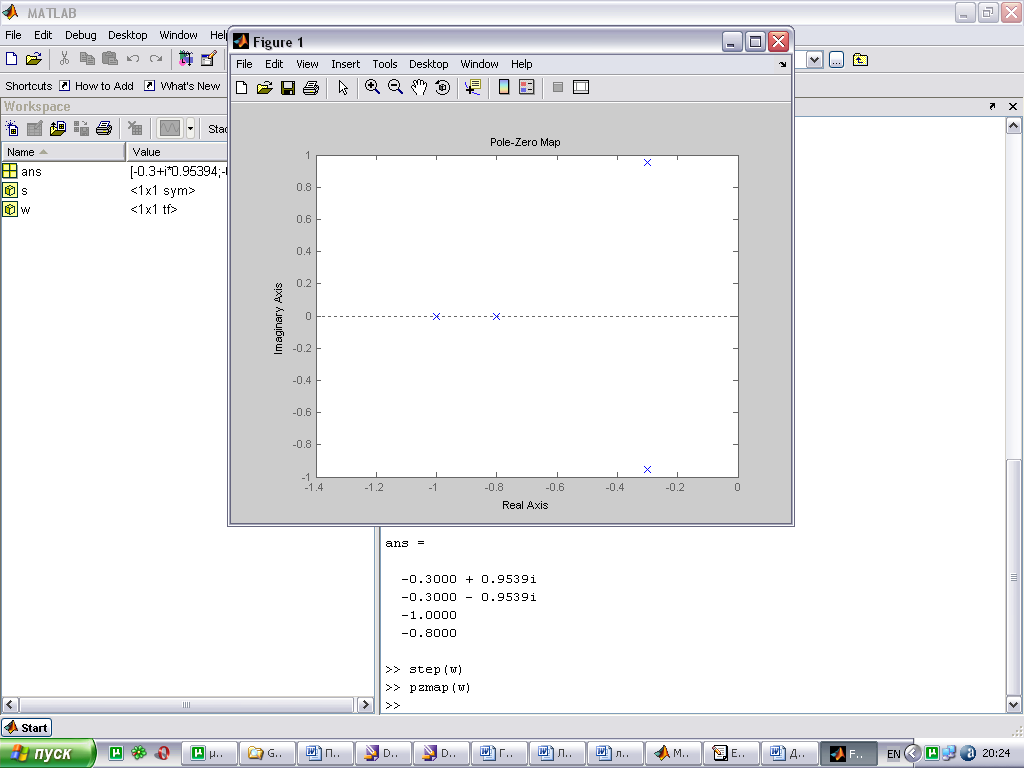
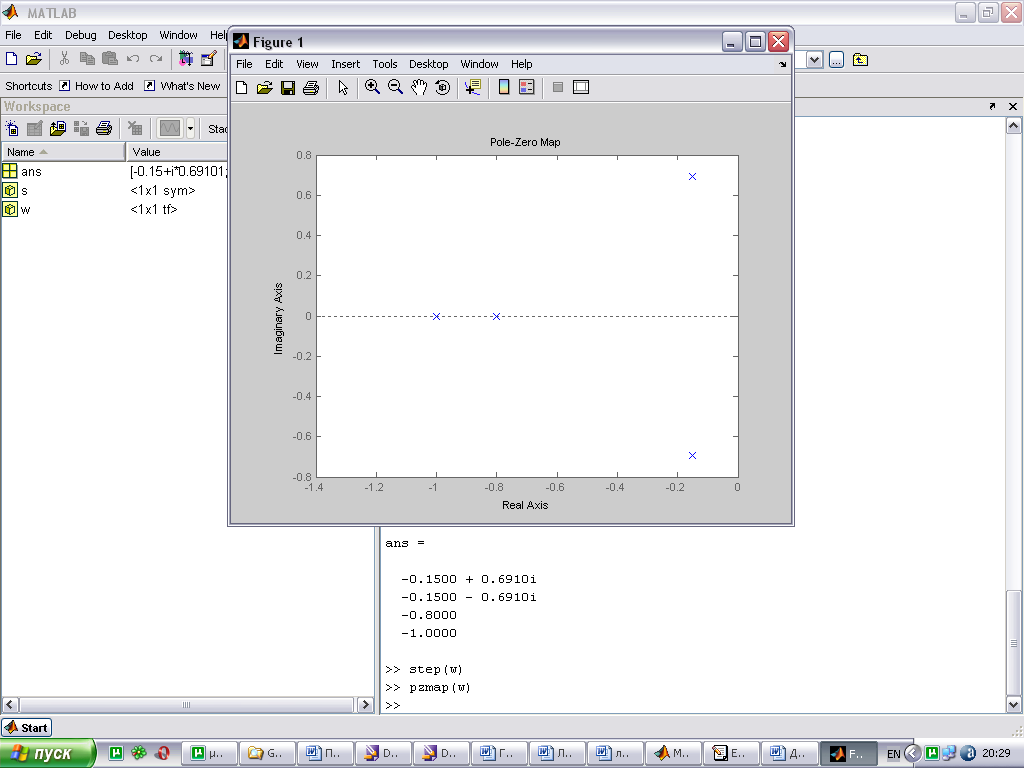
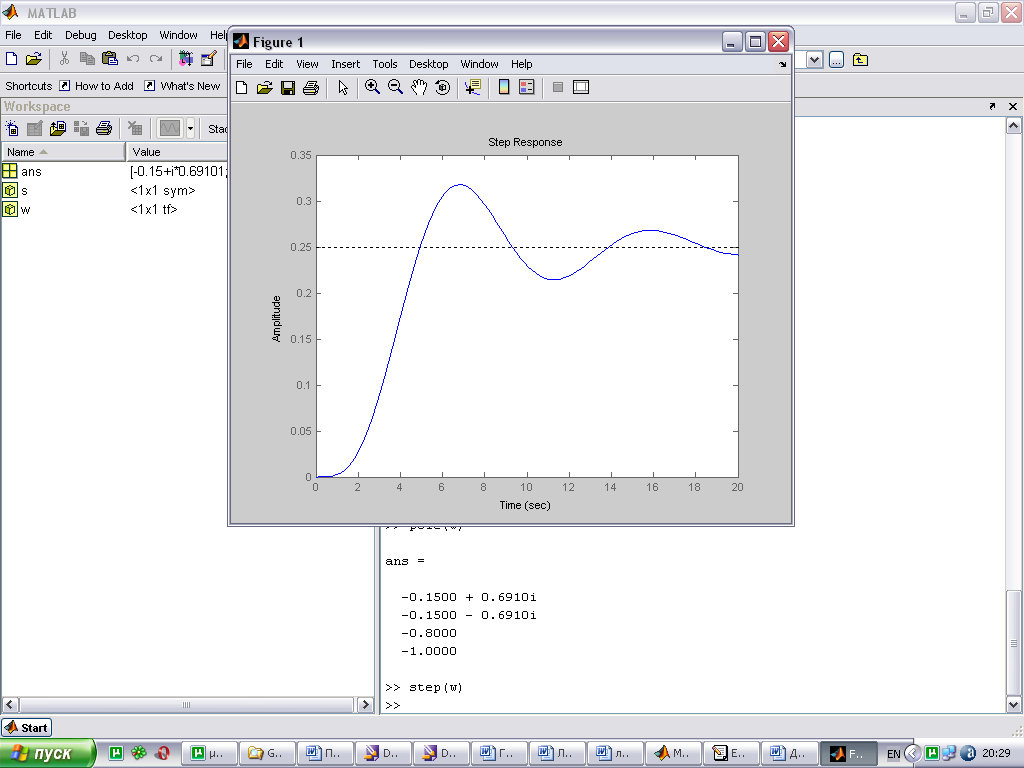
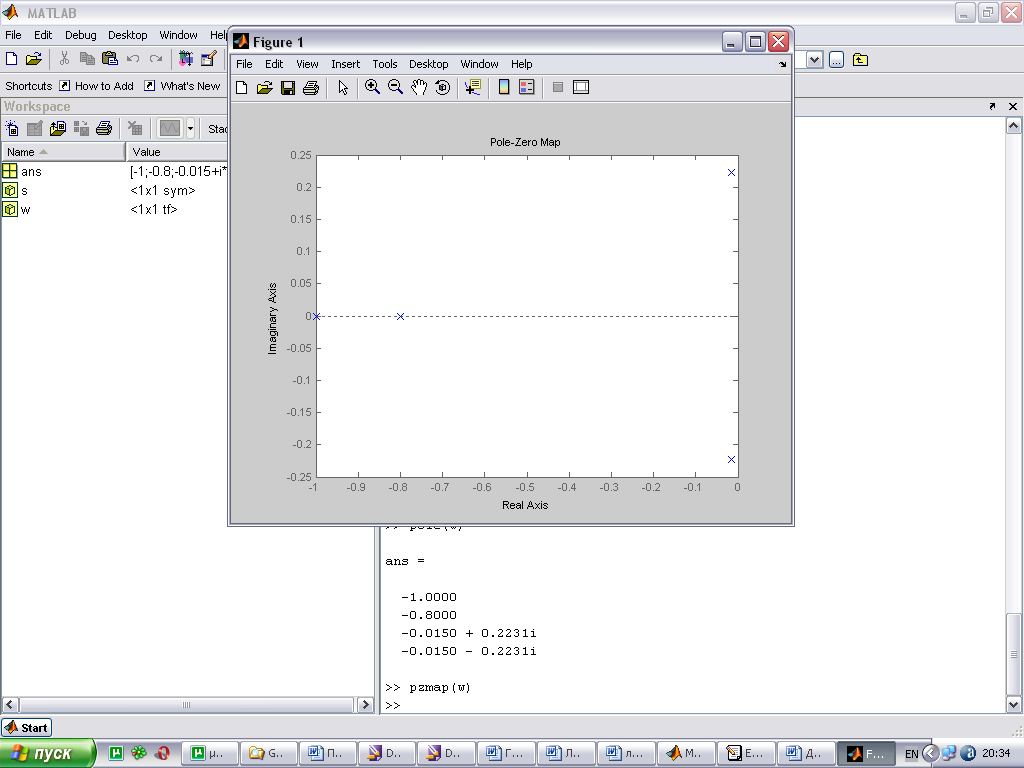
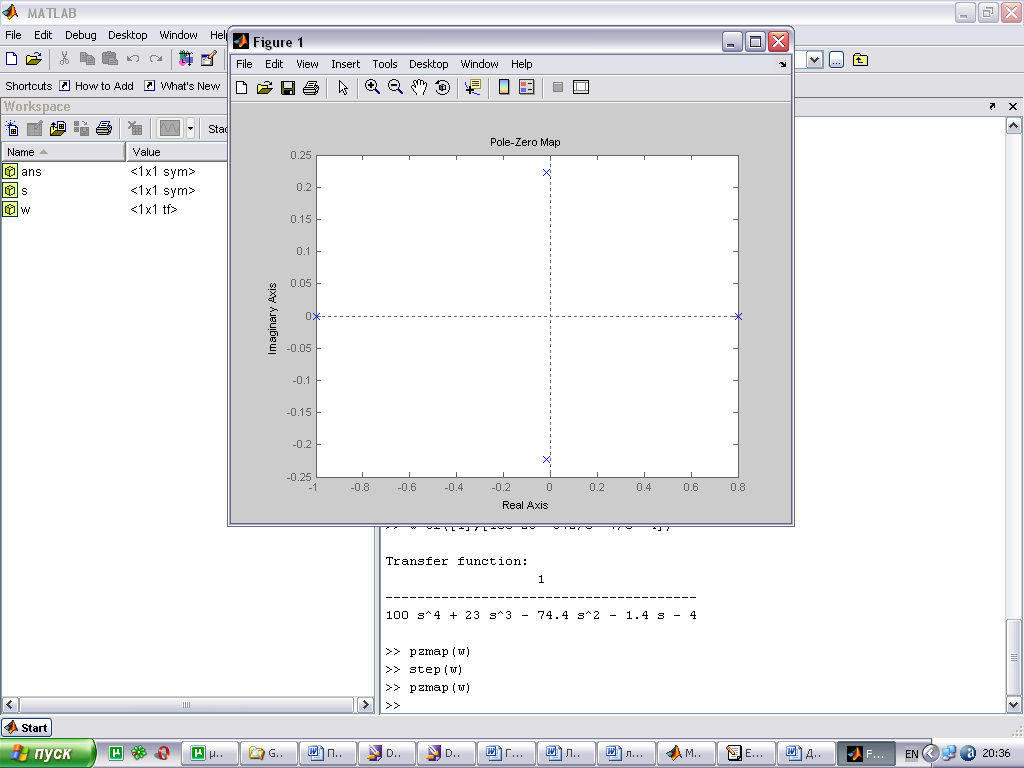
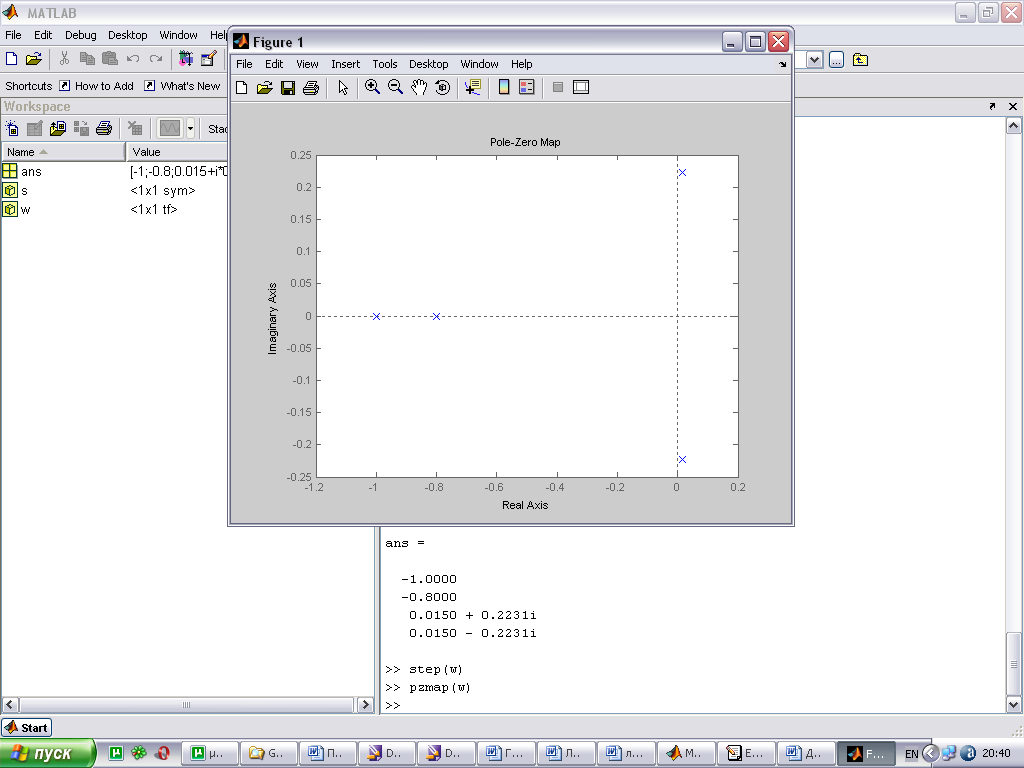
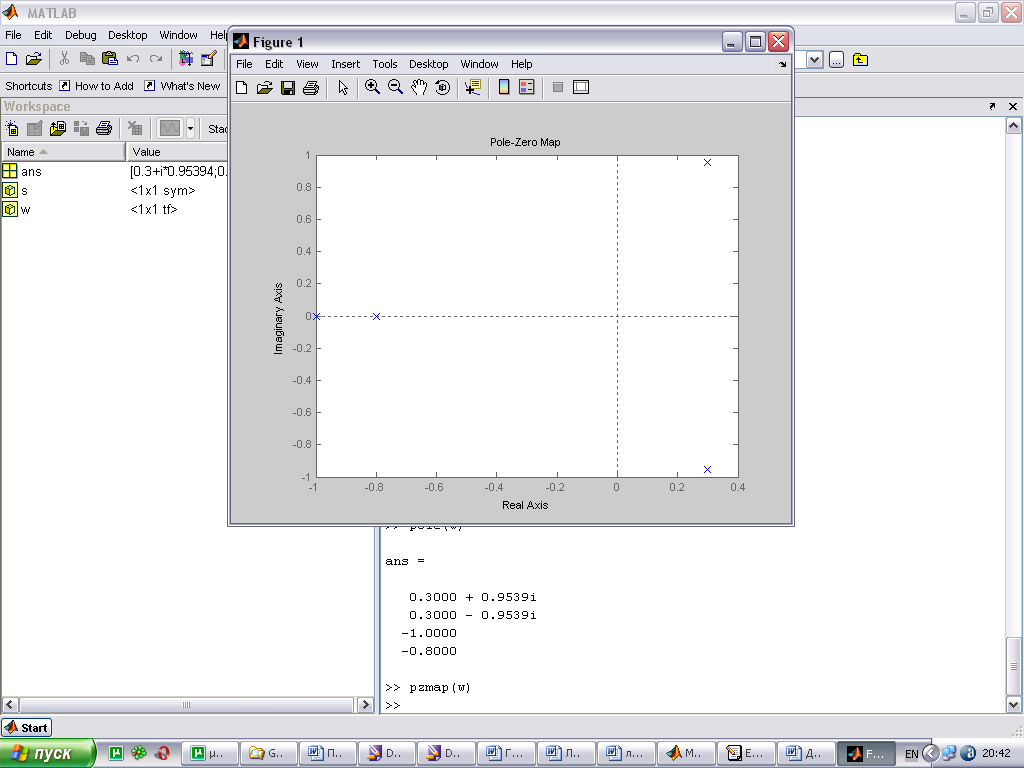
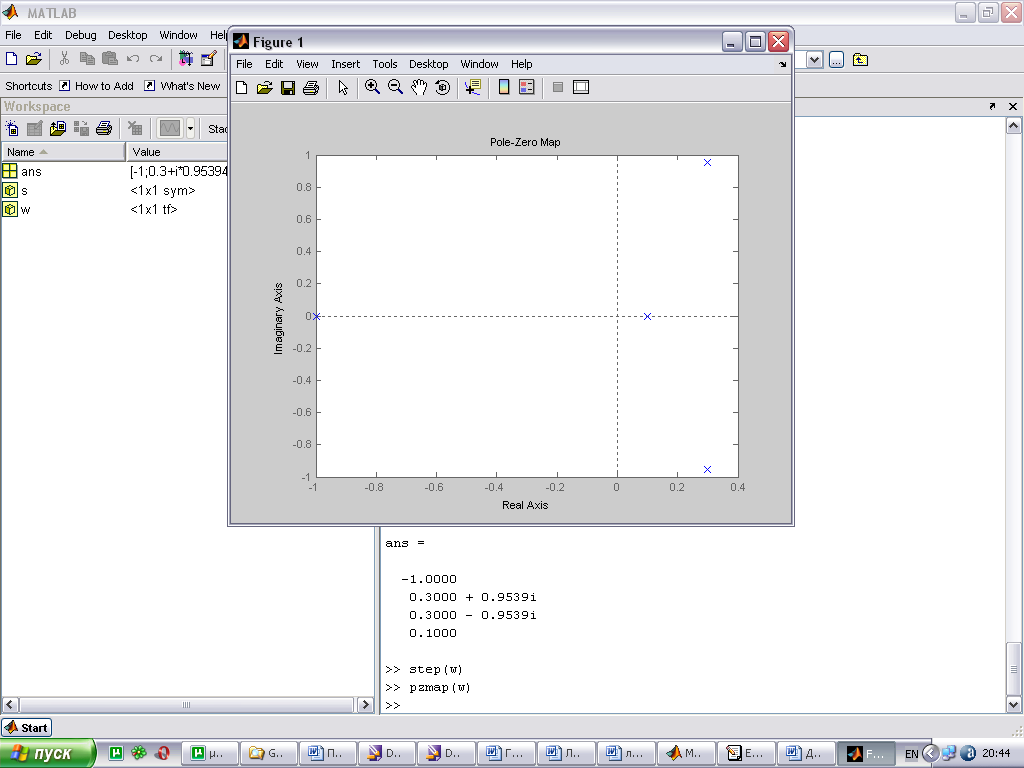
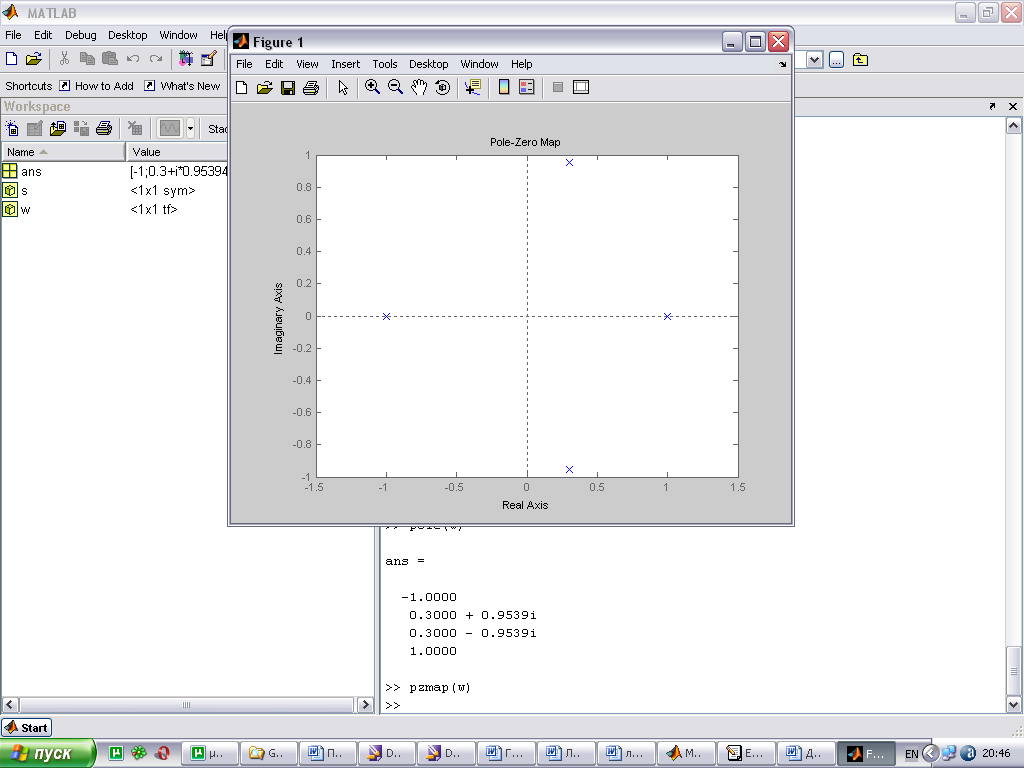
Связь расположения корней на комплексной плоскости и вида переходной характеристики.
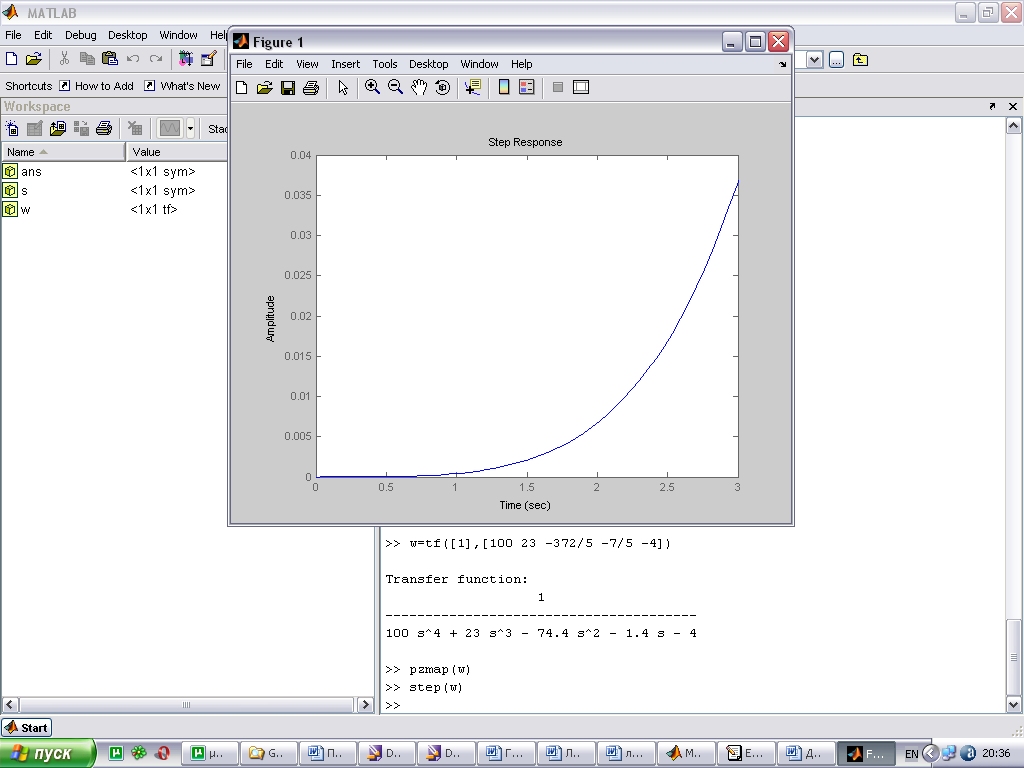
По расположению корней характеристического уравнения системы на комплексной плоскости можно судить о виде переходной характеристики. Если все корни уравнения лежат слева от мнимой оси (а это свидетельствует об устойчивости системы), то переходная характеристика будет иметь установившийся характер, т.е. будет сходится к конечному значению; иначе переходная характеристики будет иметь расходящийся вид, амплитуда будет стремиться к бесконечности.
При этом на вид переходной характеристики влияет так же и вид корней: реальные или комплексные. Если среди корней характеристического уравнения будут комплексно сопряженная пара корней, то переходная характеристика будет иметь колебательный вид; если все корни будут вещественными, то переходная характеристика будет монотонной.
|
расположение корней |
переходная характеристика |
|
степень колебательности = 2,08
|
|
|
степень колебательности = 3,18
|
|
|
степень колебательности = 4,6
|
|
|
степень колебательности = 14,87
|
|
|
степень колебательности = 14,87
|
|
|
степень колебательности = 14,87
|
|
|
степень колебательности = 3,18
|
|
|
степень колебательности = 3,18
|
|
|
степень колебательности = 3,18
|
|
Задание №3*:
Дано: дифференциальное уравнение системы
,
предполагается a2= 1, таблица с остальными коэффициентами дифференциального уравнения приведена ниже.
Требуется:
определить передаточную функцию W(s) системы;
найти переходную h(t) и импульсную переходнуюw(t) функции;
построить графики функций h(t) иw(t) на миллиметровке.
Варианты задания
|
Номер варианта |
Коэффициенты дифференциального уравнения | |||
|
a1 |
a0 |
b1 |
b0 | |
|
1 |
7 |
10 |
0 |
10 |
|
2 |
10 |
25 |
10 |
25 |
|
3 |
11 |
28 |
0 |
28 |
|
4 |
11 |
28 |
14 |
28 |
|
5 |
8 |
12 |
0 |
12 |
|
6 |
14 |
49 |
12 |
49 |
|
7 |
9 |
18 |
0 |
18 |
|
8 |
8 |
12 |
8 |
12 |
|
9 |
15 |
50 |
0 |
50 |
|
10 |
6 |
9 |
9 |
9 |
|
11 |
6 |
5 |
0 |
5 |
|
12 |
15 |
50 |
20 |
50 |