1.2 Графические способы описания систем: структурные схемы, графы, статические характеристики. Переход от одной формы к другой.

В теории управления широко применяется несколько графических способов описания системы управления: структурная схема, граф системы, статическая характеристика.

Структурной схемойсистемы управления называют графическое представление ее математической модели в виде соединений звеньев с указанием входных и выходных сигналов. Основными элементами структурной схемы являются: звено, узел, сумматор и элемент сравнения.

а	б		в		г
д		е		ж

Рисунок – Элементы структурных схем

Графомназывается совокупность множества V точек, называемых вершинами, и множества R простых (т.е. самонепересекающихся) кривых, называемых ребрами.

Рисунок – Граф системы управления

Статическая характеристиказвена системы управления – зависимость выходного сигнала звена от входного сигнала в статическом режиме, представленная в графической форме.

Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим режимом.

Рисунок – Виды статических характеристик звеньев

1.3 Переход от одной математической формы описания к другой

Рассмотрим пример перехода от одной формы представления к другой.

Дифференциальное уравнение объекта имеет вид:

.

Необходимо описать рассматриваемый объект с помощью известных форм.

Запишем дифференциальное уравнение объекта в следующем виде:

.

Тогда, используя оператор дифференцирования , запишем уравнение объекта в операторном виде:

.

По формуле (1.7) передаточная функция в операторном виде для заданного объекта:

.

Заменив оператор дифференцирования на оператор Лапласазапишем передаточную функцию объекта в изображения Лапласа:

.

Задание №1.1

для объекта, заданного одной из форм описания линейной динамической системы, привести другие формы описания (за исключением формы пространства состояний).

№	математическое описание объекта	№	математическое описание объекта
1		2
3		4
5		6
7		8
9		10
11		12

В теории управления пространство состояний - один из основных методов описания поведения динамической системы.

Иногда возникает необходимость прямого и обратного перехода от записи системы в виде передаточной функции к форме описания с помощью пространства состояний. Прямой переход в такой задаче неоднозначен, т.е. существует бесконечное множество троек матриц, в то время как обратный переход однозначен. Существует три стандартных схемы перехода от передаточной функции к пространству состояний: последовательная схема, параллельная и нормальная.

Рассмотрим методику перехода по каждой схеме.

Последовательная схема

Задано дифференциальное уравнение, описывающее состояние системы:

.

Тогда передаточная функция для такой системы будет иметь вид:

.

Приведем передаточную функцию системы к виду последовательно соединенных звеньев первого порядка, т.е.

.

Структурная схема для такого вида передаточной функции имеет вид:

Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

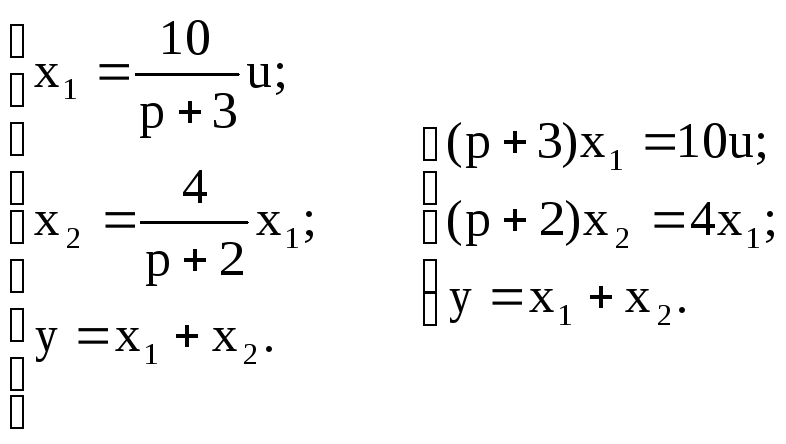
Учитывая, что p– это оператор дифференцирования, т.е., запишем

Тогда, принимая во внимание, что типовая форма записи метода пространства состояний имеет вид:

запишем матрицы A,BиC:

На основании полученных уравнений получим структурную схему для физической системы.

Структурная схема физической системы это структурная схема специфической конфигурации, состоящая из интеграторов, коэффициентов усиления и сумматоров. Данная структурная схема представляет собой заготовку для исследования системы с использованием компьютера.

Параллельная схема

Передаточная функция системы имеет вид:

.

Приведем передаточную функцию системы к виду параллельно соединенных звеньев первого порядка, т.е.:

Тогда запишем следующее:

Структурная схема для такого вида передаточной функции имеет вид:

Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

Учитывая, что p– это оператор дифференцирования, т.е., запишем:

Запишем матрицы A,BиC:

На основании полученных уравнений получим структурную схему для физической системы.

Нормальная схема

Передаточная функция системы имеет вид:

Структурная схема для такого вида передаточной функции имеет вид:

Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

Учитывая, что p– это оператор дифференцирования, т.е., запишем:

Учитывая то, что при использовании метода пространства состояний матричная форма записи системы дифференциальных уравнений составляется относительно ДУ первого порядка, понизим уравнение второго порядка относительно сигнала , введя промежуточный сигналтак, что

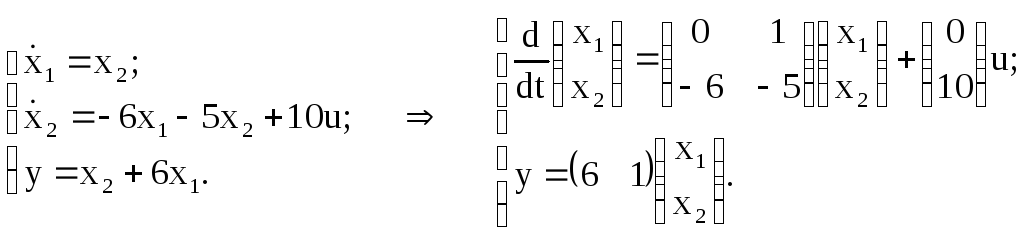
Запишем матрицы A,BиC:

На основании полученных уравнений получим структурную схему для физической системы.

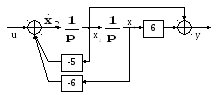
Таким образом, используя три основных схемы перехода можно перейти от формы представления системы в виде передаточной функции к форме пространства состояний.

Как уже было отмечено, существует и обратный путь перехода, т.е. от формы описания с помощью пространства состояния к операторной передаточной функции.

здесь - единичная матрица.

Тогда относительно выходного сигнала можно записать:

,

а выражение для передаточной функции имеет вид:

,

здесь - обратная матрица для матрицы^*.

Таким образом, зная матрицы A,BиC, можно найти выражение для операторной передаточной функции.