
- •«Тюменский государственный нефтегазовый университет» Институт промышленных технологий и инжиниринга
- •Электрические аппараты
- •Аннотация
- •Содержание
- •Введение
- •Критерии оценки работы студента
- •Общие требования к выполнению и оформлению работ
- •2. Электродинамические усилия в электрических аппаратах
- •Отключение электрических цепей
- •3.1. Исполнительный механизм с вращательным движением
- •3.2. Исполнительный механизм с поступательным движением
- •3.3. Передаточное устройство с кривошипно-шатунной передачей
- •3.4. Примеры расчетов сил и моментов сопротивления для некоторых типов механизмов
- •Электромагниты
- •Контроллеры, командоаппараты и реостаты
- •Электромагнитные и тепловые реле
- •Варианты индивидуального задания
- •Список рекомендуемой литературы:
- •Электрические аппараты
Контроллеры, командоаппараты и реостаты
Задачи
на определение времени решаются
интегрированием уравнения движения
(1) после разделения переменных. Для
![]() (что характерно для многих производственных
установок, в которых
(что характерно для многих производственных
установок, в которых![]() и система управления обеспечивает
постоянное среднее значение пусковых
и система управления обеспечивает
постоянное среднее значение пусковых![]() и тормозных
и тормозных![]() моментов), а также при
моментов), а также при![]() ,
в результате интегрирования уравнения
(2), получим следующие расчетные формулы
для вычисления времени пуска
,
в результате интегрирования уравнения
(2), получим следующие расчетные формулы
для вычисления времени пуска![]() и торможения
и торможения![]() электропривода, с,
электропривода, с,
![]() ;
(22)
;
(22)
![]() .
(23)
.
(23)
Так как путь, проходимый приводом при неустановившемся движении,
![]() ,
(24)
,
(24)
то,
используя уравнения (22) и (23), получим
следующие выражения для определения
пути электропривода за период пуска
![]() п
и торможения
п
и торможения
![]() т:
т:
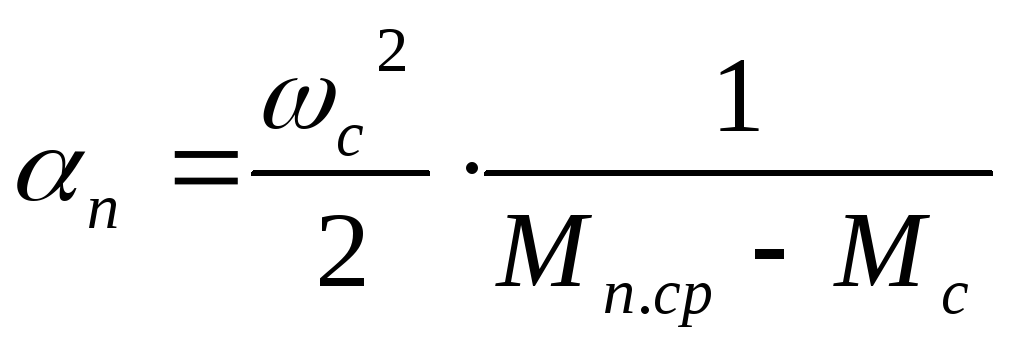 ;
(25)
;
(25)
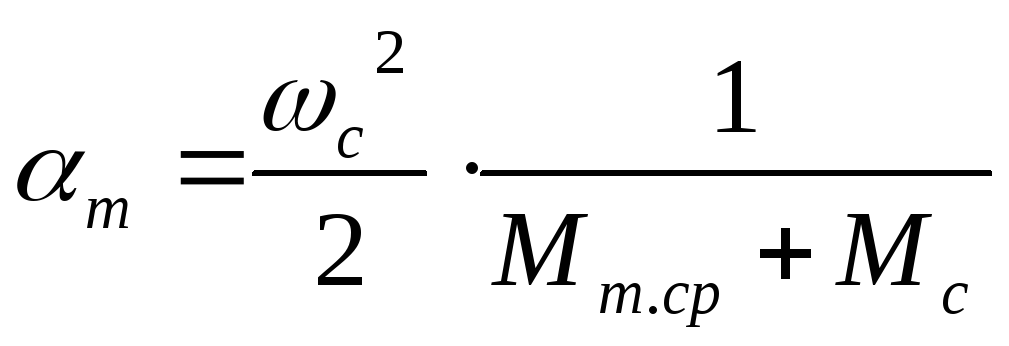 .
(26)
.
(26)
Для
конкретных кинематических систем
угловой путь двигателя пересчитывается
в угловое
![]() или линейное
или линейное![]() перемещение ИМ.
перемещение ИМ.
Пример
4. Определить
время пуска подъемника при опускании
груза в двух случаях: а) двигатель
развивает движущий момент
![]() = 160 Н·м;
б) двигатель развивает тот же по
величине тормозной момент.
= 160 Н·м;
б) двигатель развивает тот же по
величине тормозной момент.
Статический
момент на валу двигателя активный и
равен 320 Н·м. Момент инерции привода и
подъемника, приведенный к валу двигателя,
![]() =15
Дж∙с2.
Установившаяся скорость двигателя
=15
Дж∙с2.
Установившаяся скорость двигателя
![]() об/мин (
об/мин (![]()
![]() 8,7
с-1)
.
8,7
с-1)
.
Решение:
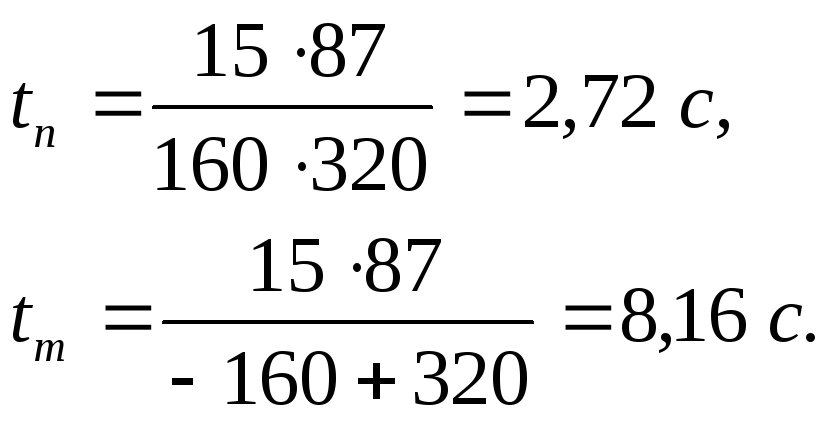
Пример
5. Тележка
разгоняется электроприводом до
номинальной скорости
![]() м/с
при постоянном статическом моменте
сопротивления. Момент инерции механизма,
приведенный к валу двигателя,
м/с
при постоянном статическом моменте
сопротивления. Момент инерции механизма,
приведенный к валу двигателя,![]() =
0,6 Н·м∙с2,
момент инерции двигателя
=
0,6 Н·м∙с2,
момент инерции двигателя
![]() = 0,15 Н·м∙с2,
номинальная скорость двигателя
= 0,15 Н·м∙с2,
номинальная скорость двигателя
![]() =1430
об/мин., динамический момент при разгоне
тележки
=1430
об/мин., динамический момент при разгоне
тележки![]() = 100 Дж =
= 100 Дж =![]() .
Определить время разгона тележки, путь
тележки и двигателя за период разгона
и их ускорения.
.
Определить время разгона тележки, путь
тележки и двигателя за период разгона
и их ускорения.
Решение. Время пуска тележки в соответствии с выражением (22)
![]()
Путь,
пройденный тележкой за период разгона
до скорости
![]() = 1,5 м/с,
= 1,5 м/с,
![]() ,
,
а ускорение при пуске тележки
![]()
Соответственно, угловой путь двигателя
![]()
Этот же результат получается, если вычислить
![]()
Угловое ускорение двигателя
![]()
Электромагнитные и тепловые реле
Из
выражения (23) для определения времени
торможения привода следует, что при
торможении вхолостую
![]() время снижения скорости определяется
величиной запасенной кинетической
энергии, пропорциональной моменту
инерции j,
и механическими потерями в приводе,
т.е.
время снижения скорости определяется
величиной запасенной кинетической
энергии, пропорциональной моменту
инерции j,
и механическими потерями в приводе,
т.е.
![]() (27)
(27)
Зная величину небольшого снижения скорости за краткий отрезок времени, когда переходный процесс w = f(t) можно считать линейным, на основании выражения (27)
![]() .
(28)
.
(28)
Пример 6. Определить момент инерции двигателя, если его скорость за 4 с после отключения от сети снижается на 300 об/мин. При работе двигателя вхолостую со скоростью 1400 об/мин он потребляет из сети мощность 3,6 кВт, половина которой по опытным данным расходуется на преодоление механических потерь.
Решение. Величина момента механических потерь
![]()
Момент инерции двигателя при указанном темпе снижения скорости на основании выражения (28):
![]()
Более точно величину момента инерции двигателя или электропривода вместе с ИМ можно определить по экспериментальным данным, полученным при опыте выбега (самоторможения) и при изменении потерь холостого хода.
Пример 7. По опытным данным, приведенным в таблице 6.1 и 6.2, определить момент инерции электропривода в различных системах единиц и пересчитать его на маховой момент во внесистемных единицах.
Таблица 6.1
Опыт самоторможения (выбега)
|
Время от начала выбега, с |
0 |
2 |
4 |
8 |
126 |
16 |
20 |
25 |
32 |
38 |
45 |
53 |
|
Скорость двигателя, об/мин |
1430 |
1300 |
1184 |
1050 |
926 |
830 |
716 |
600 |
454 |
334 |
218 |
96 |
Таблица 6.2
Опыт холостого хода
-
Скорость двигателя, об/мин
1337
1 242
1050
860
668
267
334
Мощность механических потерь, Вт
170
150
120
90
60
35
20
Решение. На основании опытных данных строятся кривая выбега ω = f(t) и характеристика механических потерь Р = f(ω). по которым строится расчетная кривая P = f(t), показанная на рисунке 6.
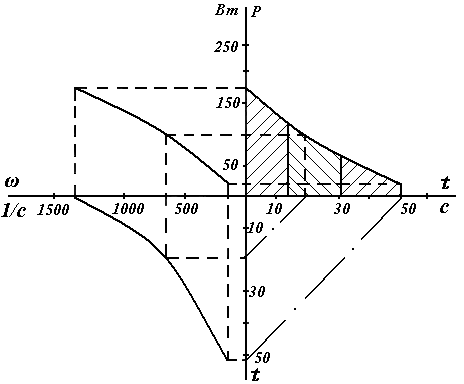
Рис. 6. Расчетная кривая выбега
Так
как в процессе выбега накопленная
кинетическая энергия
![]()
![]() расходуется на механические потери
(трение о воздух и в подшипниках привода),
то она может быть определена по площадиS
расчетной кривой P
= f(t),
построение
которой показано на рисунке 6.
расходуется на механические потери
(трение о воздух и в подшипниках привода),
то она может быть определена по площадиS
расчетной кривой P
= f(t),
построение
которой показано на рисунке 6.
То
есть S
=![]() ,
откуда определяется искомый момент
инерции привода. ПлощадьS
на кривой Р =
f(t)
определяется как сумма площадей трапеций
при изменении скорости в пределах от
ω1
= 170 с-1
(t
= 0, начало
расчета по кривой выбега) до ω2
= 25с-1
(t
= 52). Ведя расчет таким образом, находим
,
откуда определяется искомый момент
инерции привода. ПлощадьS
на кривой Р =
f(t)
определяется как сумма площадей трапеций
при изменении скорости в пределах от
ω1
= 170 с-1
(t
= 0, начало
расчета по кривой выбега) до ω2
= 25с-1
(t
= 52). Ведя расчет таким образом, находим
S
=
![]() =
=![]() =J
.14137,5
Дж∙c2.
=J
.14137,5
Дж∙c2.
Подставляем в полученное выражение значение S = 4657,5 м2:
4657,5 = J .14137,5.
Отсюда получаем значение J:
J = 0,329 Дж . с2 (Н . м .с2).
Маховой момент привода GD2 = 4J = 4.0,329 = 1,316 кг. м2 .
В технической системе единиц
![]() кгс.
м
. c2.
кгс.
м
. c2.
В Рис.
7. Подъемная установка 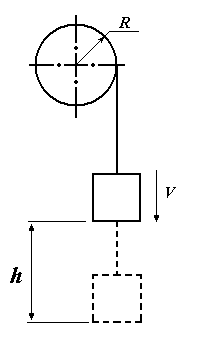
![]() , (29)
, (29)
где ускорение поступательного равноускоренного движения груза определяется по параметрам h и t из опыта:
![]() .
(30)
.
(30)
Момент сопротивления движению, создаваемый трением в подшипниках, определяется по минимальной массе то, при которой начинается движение шкива на опыте:
![]() .
(31)
.
(31)
Вращающий момент М, обеспечивающий ускоренное движение шкива и груза:
![]() .
(32)
.
(32)
Преобразуя уравнение (29) с помощью уравнений (30)…(32), получим следующее выражение для определения момента инерции, кг . м2:
 .
(33)
.
(33)
Пример 8. Определить момент инерции двигателя, который при поднятых щетках раскручивается грузом массой т = 1,2 кг, подвешенным на шкиве радиусом R = 0,08 м. За 4 с груз успевает опуститься на высоту h = 7,2 м. Масса груза, при которой преодолевается момент сопротивления в подшипниках, то = 0,1 кг.
Решение. Линейное ускорение при падении груза
![]() м/с2.
м/с2.
Момент инерции двигателя со шкивом в соответствии с уравнением (33)
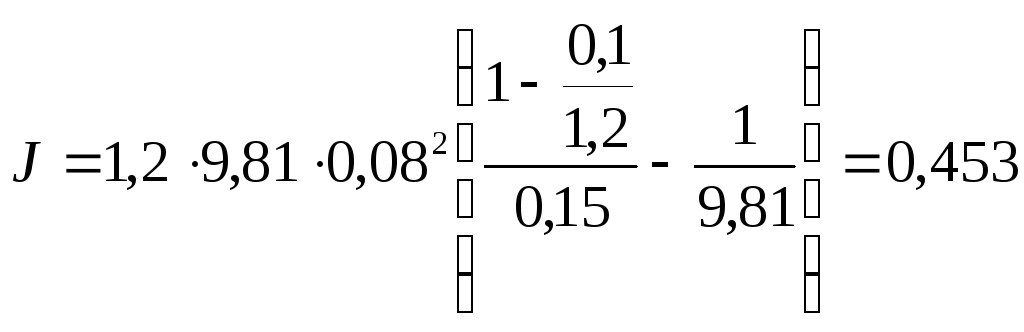 кг.м2.
кг.м2.
Если определять момент инерции приближенно, без учета потерь в подшипниках, то есть, принимая то = 0, получим:
![]() кг.м2.
кг.м2.
Для простых геометрических тел вращения, состоящих из однородных материалов, для определения момента инерции (J = mp2, где p - радиус инерции) можно пользоваться формулами, приведенными в таблице 6.3.
Таблица 6.3
Формулы для расчета момента инерции тел вращения
-
Сплошной цилиндр
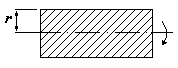
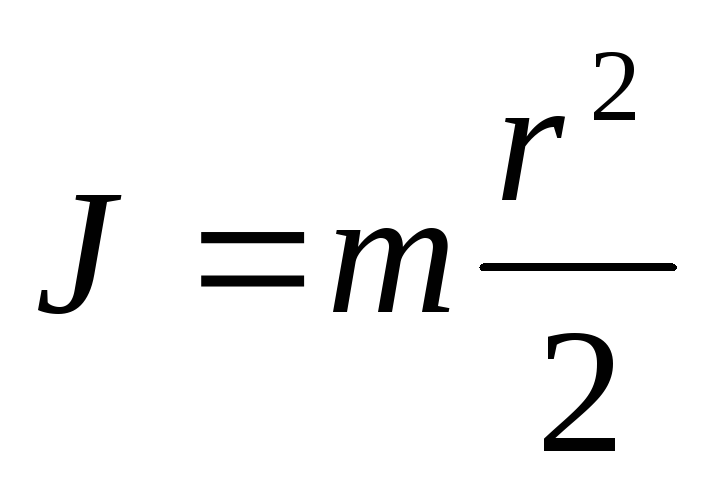
Полый цилиндр
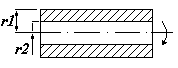
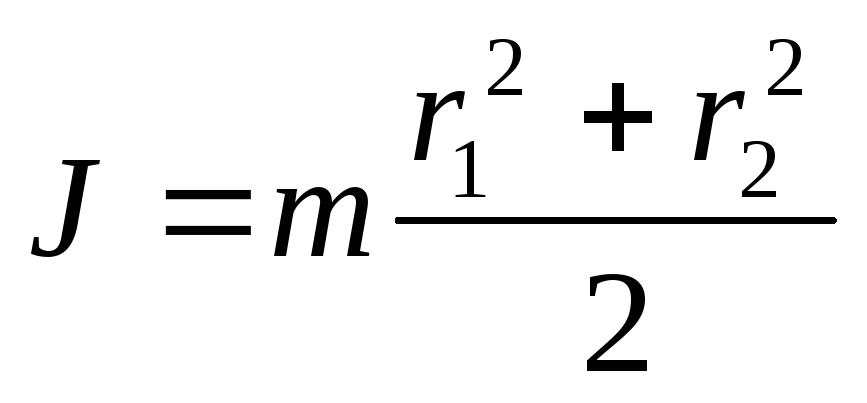
Сплошной конус
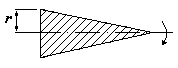
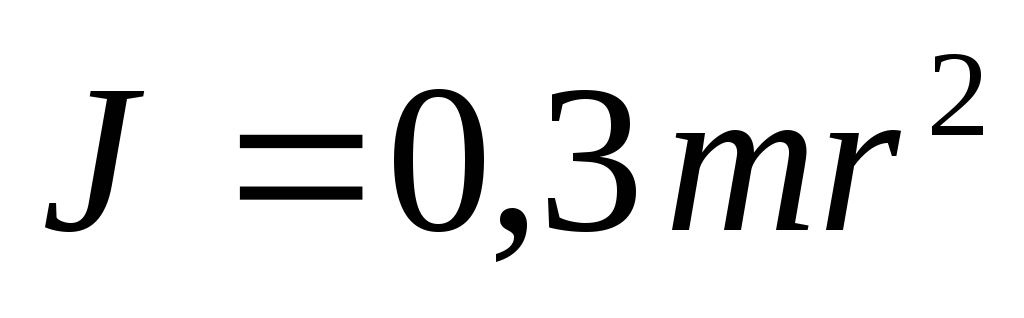
Пример 9. Определить, во сколько раз изменится момент инерции якоря двигателя при увеличении его диаметра в 1,5 раза при неизменной длине, а также при таком же увеличении длины якоря и неизменном диаметре его. Якорь двигателя принять за сплошное однородное тело.
Решение. В соответствии с формулами таблице 3,
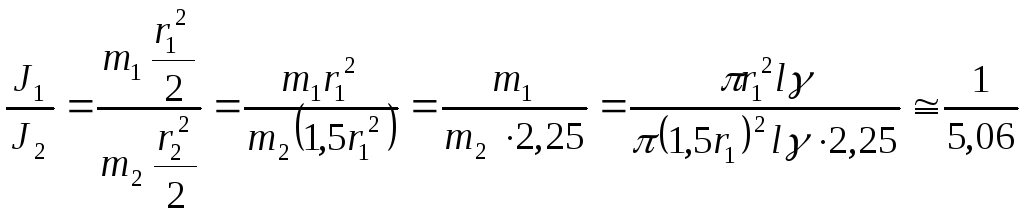 .
.
Таким образом, при заданных условиях увеличение радиуса якоря в 1,5 раза ведет к увеличению его момента инерции примерно в 5 раз. Аналогичные расчеты показывают, что увеличение длины якоря в 1,5 раза при неизменном диаметре во столько же увеличивается и его момент инерции.
