1. Постановка экспериментальной задачи
1.1. Металл как потенциальная яма
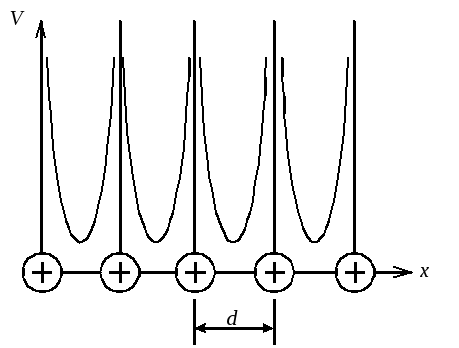
Электроны проводимости в металле совершают хаотическое тепловое движение, но вылететь за поверхность металла могут лишь наиболее быстрые электроны, обладающие достаточной кинетической энергией. Это объясняется тем, что металл для электронов представляет “потенциальную яму”, которую они не могут свободно покинуть. Для выхода из нее электронам требуется преодолеть некоторый потенциальный “барьер”. Наличие этого “барьера” объясняется следующим образом. Положительные ионы, образующие решетку металла, создают внутри металла электрическое поле с положительным потенциалом, периодически меняющимся при перемещении вдоль прямой, проходящие через узлы решетки (рис.1). В грубом приближении этим изменением можно пренебречь и считать потенциал во всех точках металла одинаковым и равным V0 (рис.2а). Свободный электрон, находящийся в таком поле, обладает отрицательной потенциальной энергией Ep = - q V0, где q - заряд электрона.
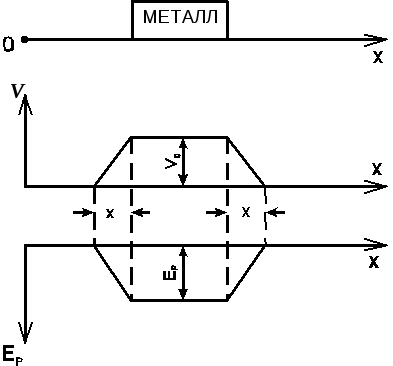
На рис.2б показано изменение потенциальной энергии электрона при работе из вакуума в металл: в вакууме Ep = 0, в металле Ep = -q V0. Это изменение хотя и носит характер скачка, но происходит не мгновенно, а на протяжении отрезка Х. Из рис.2 видно, что металл является для электрона потенциальной “ямой”.
Выход
электрона из металла, как из потенциальной
“ямы”, требует затраты работы по
преодолению сил, удерживающих его в
металле. Эту работу называют работой
выхода электронов. Так как изменение
потенциальной энергии электронов при
выходе из металла происходит лишь на
отрезке Х непосредственно у поверхности
металла, то и действие сил препятствующих
выходу, сосредоточенно только на этом
отрезке. Внутри металла и вне этого
отрезка потенциальная энергия электрона
постоянна, и эти силы равны нулю. (Т.к.
и если Ep =
const, то dEp =
0 и E = 0)
|
|
|
|
Рис.1 Изменение потенциала в металле вдоль линейной цепочки положительных ионов |
Рис.2. Металл как потенциальная яма для электрона (V – потенциал; EP –потенциальная энергия) |
1.2. Распределение свободных электронов в металле по энергиям
Состояние свободных электронов в металле описывается квантовой статистикой Ферми-Дирака, согласно которой распределение электронов по энергиям имеет вид:
(1)
где dn/n - относительное число свободных электронов с энергиями от E до (E + dE) в единице объема металла; - некоторая постоянная величина; Т - абсолютная температура; k - постоянная Больцмана; EF - уровень Ферми.
На рис.3 показано соответствующее формуле (1) распределение свободных электронов в металле по энергиям при абсолютном нуле (кривая I) и при некоторой температуре Т > 0 (кривая II).
При Т = 0 не существует электронов с энергиями, большими EF.
Заштрихованная площадь дает число состояний, заполненных электронами при абсолютном нуле. Нагревание металла сопровождается переходом электронов с уровней, примыкающих к уровню Ферми, на уровни, лежащие выше EF. В результате кривая распространения электронов по энергиям примет вид T > 0 в этой же области вид, показанный пунктирной линией. Площадь под этой кривой считается той же, какой она была при абсолютном нуле (т.е. общее число электронов не изменится).
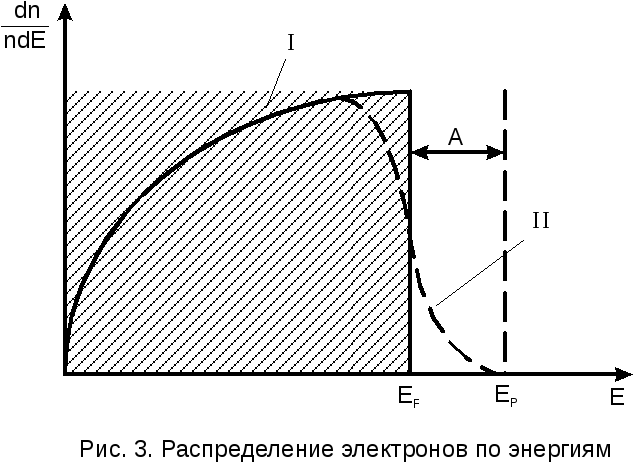
Кривая II показывает, что при повышении температуры характер разделения электронов по энергиям изменится незначительно.