1.2. Контактная разность потенциалов и барьерная ёмкость электронно-дырочного перехода в полупроводниках

Рассмотрим случай, когда p-n-переход создан в кристалле полупроводника введением в одну его область акцепторных, а в другую – донорных примесей. Энергетические диаграммы отдельныхp- иn- областей показаны на рис.2а. В р-области уровень Ферми расположен вблизи потока валентной зоны, а вn-области – вблизи дна зоны проводимости. Если р- иn- области контактируют, на границе раздела возникают большие градиенты концентрации примеси. Под действием градиентов концентрации начнётся диффузия дырок из р-области вn-область и встречная диффузия электронов. В областиp-n-перехода встречно движущиеся электроны и дырки рекомбинируют.

После ухода основных носителей заряда в приграничных областях полупроводника остаются электрически нескомпенсированные ионы примесей: отрицательно заряженные акцепторы в дырочном полупроводнике и положительно заряженные доноры в электронном. Таким образом, вблизи границы раздела возникают области объёмного заряда. Эти нескомпенсированные заряды создают электрическое поле, которое препятствует дальнейшему переходу носителей (электронов и дырок). Разность потенциалов между p- иn-областями в условиях равновесия и будет контактной.

Энергетическая диаграмма p-n-перехода представлена на рис.2б. Уровни Фермиn- и р-областях устанавливается на одинаковой глубине, т.е. горизонтально, а созданное объёмным зарядом поле приводит к изгибу зон. Вдали от контакта взаимное расположение зоны проводимости, валентной зоны и уровней Ферми не изменяется. Контактная разность потенциалов пропорциональна изгибу зон.

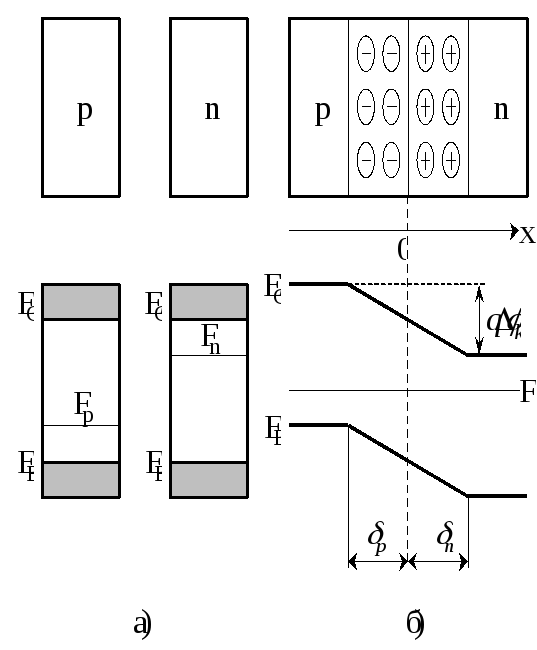
Рис.2. Энергетические диаграммы полупроводников:

а – областей p- и n-типа электропроводности;

б – p-n-перехода.

Область объёмного заряда представляет собой двойной слой противоположных по знаку неподвижных зарядов. Этот двойной слой можно уподобить обкладкам плоского конденсатора, к которому приложена контактная разность потенциалов.

Электроёмкость такого конденсатора получила название барьерной, т.к. связана с существованием энергетического барьера между p- иn-областями. Значение барьерной электроёмкостиp-n-перехода можно вычислить по формуле для плоского конденсатора

, (3)

где - диэлектрическая проницаемость,

- электрическая постоянная,

- площадьp-n-перехода,

- ширина области объёмного заряда.

Изгиб энергетических зон, ширина области объёмного заряда, а, значит и барьерная ёмкость изменяются, если к p-n-переходу приложить внешнее напряжение. Принято считать внешнее напряжение положительным при прямом включении. В этом случае к р-области присоединён положительный полюс источника питания, а кn-области – отрицательный. При обратном включении напряжение считается отрицательным. Разность потенциалов междуp- иn- областями при обратном включенииp-n-перехода увеличивается до значения, ширина области объёмного заряда также увеличивается, а барьерная ёмкость уменьшается. В результате барьерная ёмкостьp-n-перехода зависит от контактной разности потенциалов и внешнего напряжения. Определим эту зависимость для наиболее простого случая, когда граница между электронной и дырочной проводимостями резкая и плоская. Проведём ось Х перпендикулярно границе, совместив с границей начало координат (см. рис.2б). Обозначим концентрацию акцепторов вp-области(считаем, что другие примеси вp-области отсутствуют), аналогично обозначим концентрацию доноров вn-области.

Запишем теорему Гаусса в дифференциальной форме:

, (4)

где - напряжённость электрического поля,

- объёмная плотность заряда.

В одномерном случае

, (5)

а формула (4) запишется в виде

(6)

Выражение (6) носит название Пуассона. Для областей иобъёмная плотность заряда равна нулю (полупроводник электрически нейтрален), поле вне области объёмного заряда отсутствует. В р-области приобъёмны заряд создаётся акцепторными примесями (концентрацией свободных носителей заряда можно пренебречь), аналогично дляn-области при

Решения уравнения Пуассона, наёденные отдельно для р- и n-области, «сшиваются» на границе (х=0) с помощью следующих граничных условий:

при , (7)

при , (8)

при , (9)

а также . (10)

В результате получим:

. (11)

Из (11) выразим ширину области объёмного заряда:

. (12)

В случае резко несимметричного перехода, когда одна из областей легирована более сильно, чем другая (или) формула (12) принимает вид:

. (14)

Отсюда следует, что зависимость линейна. Это условие лежит в основе метода определения контактной разности потенциалов. Измеряют значение барьерной ёмкости при различных обратных напряжениях, вычисляюти строят график зависимости. Точки при этом должны укладываться на прямую линию (в пределах погрешности измерений). Экстраполируя прямую линию в область положительных значений, находят контактную разность потенциалов (см. рис.3).

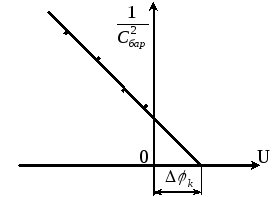
Рис.3. Определение контактной разности потенциалов