
ЫТжМС экзамен
.docx|
1 |
Ақиқат оқиға дегеніміз
|
|
|
ықтималдығы 1-ден үлкен болатын кез келген оқиға. |
|
|
ықтималдығы 1-ден кем болатын кез келген оқиға. |
|
+ |
сынақ нәтижесінде әр уақытта пайда болатын (яғни ) оқиға. |
|
|
ешуақытта пайда болмайтын оқиға. |
|
|
Дұрыс жауабы келтірілмеген |
|
|
|
|
|
|
|
2 |
Студент емтиханның 25 сұрағының 20-сын біледі. Оның емтихан алушының бір сұрағына жауап беру ықтималдығын табыңыз: |
|
|
1 |
|
|
0 |
|
|
0,1 |
|
|
0,6 |
|
+ |
0,8 |
|
|
|
|
|
|
|
3 |
А оқиғасының ықтималдығы р. қарама-қарсы оқиғаның ықтималдығы неге тең?
|
|
+ |
1-р
|
|
|
-р
|
|
|
1 |
|
|
р-1
|
|
|
0 |
|
|
|
|
|
|
|
4 |
. "машина" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
+ |
(м,а,ш,и,н) |
|
|
(м,а,н, и) |
|
|
(а,в,с,д,е) |
|
|
(р, с, к) |
|
|
(р, с, к) |
|
|
|
|
|
|
|
5 |
"фактор" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
(р, ф, к) |
|
+ |
(р, а, к, т, о, ф) |
|
|
(р, ф , к) |
|
|
(а,б,в) |
|
|
(а, о) |
|
|
|
|
|
|
|
6 |
"бизнес" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
(л,м,н) |
|
|
(и ,е) |
|
+ |
(б, з, н, с,е, и) |
|
|
(б, з,н, с) |
|
|
(б , з, н, с) |
|
|
|
|
|
|
|
7 |
"функция" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
(б, з,н, с) |
|
|
(у, и ,е) |
|
|
(л,т,н,я) |
|
+ |
(ф,у,н,к,ц,и,я) |
|
|
(б , з, н, с) |
|
|
|
|
|
|
|
8 |
"элемент" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
(б , з, н, с) |
|
|
(ф,у,т,б ) |
|
|
(л,т, а, и, ф,у,т н,я) |
|
|
(б, з,н, с) |
|
+ |
(т, н, е, м, л, э) |
|
|
|
|
|
|
|
9 |
«футбол" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
+ |
(ф,у,т,б,о,л) |
|
|
(у, и ,е) |
|
|
(л,т,н,я) |
|
|
(б, з,н, с) |
|
|
(б , з, н, с) |
|
|
|
|
|
|
|
10 |
Тиын екі рет лақтырылған. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
(ЕЕ, ЕЦ, ЦЦ) |
|
+ |
(ЕЕ, ЕЦ, ЦЕ, ЦЦ) |
|
|
(ЕЕ, ЦЦ) |
|
|
(Е, Ц) |
|
|
(ЦЕ, ЕЕ, ЦЦ) |
|
|
|
|
|
|
|
11 |
1-ден 5-ке дейінгі цифрлар жеке қағазға жазылып, қорапқа салынған. Кездейсоқ бір қағаз алынады. Осы сынаққа сәйкес келетін элементар оқиғалар кеңістігін көрсетіңіз. |
|
|
3 |
|
|
5, 4, 2, 1 |
|
+ |
1, 2, 3, 4, 5 |
|
|
1, 3, 5 |
|
|
3, 5 |
|
|
|
|
|
|
|
12 |
Кездейсоқ сандар тізбегінен кез келген сан алынған. А-алынған сан 5-ке бөлінеді; В-алынған сан 0-мен аяқталады. АВ оқиғасы нені білдіреді? |
|
|
Алынған сан 5 цифрымен аяқталмайды; |
|
|
Алынған сан 5 цифрымен аяқталады; |
|
+ |
Алынған сан 0 цифрымен аяқталады; |
|
|
Алынған сан жұп; |
|
|
Алынған сан 7 цифрымен аяқталады. |
|
|
|
|
|
|
|
13 |
Кездейсоқ оқиғаның ықтималдығы қандай шартты қанағаттандырады?
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
14 |
Екі адам бір партия шахмат ойнаған. А- бірінші ойыншы жеңеді. В- екінші ойыншы жеңеді. Толық топ құру үшін осы екі оқиғаға тағы қандай оқиға қосу керек? |
|
|
С- екеуі де жеңеді; |
|
|
Дұрыс жауабы келтірілмеген; |
|
|
С- екеуі де жеңіледі; |
|
+ |
С- екеуі тең ойнайды; |
|
|
Толық топ құру мүмкін емес. |
|
|
|
|
|
|
|
15 |
А, В, С оқиғалары бір сынаққа қатысты оқиғалар. Төмендегілердің қайсысы А және В оқиғалары орындалады, бірақ С оқиғасы орындалмайды дегенді білдіретін оқиға болады? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
А+А және АА оқиғалары нені білдіреді? |
|
|
2А |
|
|
0,5А |
|
+ |
А |
|
|
3А |
|
|
4А |
|
|
|
|
|
|
|
17 |
Толық ықтималдық формуласын көрсетіңіз. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
Әрбiр атылған оқтың нысанаға тию ықтималдығы 0,6-ға тең. 150 рет атылған оқтың нысанаға тию саны 50-ден 90-ға дейiнгі аралықта болу ықтималдығын табу үшiн қандай жуықтау формуласы қолданылады? |
|
+ |
Лапластың интегралдық теоремасы |
|
|
Толық ықтималдық формуласы |
|
|
Бернулли формуласы
|
|
|
Пуассон формуласы |
|
|
Лапластың локалдық теоремасы
|
|
|
|
|
|
|
|
19 |
Баскетболшы допты себетке түсiру ықтималдығы 0,3-ке тең. Оның алты рет лақтырған добының төртеуi себетке түсу ықтималдығын есептеу үшiн қандай формула қолданылады? |
|
|
Пуассон формуласы
|
|
|
Лапластың локалды теоремасы |
|
|
Лапластың интегралдық теоремасы |
|
|
Толық ықтималдық формуласы
|
|
+ |
Бернулли формуласы
|
|
|
|
|
|
|
|
20 |
Екi тиын 300 рет тасталды. Екi елтаңбаның 80 рет пайда болу ықтималдығын табу үшiн қандай жуықтау формуласы қолданылады? |
|
|
Толық ықтималдық формуласы |
|
+ |
Лапластың локалдық теоремасы |
|
|
Лапластың интегралдық теоремасы |
|
|
Бернулли формуласы |
|
|
Пуассон формуласы |
|
|
|
|
|
|
|
21 |
Ақиқат оқиғаның ықтималдығы неге тең? |
|
+ |
1 |
|
|
0,5 |
|
|
0 |
|
|
0,9 |
|
|
кез келген сан болуы мүмкiн |
|
|
|
|
|
|
|
22 |
Мүмкiн емес оқиғаның ықтималдығы неге тең? |
|
|
0,5 |
|
+ |
0 |
|
|
1 |
|
|
0,1 |
|
|
кез келген сан болуы мүмкiн |
|
|
|
|
|
|
|
23 |
Х кездейсоқ шамасы биномдық заң бойынша үлестiрiлген. Оның сандық сипаттамалары қандай формулалармен есептелінедi? |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
Кездейсоқ оқиғаның ықтималдығы қандай шартты қанағаттандырады? |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
25 |
Х
кездейсоқ шамасының
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
қорапта 3 ақ және 5 қара шар бар. Кездейсоқ алынған шардың ақ болу ықтималдығын тап. |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
Кiтап сөресiнде тарихтан 3 кiтап және экономикадан 7 кiтап бар. Кездейсоқ алынған кiтаптың тарих кiтабы болу ықтималдығын тап. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
Стаканда 2 жай және 5 түстi карандаштар бар. Кездейсоқ алынған карандаштың жай карандаш болу ықтималдығын тап. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
қорапта 3 ақ және 5 қызыл шарлар бар. Кездейсоқ алынған шардың қызыл болу ықтималдығын тап. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
30 |
5 тор көз және 7 жол дәптерлер бар. Кездейсоқ алынған дәптердiң тор көздi болу ықтималдығын тап. |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
31 |
15 тор көз және 9 жол дәптерлер бар. Кездейсоқ алынған дәптердiң жол дәптер болу ықтималдығын тап. |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
Алмастырудың саны қандай формуламен есептеледі? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
Орналастырудың саны қандай формуламен есептеледі? |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
Терудің саны қандай формуламен есептеледі? |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
35 |
Қайталанбалы алмастыру қандай формуламен есептеледі? |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
36 |
Қайталанбалы теру қандай формуламен есептеледі? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
Топта 4 қыз бала және 5 ер бала бар. Кездейсоқ алынған 7 студенттің ішінде 3 қыз бала болу ықтималдығын тап? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
1, 2, 3, 4, 5, 6, 7 сандарынан цифрлары қайталанбайтын төрт таңбалы қанша сан жазуға болады? |
|
|
120 |
|
+ |
840 |
|
|
720 |
|
|
640 |
|
|
2401 |
|
|
|
|
|
|
|
39 |
Жәшікте 3, 4, 5, 6 цифрлары жазылған төрт шар бір-бірден алынып, солдан оңға қарай қойылады. Сонда 5364 саны шығу ықтималдығын тап. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
А, К, И, Н, У, Л, К әріптері жазылған 7 карта бір-бірден алынып, солдан оңға қарай қойылады. Сонда "КАНИКУЛ" сөзінің шығу ықтималдығын тап. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
41 |
2, 5, 7, 8, 9 цифрларынан үш таңбалы қанша сан жазуға болады (цифрлары қайталанбайтын). |
|
|
24 |
|
|
120 |
|
|
640 |
|
|
372 |
|
+ |
60 |
|
|
|
|
|
|
|
42 |
Топта 8 адам бар. Сұраққа жауап беру үшін кездейсоқ екі адам таңдап алынған. Таңдап алудың қанша әдісі бар? |
|
|
16 |
|
|
4 |
|
|
8 |
|
+ |
28 |
|
|
58 |
|
|
|
|
|
|
|
43 |
Топтa 12 адам бар. Староста мен оның орынбасарын сайлау керек. Таңдаудың қанша әдісі бар? |
|
|
987 |
|
|
4 |
|
|
8 |
|
|
16 |
|
+ |
132 |
|
|
|
|
|
|
|
44 |
Шахмат турниріне 8 адам қатысады. Егер кез келген екі ойыншы бір партиядан ойнайтыны белгілі болса, онда турнирде барлығы қанша партия ойналуы тиіс? |
|
+ |
28 |
|
|
4 |
|
|
8! |
|
|
16 |
|
|
23 |
|
|
|
|
|
|
|
45 |
Конкурсқа қатысушы 5 адамның өнер көрсету реті жеребемен анықталады. Жеребе тастаудың қанша әртүрлі жолы бар? |
|
|
4 |
|
+ |
5! |
|
|
8! |
|
|
16 |
|
|
452 |
|
|
|
|
|
|
|
46 |
Сөреде үш томдық кітап кездейсоқ ретпен қойылған. Сөредегі кітаптарды қанша жолмен орналастыруға болады? |
|
|
8! |
|
|
4 |
|
+ |
3! |
|
|
16 |
|
|
0 |
|
|
|
|
|
|
|
47 |
Қорапта 10 бөлшек зат бар. Кездейсоқ 2 бөлшек зат алудын қанша жолы бар? |
|
|
1 |
|
|
4 |
|
|
8! |
|
|
16 |
|
+ |
45 |
|
|
|
|
|
|
|
48 |
А, Т, Р,О, К әріптері жеке карточкаларға жазылған. Бала кездейсоқ ретпен 3 карточканы алып, бір біріне тіркейді. Осылай 3 карточканы таңдап алудың қанша жолы бар ? |
|
+ |
60 |
|
|
4 |
|
|
8! |
|
|
16 |
|
|
10 |
|
|
|
|
|
|
|
49 |
Екі ойын сүйегі лақтырылған. Түскен ұпайлар қосындысы 7-ге тең болу ықтималдығын табыңдар |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
Екі ойын сүйегі лақтырылған. Түскен ұпайлар қосындысы 8, ал айырымы 4 болу ықтималдығын табыңдар. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
51 |
Монета екі рет лақтырылған. Кемінде бір герб түсу ықтималдығын табыңдар. |
|
|
0,5945 |
|
|
0,3 |
|
|
|
|
|
|
|
+ |
0,75 |
|
|
|
|
|
|
|
52 |
Жәшікте жеті нөмірленген шар бар. Біреу-біреуден ізбе-із барлық шарлар алынған. Шарлардың нөмерлері өсу ретімен шыққан болу ықтималдығын табыңдар. |
|
+ |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
53 |
Қалтада 20 тиындықтан төртеу, 10 тиындықтан жетеу бар. Кездейсоқ алынған монетаның 20 тиындық болу ықтималдығын табыңыз. |
|
+ |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
54 |
10 жарамды және 3 жарамсыз детальдан тұратын партиядан тексеруге 5 деталь алынған. Алынған детальдар арасында 1 жарамсыз деталь болуының ықтималдығын табыңыз. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
10 бірдей карточкаларда нөлден тоғызға дейін түрлі сандар жазылған. Осы карточкалардан кездейсоқ құрылған екітаңбалы сан 18-ге бөліну ықтималдығын табыңыз. |
|
+ |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
56 |
Ойын сүйегі бір рет тасталынады. Түскен ұпайдың жұп болу ықтималдығын тап. |
|
|
0,04 |
|
+ |
0,5 |
|
|
1 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
57 |
Жәшікте 1 ден 10-ға дейін сандармен белгіленген 10 шар бар. Кездейсоқ бір шар алынған. Алынған шар нөмірінің 7-ден артық болмау ықтималдығы неге тең? |
|
|
1 |
|
|
0,04 |
|
+ |
0,7 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
58 |
Жақсы араластырылған 52 картадан кездейсоқ біреуі алынған. Оның тұз болу ықтималдығы неге тең. |
|
|
0,16 |
|
|
0,04 |
|
|
0,21 |
|
+ |
|
|
|
0,96 |
|
|
|
|
|
|
|
59 |
Жақсы араластырылған 52 картадан кездейсоқ біреуі алынған. Алынған картаның түсінің қара болу ықтималдығы неге тең. |
|
|
0,96 |
|
|
0,504 |
|
|
011 |
|
|
0,156 |
|
+ |
0,5 |
|
|
|
|
|
|
|
60 |
"асыл" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы алынған әріптің дауысты болу ықтималдығын тап. |
|
|
0,04 |
|
+ |
|
|
|
1 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
61 |
"мектеп" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы алынған әріптің дауыссыз болу ықтималдығын тап. |
|
|
0,8 |
|
|
0,04 |
|
+ |
|
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
62 |
"студент" сөзінің әріптерінен кездейсоқ бір әріп таңдап алынған. Осы алынған әріптің дауысты болу ықтималдығын тап. |
|
|
0,96 |
|
|
0,5 |
|
|
0,25 |
|
|
0,16 |
|
+ |
|
|
|
|
|
|
|
|
63 |
120 билеттің 10-ында ұтыс болатын лотерея билетінің біреуін сатып алған. Сол адамның ұтуының ықтималдығы қандай? |
|
+ |
|
|
|
0,04 |
|
|
1/6 |
|
|
0,16 |
|
|
12,96 |
|
|
|
|
|
|
|
64 |
Жәшікте 12 шар бар. Оның 5-і ақ, 3-і қара, 4-і қызыл. Жәшіктен алынған шардың қызыл болу ықтималдығы қандай? |
|
|
0,25 |
|
+ |
|
|
|
1,57 |
|
|
0,16 |
|
|
|
|
|
|
|
|
|
|
65 |
Жәшікте 12 шар бар. Оның 3-і ақ, 4-і қара, 5-і қызыл. Жәшіктен алынған шардың қызыл болу ықтималдығы қандай? |
|
|
|
|
|
0,04 |
|
+ |
|
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
66 |
6 студенттен тұратын топта 3 озат. Тізім бойынша кездейсоқ 4 студент таңдап алынған. Таңдап алынғандардың ішінде 2 озат болу ықтималдығын тап. |
|
|
|
|
|
0,3 |
|
+ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
67 |
Екі тиын тасталған. Екі герб түсу ықтималдығын тап. |
|
|
|
|
|
0,3 |
|
|
|
|
+ |
|
|
|
1 |
|
|
|
|
|
|
|
68 |
Екі ойын сүйегі тасталған. Түскен ұпайлардың қосындысы үш болу ықтималдығын тап. |
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
69 |
Үш ойын сүйегін қатар лақтырғанда бірдей сандар түсуінің ықтималдығын табыңыз. |
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
70 |
Жеті қабат үйдің бірінші қабатында лифтке үш адам кірген. Олардың әрқайсысы 2-шіден бастап жоғарғы қабаттардың кез келгенінде бірдей ықтималдықпен шығуы мүмкін. Олардың барлығының 7-қабатта шығу ықтималдығын табыңдар. |
|
+ |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
|
|
Х-тің У-ке байланысты таңдамалық сызықтық емес регрессиялық теңдеуі |
|
|
Х-тің У-ке байланысты таңдамалық квадраттық регрессиялық теңдеуі |
|
+ |
У-тің Х-ке байланысты таңдамалық сызықтық регрессиялық теңдеуі |
|
|
У-тің Х-ке байланысты таңдамалық сызықтық емес регрессиялық теңдеуі |
|
|
Х-тің У-ке байланысты таңдамалық сызықтық регрессиялық теңдеуі |
|
|
|
|
|
|
|
72 |
|
|
|
Х-тің У-ке байланысты таңдамалық сызықтық емес регрессиялық теңдеуі |
|
|
Х-тің У-ке байланысты таңдамалық квадраттық регрессиялық теңдеуі |
|
|
У-тің Х-ке байланысты таңдамалық сызықтық регрессиялық теңдеуі |
|
|
У-тің Х-ке байланысты таңдамалық сызықтық емес регрессиялық теңдеуі |
|
+ |
Х-тің У-ке байланысты таңдамалық сызықтық регрессиялық теңдеуі |
|
|
|
|
|
|
|
73 |
Жәшікте 3 ақ, 3 қара шар бар. Қайтарымсыз бірінен соң бірі екі шар таңдалған. Егер бірінші шар қара екендігі белгілі болса, екінші шардың ақ болу ықтималдығын табыңдар. |
|
|
|
|
|
0,3 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
74 |
Жай болжам дегеніміз қандай болжам? |
|
+ |
Бір ғана ұйғарымнан тұратын болжам. |
|
|
Саны шектеулі немесе шексіз жай болжамдардан тұратын болжам. |
|
|
Белгісіз сипаттамалары бар болжам. |
|
|
Белгісіз сипаттамалары жоқ болжам. |
|
|
Белгісіз сипаттамалары біреу болжам. |
|
|
|
|
|
|
|
75 |
А оқиғасы В оқиғасынан тәуелсiз деп аталады, егер де: |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
76 |
А және В үйлесiмсiз оқиғалар болса, онда келесi теңдiк орындалады: |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
77 |
Ең болмағанда бiр оқиғаның пайда болу ықтималдығы қандай формула арқылы есептеледi? |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
Жәшiкте
7 стандартты және
3 стандартты емес детальдар бар.
Кездейсоқ екi
деталь алынады. А- бiрiншi
деталь стандартты, В - екiншi
деталь стандартты болды деген оқиғалар
болса, онда
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
қорапта
5 ақ және
3 қара шар бар. Кездейсоқ екi шар алынады.
А- бiрiншi шар ақ, В - екiншi шар қара болды
деген оқиғалар
болса, онда
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
Кiтап
сөресiнде
тарихтан 4 кiтап және
экономикадан 5 кiтап бар. Кездейсоқ
екi кiтап алынады. А- бiрiншi кiтап
тарихтан, В - екiншi кiтап экономикадан
болды деген оқиғалар
болса, онда
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
81 |
Жәшiкте
8 стандартты және
6 стандартты емес деталдар бар. Кездейсоқ
екi
детал алынады. А- бiрiншi
детал стандартты, В - екiншi
детал стандартты емес болды деген
оқиғалар
болса, онда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
82 |
қорапта
7 ақ және
4 қара шар бар. Кездейсоқ екi шар алынады.
А- бiрiншi шар қара, В - екiншi шар қара
болды деген оқиғалар
болса, онда
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83 |
4 қызыл және 6 жасыл карандаштары бар қораптан кездейсоқ екi карандаш түсiп қалды. Олардың екеуi де қызыл карандаш болуының ықтималдығын тап. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84 |
Жәшiкте 4 стандартты және 2 стандартты емес детальдар бар. Кездейсоқ екi деталь алынады. Олардың екеуi де стандартты болуының ықтималдығын тап. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85 |
қорапта 5 ақ және 4 қара шар бар. Кездейсоқ екi шар алынады. Олардың екеуi де қара шар болуының ықтималдығын тап. |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
86 |
4 қызыл және 6 жасыл карандаштары бар қораптан кездейсоқ екi карандаш түсiп қалды. Олардың екеуi де жасыл болуының ықтималдығын тап. |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
Жәшiкте 4 стандартты және 3 стандартты емес деталдар бар. Кездейсоқ екi детал алынады. Олардың екеуi де стандартты емес болуының ықтималдығын тап. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88 |
құрылымның бiр-бiрiнен тәуелсiз жұмыс жасайтын екi бөлшегi iстен шықпау ықтималдықтары 0,6 және 0,7 -ге тең. Тек қана бiр бөлшектің iстен шықпай қызмет жасау ықтималдығын тап. |
|
|
0,88 |
|
|
0,42 |
|
+ |
0,46 |
|
|
0,45 |
|
|
1,3 |
|
|
|
|
|
|
|
89 |
Екi зеңбiректен бiрдей оқ атылды. Бiрiншi зеңбiректен атылған оқтың нысанаға тию ықтималдығы 0,8 -ге, ал екiншiсiнiкi 0,7 -ге тең. Олардың тек қана бiреуiнiң нысанаға тию ықтималдығын тап. |
|
|
0,382 |
|
|
0,94 |
|
|
0,56 |
|
+ |
0,38 |
|
|
1,5 |
|
|
|
|
|
|
|
90 |
Бiрiншi жәшiктегi детальдардың 70 -i екiншi сортты, ал екiншi жәшiктегi детальдардың 40 -i екiншi сортты. Әрбiр жәшiктен бiр-бiрден деталь алынады. Олардың тек қана бiреуiнiң екiншi сортты болу ықтималдығын тап. |
|
|
0,57 |
|
|
1,1 |
|
|
0,82 |
|
|
0,28 |
|
+ |
0,54 |
|
|
|
|
|
|
|
91 |
Цехта жұмыс тоқтағандығын хабарлауға екi сигнализатор орнатылған. Жұмыс тоқтағанда бiрiншi сигнализатордың iске қосылу ықтималдығы 0,9, ал екiншiсiнiкi 0,8-ге тең. Жұмыс тоқтағанда олардың тек қана бiреуiнiң iске қосылу ықтималдығын тап. |
|
|
1,7 |
|
|
0,98 |
|
|
0,72 |
|
|
0,25 |
|
+ |
0,26 |
|
|
|
|
|
|
|
92 |
Екi өнеркәсiптiң іске қосылу ықтималдығы сәйкесiнше 0,2 және 0,15 -ке тең. Олардың тек қана бiреуiнiң iске қосылу ықтималдығын тап. |
|
+ |
0,29 |
|
|
0,12 |
|
|
0,17 |
|
|
0,35 |
|
|
0,32 |
|
|
|
|
|
|
|
93 |
Бiр оқ атылғанда нысанаға тию ықтималдығы 0,3-ке тең. Атылған екi оқтың кемiнде бiреуiнiң тию ықтималдығын тап. |
|
|
0,551 |
|
+ |
0,51 |
|
|
0,42 |
|
|
0,60 |
|
|
0,91 |
|
|
|
|
|
|
|
94 |
Екi тиын тасталды. Елтаңбаның кемiнде бiр рет пайда болу ықтималдығын тап. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95 |
Екi ойын сүйегi тасталды. 6 ұпайдың кемiнде бiр ойын сүйегiнде пайда болу ықтималдығын тап. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
96 |
Жоғары сортты бұйымды дайындау ықтималдығы 0,7 -ге тең. Кездейсоқ алынған екi бұйымның кемiнде бiреуi жоғары сортты болу ықтималдығын тап. |
|
|
0,42 |
|
|
0,1 |
|
+ |
0,91 |
|
|
0,21 |
|
|
0,999 |
|
|
|
|
|
|
|
97 |
Бiр лоторея билетiнде ұтыс шығу ықтималдығы 0,2 -ге тең. Кездейсоқ алынған екi билеттiң кемiнде бiреуiнде ұтыс болу ықтималдығын тап. |
|
+ |
0,36 |
|
|
0,04 |
|
|
0,32 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
98 |
Жәшікте 10 шар бар. Оның 6-ы ақ, 4-і қара. Жәшіктен кездейсоқ 2 шар алынған. 2 шардың да қара болу ықтималдығын тап. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 |
Сумкада 1-ден 6-ға дейін нөмірленген бірдей 6 доп бар. Кездейсоқ екі доп алынған. Олардың 5 және 2-ші нөмірлі шар болу ықтималдығын тап. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
Қорапта 6 қызыл, 4 көк, 2 сары қарындаш бар. Кездейсоқ 3 қарындаш алынған. Олардың әртүрлі түсті болу ықтималдығы қандай? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
Фирмада 2 аудитор, 4 программист жұмыс істейді. Командировкаға 3 адам жіберілген. Командировкаға кеткендердің ішінде 1 аудитор, 2 программист болу ықтималдығын тап. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102 |
Халық банкінің 10 бөлімшесінің 5-і қаланың ортасында орналасқан. Тексеру үшін кездейсоқ 3 банк алынған. Осылардың екеуінің қаланың орталығында орналасқан болу ықтималдығы қандай? |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
Бес билеттің екеуі ұтады. Кездейсоқ алынған екі билеттің біреуі ұтатындығының ықтималдығын табыңыз. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
104 |
10 электршамының үшеуі жарамсыз. Кездейсоқ екі шам алынған. Осы екі шам да жарамсыз болу ықтималдығын табыңыз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
105 |
Бес билеттің екеуі ұтады. Кездейсоқ алынған екі билеттің кемінде біреуі ұтатындығының ықтималдығын табыңыз. |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
106 |
Ойын сүйегі бір рет тасталынады. Түскен ұпайдың тақ болу ықтималдығын тап. |
|
|
0,04 |
|
+ |
0,5 |
|
|
1 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
107 |
Жәшікте 1 ден 10-ға дейін сандармен белгіленген 10 шар бар. Кездейсоқ бір шар алынған. Алынған шар нөмірінің 4-тен артық болмау ықтималдығы неге тең? |
|
|
1 |
|
|
0,04 |
|
+ |
0,4 |
|
|
0,16 |
|
|
0,96 |
|
|
|
|
|
|
|
108 |
Екі жәшікке детальдар салынған. Біріншісінде- 5, оның ішінде екеуі жарамсыз, екіншісінде- 8, оның ішінде үшеуі жарамсыз. Әр жәшіктен кездейсоқ бір детальдан алынады. Алынған детальдардың екеуі де жарамды болу ықтималдығын табыңыз. |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109 |
Екі мерген нысанаға бір оқтан атады. Біріншісінің тигізу ықтималдығы 0,7; екіншісінікі- 0,6. Нысанаға бір оқ тигендігінің ықтималдығын табыңыз. |
|
|
0,16 |
|
|
0,8 |
|
|
0,65 |
|
+ |
0,46 |
|
|
0,96 |
|
|
|
|
|
|
|
110 |
Үш мерген нысанаға бір оқтан атады. Біріншісінің тигізу ықтималдығы 0,5; екіншісінікі- 0,6; үшіншісінікі-0,7. Нысанаға бір де бір оқ тимегендігінің ықтималдығын табыңыз. |
|
|
0,56 |
|
|
0,83 |
|
|
0,65 |
|
|
0,16 |
|
+ |
0,06 |
|
|
|
|
|
|
|
111 |
Бұйымның жарамды болу ықтималдығы 0,8. Екі бұйымның арасында ең болмағанда бір жарамды болуының ықтималдығын табыңыз. |
|
|
0,42 |
|
+ |
0,96 |
|
|
1 |
|
|
0,81 |
|
|
0,75 |
|
|
|
|
|
|
|
112 |
Бірінші поездың кешігу ықтималдығы 0,2; ал екіншісінікі 0,64. Екі поезд да кешігуінің ықтималдығын тап. |
|
|
0,321 |
|
+ |
0,128 |
|
|
0,413 |
|
|
0,285 |
|
|
0,568 |
|
|
|
|
|
|
|
113 |
Бірінші студенттің емтиханды тапсыра алмау ықтималдығы 0,3; ал екіншісінікі 0,5. Тек қана бір студенттің емтихан тапсыра алмау ықтималдығын тап. |
|
|
0,4 |
|
|
0,32 |
|
+ |
0,5 |
|
|
0,12 |
|
|
1 |
|
|
|
|
|
|
|
114 |
Баспахана екі почта бөлімшесіне газеттер жіберді. Бірінші бөлімшеге өз уақытында газеттің жету ықтималдығы 0,9; ал екіншісінікі- 0,8. Тек қана бір бөлімшенің өз уақытында газетті алу ықтималдығын тап. |
|
|
0,4 |
|
|
0,32 |
|
+ |
0,26 |
|
|
0,128 |
|
|
0 |
|
|
|
|
|
|
|
115 |
Студент өзіне керек формуланы екі кітаптан іздейді. Формула бірінші кітаптан табылу ықтималдығы 0,6-ға, ал екіншісінен табылу ықтималдығы 0,8-ге тең. Формуланың тек бір кітаптан табылу ықтималдығын тап. |
|
|
0,128 |
|
|
0,32 |
|
|
0,45 |
|
+ |
0,44 |
|
|
2 |
|
|
|
|
|
|
|
116 |
Екі пәннің әрқайсысынан студенттердің бақылау жұмысын өз уақытында орындау ықтималдығы сәйкесінше 0,5 және 0,6. Екі пәннен де студенттердің бақылау жұмысын өз уақытында орындау ықтималдығын тап. |
|
|
0258 |
|
|
0,32 |
|
|
0,14 |
|
|
0,12 |
|
+ |
0,30 |
|
|
|
|
|
|
|
117 |
Техникалық бақылау бөлімі бұйымның стандарттығын тексереді. Бұйымның стандарт болу ықтималдығы 0,9. Тексерілген екі бұйымның тек қана біреуінің стандартты болу ықтималдығын тап. |
|
+ |
0,18 |
|
|
0,32 |
|
|
0,4 |
|
|
0,128 |
|
|
4 |
|
|
|
|
|
|
|
118 |
Баспахана екі почта бөлімшесіне газеттер жіберді. Бірінші бөлімшеге өз уақытында газеттің жету ықтималдығы 0,9; ал екіншісінікі- 0,8. Тек қана бір бөлімшенің өз уақытында газетті алу ықтималдығын тап. |
|
+ |
0,26 |
|
|
0,42 |
|
|
0,18 |
|
|
0,64 |
|
|
0,012 |
|
|
|
|
|
|
|
119 |
Баспахана екі почта бөлімшесіне газеттер жіберді. Бірінші бөлімшеге өз уақытында газеттің жету ықтималдығы 0,7; ал екіншісінікі- 0,8. Тек қана бір бөлімшенің өз уақытында газетті алу ықтималдығын тап. |
|
+ |
0,38 |
|
|
0,32 |
|
|
0,26 |
|
|
0,128 |
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
Математикалық күтімді |
|
+ |
Орташа квадраттық ауытқуды
|
|
|
Дисперсияны
|
|
|
Ықтималдықты
|
|
|
Үлестірімділік функцияны |
|
|
|
|
|
|
|
121 |
Бейес формуласын тап. |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
122 |
|
|
|
Математикалық күтімді |
|
|
Орташа квадраттық ауытқуды
|
|
|
Дисперсияны
|
|
|
Ықтималдықты
|
|
+ |
Үлестірімділік тығыздықты |
|
|
|
|
|
|
|
123 |
Цехта жұмыс тоқтағандығын хабарлауға екi дабыл беруші орнатылған. Жұмыс тоқтағанда бiрiншi дабыл берушінің iске қосылу ықтималдығы 0,9, ал екiншiсiнiкi 0,8-ге тең. Жұмыс тоқтағанда олардың екеуiнiң де iске қосылу ықтималдығын табыңыз. |
|
|
0,25 |
|
|
0,98 |
|
+ |
0,72 |
|
|
0,26 |
|
|
1,7 |
|
|
|
|
|
|
|
124 |
Радиошам үш партияның біріне, сәйкесінше, 0,25; 0,5 және 0,25 ықтималдықтарымен жатуы мүмкін. Радиошам белгіленген уақыт жұмыс істеу ықтималдығы әр партия үшін, сәйкесінше 0,1; 0,2; және 0,4. Алынған кез келген бір радиошамның белгіленген уақыт жұмыс істеу ықтималдығын табыңыз. |
|
|
0,65 |
|
|
0,325 |
|
+ |
0,225 |
|
|
0,425 |
|
|
0,465 |
|
|
|
|
|
|
|
125 |
|
|
|
Математикалық күтімді |
|
|
Орташа квадраттық ауытқуды
|
|
+ |
Дисперсияны
|
|
|
Ықтималдықты
|
|
|
Үлестірімділік функцияны |
|
|
|
|
|
|
|
126 |
Қарама-қарсы оқиғалардың ықтималдықтарының қосындысы неге тең? |
|
|
0 |
|
|
-1 |
|
+ |
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
127 |
Байес формуласын көрсет |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
Дұрыс жауабы келтірілмеген |
|
|
|
|
|
|
|
128 |
Х
кездейсоқ шамасы
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
129 |
|
|
|
Математикалық күтімді |
|
|
Орташа квадраттық ауытқуды
|
|
+ |
Дисперсияны
|
|
|
Ықтималдықты
|
|
|
Үлестірімділік функцияны |
|
|
|
|
|
|
|
130 |
Дискретті кездейсоқ шаманың математикалық күтімі мынадай формуламен анықталады: |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
131 |
Үзіліссіз кездейсоқ шаманың математикалық күтімі мынадай формуламен анықталады: |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
132 |
|
|
|
Толық ықтималдық |
|
|
Бейес формуласы |
|
+ |
Бернулли |
|
|
Лапластың интегралдық теоремасы |
|
|
Лапластың локалдық теоремасы
|
|
|
|
|
|
|
|
133 |
|
|
|
Лапластың локалды теоремасы |
|
|
Бернулли формуласы |
|
|
Пуассон формуласы
|
|
+ |
Ең
ықтималды санды табу формуласы |
|
|
Толық ықтималдық формуласы |
|
|
|
|
|
|
|
134 |
|
|
|
Лапластың интегралдық теоремасы |
|
|
Бернулли формуласы |
|
+ |
Пуассон формуласы |
|
|
Лапластың локалдық теоремасы
|
|
|
Толық ықтималдық формуласы |
|
|
|
|
|
|
|
135 |
|
|
+ |
Ықтималдықты |
|
|
Математикалық күтімді
|
|
|
Дисперсияны |
|
|
Орташа квадраттық ауытқуды |
|
|
Үлестірімділік функцияны |
|
|
|
|
|
|
|
136 |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
137 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
138 |
Жау А, В, С типті ракеталарын сәйкесінше 0,4; 0,7; 0,2 ықтималдықтарымен қолдана алады. Ракетаны қирату ықтималдығы сәйкесінше 0,5; 0,7; 0,8. Егер жау бір типті ракетадан біреуін қолданғаны белгілі болса, осы ракета қиратылатындығының ықтималдығын табыңыз. |
|
|
0,571 |
|
|
0,4125 |
|
+ |
0,85 |
|
|
0,8125 |
|
|
0,3125 |
|
|
|
|
|
|
|
139 |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
Баскетболшының допты корзинаға түсiру ықтималдығы 0,7-ке тең. Оның жеті рет лақтырған добының үшеуi корзинаға түсу ықтималдығын есептеу үшiн қандай формула қолданылады? |
|
|
Пуассон формуласы |
|
+ |
Бернулли формуласы |
|
|
Лапластың локалды теоремасы |
|
|
Лапластың интегралдық теоремасы |
|
|
Толық ықтималдық формуласы |
|
|
|
|
|
|
|
141 |
Екi тиын 400 рет тасталды. Екi елтаңбасының 90 рет пайда болу ықтималдығын табу үшiн қандай жуықтау формуласы қолданылады? |
|
|
Пуассон формуласы |
|
|
Бернулли формуласы |
|
+ |
Лапластың локалды теоремасы |
|
|
Лапластың интегралдың теоремасы |
|
|
Толық ықтималдық формуласы |
|
|
|
|
|
|
|
142 |
Әрбiр атылған оқтың нысанаға тию ықтималдығы 0,5-ке тең. 160 рет атылған оқтың нысанаға тию саны 45-тен 90-ға дейiнгі аралықта болу ықтималдығын табу үшiн қандай жуықтау формуласы қолданылады? |
|
|
Лапластың локалды теоремасы |
|
|
Бернулли формуласы |
|
|
Пуассон формуласы |
|
+ |
Лапластың интегралдық теоремасы |
|
|
Толық ықтималды формуласы |
|
|
|
|
|
|
|
143 |
Әрбiр атылған оқтың нысанаға тию ықтималдығы p-ға тең. Үш рет атылған оқтың екеуi нысанаға тию ықтималдығы неге тең? |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
144 |
Екi өнеркәсiптiң іске қосылу ықтималдығы сәйкесiнше 0,2 және 0,15 -ке тең. Олардың екеуiнiң де iске қосылу ықтималдығын табыңыз. |
|
+ |
0,03 |
|
|
0,12 |
|
|
0,17
|
|
|
0,35 |
|
|
0,29 |
|
|
|
|
|
|
|
145 |
Тиынды 14 рет тастағанда елтаңбаның пайда болуының ең ықтимал санын тап. |
|
|
8 |
|
+ |
7 |
|
|
7,5 |
|
|
6 |
|
|
6,5 |
|
|
|
|
|
|
|
146 |
Лақтырылған доптың корзинаға түсу ықтималдығы 0,8-ге тең. 11 рет лақтырылған доптың ең ықтимал пайда болуының санын тап. |
|
|
8,8 |
|
|
8 |
|
+ |
9 |
|
|
9,6 |
|
|
10 |
|
|
|
|
|
|
|
147 |
Жоғары сортты бұйымды дайындау ықтималдығы 0,7 -ге тең. Кездейсоқ алынған 13 бұйымның iшiнде жоғары сортты бұйымдардың ең ықтимал пайда болуының санын тап. |
|
|
10 |
|
|
9,1 |
|
|
9,8 |
|
+ |
9 |
|
|
8,8 |
|
|
|
|
|
|
|
148 |
Студент тесттiң әр сұрағына дұрыс жауап беру ықтималдығы 0,2 -ге тең. 31 сұраққа берiлген дұрыс жауаптың ең ықтимал пайда болуының санын тап. |
|
|
7 |
|
|
6,2 |
|
|
5,2 |
|
|
5 |
|
+ |
6 |
|
|
|
|
|
|
|
149 |
Нысанаға атылған әрбiр оқтың тию ықтималдығы 0,9 -ға тең. Атылған 12 оқтың нысанаға тиюiнiң ең ықтимал санын тап. |
|
+ |
11 |
|
|
10 |
|
|
10,7 |
|
|
12 |
|
|
11,7 |
|
|
|
|
|
|
|
150 |
10 тәуелсiз сынақта құралдың iстен шығу саны - Х кездейсоқ шамасы үшiн М(Х)=3. Әрбiр сынақта құралдың iстен шығу ықтималдығы бiрдей болса, оның дисперсиясы қандай? |
|
|
20,1 |
|
|
0,21 |
|
|
20,3 |
|
+ |
2,1 |
|
|
1,8 |
|
|
|
|
|
|
|
151 |
Тиынды үш рет лақтырамыз. Гербтің түсуі екі реттен кем болмайтындығының ықтималдығын табыңыз. |
|
|
0,8 |
|
+ |
0,5 |
|
|
0,625 |
|
|
1,16 |
|
|
0,96 |
|
|
|
|
|
|
|
152 |
Сигнал бергенде бір таңбаның дұрыс берілмеу ықтималдығы р. Берілген он таңбаның ішінде дәл біреуі дұрыс берілмеген болу ықтималдығын табыңдар. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
153 |
Ойын сүйегі үш рет лақтырамыз. Бірлік дәл үш рет түсті деген оқиғаның ықтималдығын табыңыз. |
|
|
|
|
|
0,3 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
154 |
Үш ойын сүйегі лақтырылған. Осы сынақты 5 рет тәуелсіз қайталағанда 2 рет үш бірлік ұпай түсу ықтималдығын табыңдар. |
|
|
1 |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155 |
Ақиқат оқиға дегеніміз
|
|
|
ықтималдығы 1-ден үлкен болатын кез келген оқиға. |
|
|
ықтималдығы 1-ден кем болатын кез келген оқиға. |
|
+ |
сынақ нәтижесінде әруақытта пайда болатын (яғни ) оқиға. |
|
|
ешуақытта пайда болмайтын оқиға. |
|
|
Дұрыс жауабы келтірілмеген |
|
|
|
|
|
|
|
156 |
Егер оқиғаның әр сынақта пайда болу ықтималдығы 0,2 болса, 400 сынақта оқиға 112 рет пайда болуының ықтималдығын жуықтап есепте. |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
157 |
Үлестірім заңы келесі қатарымен берілген кездейсоқ шамасының дисперсиясы неге тең?
|
|
+ |
0,76 |
|
|
0,6 |
|
|
0,5 |
|
|
0,90 |
|
|
52 |
|
|
|
|
|
|
|
158 |
Бернулли формуласын көрсет |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
159 |
Пуассон формуласын көрсет |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
160 |
Муавр-Лапластың төңіректік формуласы қай теңдікпен берілген? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
161 |
Муавр-Лапластың интегралдық формуласы қай теңдікпен берілген? |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
162 |
Тиын 4 рет тасталған. 2 рет елтаңба түсу ықтималдығы қандай? |
|
|
|
|
|
0,3 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
163 |
Тиын 4 рет тасталған. 3 рет елтаңба түсу ықтималдығы қандай? |
|
|
|
|
+ |
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
164 |
Ойын сүйегі 4 рет тасталған. Үш ұпайының 2 рет түсу ықтималдығы қандай? |
|
|
|
|
|
|
|
+ |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
165 |
Хабар бергенде бір әріптің бұзылу ықтималдығы 0.2-ге тең. 4 белгіден тұратын хабардың бұзылмай жету ықтималдығы қандай? |
|
|
0,16 |
|
|
0,83 |
|
|
0,65 |
|
+ |
0,4096 |
|
|
0,56 |
|
|
|
|
|
|
|
166 |
Жанұяда 4 бала бар. Ұл және қыз туылу ықтималдығы бірдей деп алып, жанұяда 2 ұл және 2 қыз болу ықтималдығын тап. |
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
+ |
|
|
|
|
|
|
|
|
167 |
Оқты бір рет атқанда нысанаға тию ықтималдығы 0,6-ға тең. 4 рет оқ атылған. Дәл екі рет нысанаға тию ықтималдығын тап. |
|
+ |
0,3456 |
|
|
0,8325 |
|
|
0,6523 |
|
|
1,162 |
|
|
0,5624 |
|
|
|
|
|
|
|
168 |
Монета тәуелсіз 2 рет лақтырылғанда кемінде бір рет елтаңба түскен болу ықтималдығын табыңдар. |
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
+ |
|
|
|
|
|
|
|
|
169 |
Сигнал бергенде бір таңбаның дұрыс берілмеу ықтималдығы р. Берілген бес таңбаның ішінде дәл біреуі дұрыс берілмеген болу ықтималдығын табыңдар. |
|
+ |
|
|
|
р |
|
|
|
|
|
|
|
|
1-р |
|
|
|
|
|
|
|
170 |
Бұйымның жарамды болу ықтималдығы 0,8. Үш бұйымның арасында жарамсыздар саны бірден артпауының ықтималдығын табыңыз. |
|
+ |
0,896 |
|
|
0,425 |
|
|
0,468 |
|
|
0,812 |
|
|
0,715 |
|
|
|
|
|
|
|
171 |
Бір атқанда ондыққа тигізу ықтималдығы 0,8. 4 рет оқ атқанда ондыққа бір рет тигізу ықтималдығын тап. |
|
|
0,7 |
|
+ |
0,0256 |
|
|
1 |
|
|
0,9984 |
|
|
0,55 |
|
|
|
|
|
|
|
172 |
Егер
|
|
|
Бірқалыпты |
|
|
Геометриялық |
|
|
Биномды |
|
+ |
Пуассондық |
|
|
Гипергеометриялық |
|
|
|
|
|
|
|
173 |
Дискреттік кездейсоқ шаманың математикалық үміті қай өрнекпен анықталады? |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
174 |
Дискреттік кездейсоқ шаманың дисперсиясы қай өрнекпен анықталады? |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
175 |
|
|
|
Орта мән |
|
|
Дисперсия; |
|
+ |
Орташа квадраттық ауытқу; |
|
|
Математикалық күтім; |
|
|
Dұрыс жауабы келтірілмеген. |
|
|
|
|
|
|
|
176 |
Параметрі болатын Пуассон заңымен берілген кездейсоқ шамасының математикалық үміті неге тең? |
|
|
0 |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
177 |
Параметрі болатын Пуассон заңымен берілген кездейсоқ шамасының дисперсиясы неге тең? |
|
|
0 |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
178 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. р1 ықтималдығын тап.
|
|
+ |
0,5 |
|
|
0,3 |
|
|
0,4 |
|
|
0,2 |
|
|
0,6 |
|
|
|
|
|
|
|
179 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. р3 ықтималдығын тап.
|
|
|
0,6 |
|
|
0,2 |
|
|
0,4 |
|
|
0,5 |
|
+ |
0,3 |
|
|
|
|
|
|
|
180 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. р1 ықтималдығын тап.
|
|
|
0,4 |
|
|
0,2 |
|
|
0,3 |
|
+ |
0,6 |
|
|
0,5 |
|
|
|
|
|
|
|
181 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. р2 ықтималдығын тап.
|
|
|
0,2 |
|
|
0,3 |
|
|
0,1 |
|
+ |
0,5 |
|
|
0,4 |
|
|
|
|
|
|
|
182 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. Оның математикалық үмiтін тап.
|
|
|
2,2 |
|
|
2,38 |
|
+ |
4 |
|
|
0,58 |
|
|
3 |
|
|
|
|
|
|
|
183 |
Х дискреттiк кездейсоқ шамасының үлестiрiм заңы кесте арқылы берiлген. Оның математикалық үмiтін тап.
|
|
|
5,5 |
|
+ |
6 |
|
|
5 |
|
|
1,14 |
|
|
0,24 |
|
|
|
|
|
|
|
184 |
Х дискреттiк кездейсоқ шамасының дисперсиясын тап.
|
|
|
1,3 |
|
|
0,31 |
|
+ |
0,21 |
|
|
1,9 |
|
|
0,82 |
|
|
|
|
|
|
|
185 |
Х дискреттiк кездейсоқ шамасының дисперсиясын тап.
|
|
+ |
0,96 |
|
|
1,8 |
|
|
1,04 |
|
|
2,4 |
|
|
4,2 |
|
|
|
|
|
|
|
186 |
Х дискреттiк кездейсоқ шамасының дисперсиясын тап.
|
|
+ |
0,84 |
|
|
3,4 |
|
|
1,04 |
|
|
0,97 |
|
|
0,3 |
|
|
|
|
|
|
|
187 |
Х дискреттiк кездейсоқ шамасының дисперсиясын тап.
|
|
|
4,16 |
|
|
1,4 |
|
|
0,14 |
|
|
2,2 |
|
+ |
0,24 |
|
|
|
|
|
|
|
188 |
Х кездейсоқ шамасы биномдық заң бойынша берiлген. Оның сандық сипаттамалары қандай формуламен есептеледi? |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
189 |
10 тәуелсiз сынақта құралдың iстен шығу саны-Х кездейсоқ шамасы үшiн М(Х)=3. Әрбiр сынақта құралдың iстен шығу ықтималдығы бiрдей болса, оның дисперсиясын тап. |
|
+ |
2,1 |
|
|
0,21 |
|
|
20,3 |
|
|
0,9 |
|
|
1,8 |
|
|
|
|
|
|
|
190 |
Тиынды лақтырғанда екеуінде де елтаңбаның түсу саны - Х кездейсоқ шамасының математикалық үмiті 12-ге тең болуы үшiн екi тиынды қанша рет тастау керек? |
|
|
12 |
|
|
16 |
|
|
8 |
|
|
24 |
|
+ |
48 |
|
|
|
|
|
|
|
191 |
Әрбiр атылған оқтың нысанаға тию ықтималдығы 0,4-ке тең. Нысанаға тиген оқ саны - Х кездейсоқ шамасының дисперсиясы 6-ға тең болуы үшiн қанша оқ атылуы керек. |
|
+ |
25 |
|
|
30 |
|
|
35 |
|
|
40 |
|
|
48 |
|
|
|
|
|
|
|
192 |
Бiр лоторея билетiнде ұтыс шығу ықтималдығы 0,2 -ге тең. Алынған билеттердегi ұтыс саны-Х кездейсоқ шамасының математикалық үмiті 10-ға тең болуы үшiн қанша билет сатып алу керек. |
|
|
5 |
|
|
10 |
|
|
20 |
|
|
30 |
|
+ |
50 |
|
|
|
|
|
|
|
193 |
Екi тиын 16 рет тасталды. Екi елтаңбаның шығу саны - Х кездейсоқ шамасының дисперсиясын тап. |
|
|
|
|
|
1 |
|
|
2 |
|
|
44 |
|
+ |
3 |
|
|
|
|
|
|
|
194 |
|
|
+ |
7 |
|
|
10 |
|
|
13 |
|
|
2 |
|
|
20 |
|
|
|
|
|
|
|
195 |
|
|
|
27 |
|
|
9 |
|
+ |
10 |
|
|
28 |
|
|
20 |
|
|
|
|
|
|
|
196 |
|
|
|
35 |
|
+ |
23 |
|
|
100 |
|
|
103 |
|
|
201 |
|
|
|
|
|
|
|
197 |
|
|
+ |
12 |
|
|
7 |
|
|
10 |
|
|
20 |
|
|
50 |
|
|
|
|
|
|
|
198 |
|
|
|
6 |
|
|
4 |
|
+ |
5 |
|
|
12 |
|
|
20 |
|
|
|
|
|
|
|
199 |
Кездейсоқ шаманы С санына көбейткенде оның математикалық үмiті қалай өзгередi? |
|
+ |
С санына еселенедi |
|
|
С санына өседi |
|
|
С санына кемидi |
|
|
|
|
|
өзгермейдi |
|
|
|
|
|
|
|
200 |
|
|
|
11 |
|
|
12 |
|
|
17 |
|
|
18 |
|
+ |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|





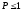






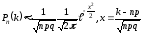
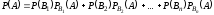

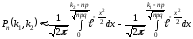
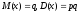
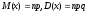



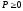

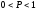


 үлестірімділік
функциясы
қандай мәндер қабылдайды?
үлестірімділік
функциясы
қандай мәндер қабылдайды?

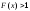

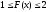



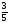




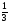

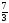





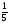


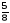


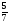



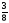

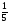


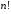

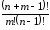

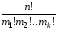


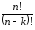


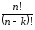


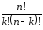
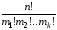

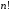




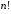
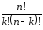







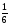
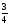


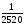




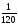

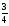




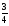

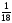


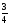
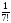





 ;
;
 ;
;

 ;
;

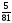



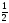
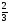





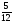




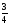







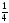




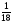
 теңдеуі
қандай
регрессиялық
теңдеу?
теңдеуі
қандай
регрессиялық
теңдеу? теңдеуі
қандай
регрессиялық
теңдеу?
теңдеуі
қандай
регрессиялық
теңдеу?
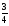

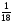




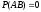
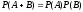









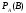 шартты
ықтималдығын
тап.
шартты
ықтималдығын
тап.
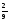



 шартты
ықтималдығын
тап.
шартты
ықтималдығын
тап.


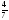

 шартты
ықтималдығын
тап.
шартты
ықтималдығын
тап.




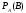 шартты
ықтималдығын
тап.
шартты
ықтималдығын
тап.

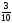
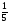
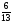
 шартты
ықтималдығын
тап.
шартты
ықтималдығын
тап.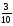



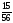
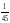







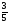
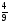



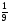
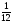


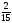










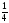




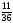

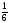

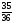
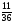



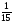

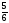



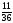

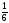



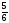


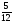

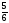







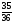






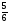

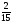

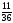


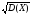 нені
анықтайды?
нені
анықтайды?




 нені
анықтайды?
нені
анықтайды? нені
анықтайды?
нені
анықтайды?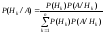 ;
;

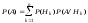

 аралығынан
мәндерді қабылдайтындығының
ықтималдығын табу формуласын көрсетіңіз:
аралығынан
мәндерді қабылдайтындығының
ықтималдығын табу формуласын көрсетіңіз:


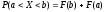

 нені
анықтайды?
нені
анықтайды?
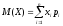


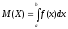

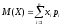
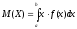
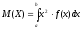
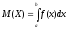
 формуласы
қалай аталады?
формуласы
қалай аталады?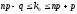 формуласы
қалай аталады?
формуласы
қалай аталады?
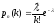 формуласы
қалай аталады?
формуласы
қалай аталады? формуласымен
нені анықтайды?
формуласымен
нені анықтайды? аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың математикалық күтімін табу
формуласын көрсетіңіз.
аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың математикалық күтімін табу
формуласын көрсетіңіз.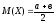


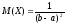
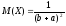
 аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың дисперсиясын табу формуласын
көрсетіңіз.
аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың дисперсиясын табу формуласын
көрсетіңіз.




 аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың ықтималдық тығыздығын табу
формуласын көрсетіңіз.
аралығында
бірқалыпты үлестірілген кездейсоқ
шаманың ықтималдық тығыздығын табу
формуласын көрсетіңіз.







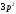




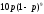





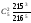

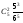
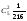

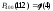





 ,
,

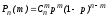
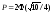





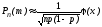


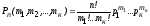

 ,
,

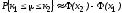

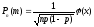


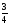






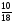














 , мұндағы
, мұндағы
 болса, кездейсоқ шама қандай үлестіріммен
берілген?
болса, кездейсоқ шама қандай үлестіріммен
берілген?
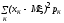









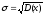 шамасы
қалай аталады?
шамасы
қалай аталады?

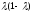

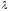


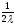










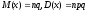





 екендiгi
белгiлi.
екендiгi
белгiлi.
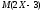 -дi
тап.
-дi
тап.
 екендiгi
белгiлi.
екендiгi
белгiлi.
 -дi тап.
-дi тап.
 екендiгi
белгiлi.
екендiгi
белгiлi.
 -дi
тап.
-дi
тап. екендiгi
белгiлi.
екендiгi
белгiлi.
 -дi тап.
-дi тап.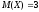 екендiгi
белгiлi.
екендiгi
белгiлi.
 -дi
тап.
-дi
тап.
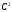 санына
еселенедi
санына
еселенедi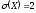 екендiгi
белгiлi.
екендiгi
белгiлi.
 -дi
тап.
-дi
тап.