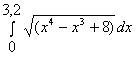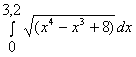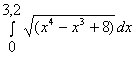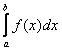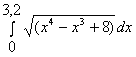3. Формулы прямоугольников

Существует несколько видов формул прямоугольников:

1. "Формула левых прямоугольников.

В общем виде формула левых прямоугольниковна отрезке[x₀;x_n]выглядит следующим образом(21):

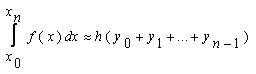
В данной формуле x₀=a, x_n=b, так как любой интеграл в общем виде выглядит: (см. формулу18).

h можно вычислить по формуле 19.

y₀, y₁,..., y_n-1- это значения соответствующей функции f(x) в точкахx₀, x₁,..., x_n-1(x_i=x_i-1+h).

2. Формула правых прямоугольников.

В общем виде формула правых прямоугольниковна отрезке[x₀;x_n]выглядит следующим образом(22):

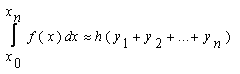
В данной формуле x₀=a, x_n=b(см. формулу для левых прямоугольников).

h можно вычислить по той же формуле, что и в формуле для левых прямоугольников.

y₁, y₂,..., y_n- это значения соответствующей функции f(x) в точкахx₁, x₂,..., x_n(x_i=x_i-1+h).

3. Формула средних прямоугольников.

В общем виде формула средних прямоугольниковна отрезке[x₀;x_n]выглядит следующим образом(23):

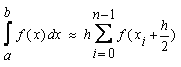
Где x_i=x_i-1+h.

В данной формуле, как и в предыдущих, требуется h умножать сумму значений функции f(x), но уже не просто подставляя соответствующие значения x₀,x₁,...,x_n-1в функцию f(x), а прибавляя к каждому из этих значенийh/2(x₀+h/2, x₁+h/2,..., x_n-1+h/2), а затем только подставляя их в заданную функцию.

h можно вычислить по той же формуле, что и в формуле для левых прямоугольников." [6]

На практике данные способы реализуются следующим образом:

a) Вычислить интеграл
по формуле левых прямоугольников при n=10, используя:

1. Mathcad;

2. Excel.

b) Вычислить интеграл
по формуле правых прямоугольников при n=10, используя:

1. Mathcad;

2. Excel.

c) Вычислить интеграл
по формуле средних прямоугольников при n=10, используя:

Для того, чтобы вычислить интеграл по формуле средних прямоугольников в Excel, необходимо выполнить следующие действия:

1. Продолжить работу в том же документе, что и при вычислении интеграла по формулам левых и правых прямоугольников.

2. В ячейку E6 ввести текст xi+h/2, а в F6 - f(xi+h/2).

3. Ввести в ячейку E7 формулу =B7+$B$4/2, скопировать эту формулу методом протягивания в диапазон ячеек E8:E16

4. Ввести в ячейку F7 формулу =КОРЕНЬ(E7^4-E7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек F8:F16

5. Ввести в ячейку F18 формулу =СУММ(F7:F16).

6. Ввести в ячейку F19 формулу =B4*F18.

7. Ввести в ячейку F20 текст средних.

В итоге получаем следующее:

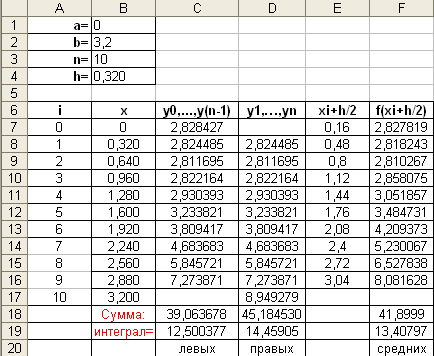
Ответ: значение заданного интеграла равно 13,40797.

Исходя из полученных результатов, можно сделать вывод, что формула средних прямоугольников является наиболее точной, чем формулы правых и левых прямоугольников.

1. Метод Монте-Карло

"Основная идея метода Монте-Карло заключается в многократном повторении случайных испытаний. Характерной особенностью метода Монте-Карло является использование случайных чисел (числовых значений некоторой случайной величины). Такие числа можно получать с помощью датчиков случайных чисел. Например, в языке программирования Turbo Pascal имеется стандартная функция random , значениями которой являются случайные чис¬ла, равномерно распределенные на отрезке [0; 1]. Сказанное означает, что если разбить указанный отрезок на некоторое число равных интервалов и вычислить значение функции random большое число раз, то в каждый интервал попадет приблизительно одинаковое количество случайных чисел. В языке программирования basin подобным датчиком является функция rnd. В табличном процессоре MS Excel функция СЛЧИС возвращает равномерно распределенное случайное число большее или равное 0 и меньшее 1 (изменяется при пересчете)" [7].

Рассмотрим интеграл:

Для того чтобы его вычислить, необходимо воспользоваться формулой ():

, где (i=1, 2, …, n) – случайные числа, лежащие в интервале [a;b].

Для получения таких чисел на основе последовательности случайных чисел x_i , равномерно распределенных в интервале [0;1], достаточно выполнить преобразование x_i=a+(b-a)x_i.

На практике данный способ реализуется следующим образом:

Вычислить интеграл

по формуле трапеций при n=10, используя:

Для того, чтобы вычислить интеграл методом Монте-Карло в Excel, необходимо выполнить следующие действия:

1. В ячейку B1 ввести текст n=.

2. В ячейку B2 ввести текст a=.

3. В ячейку B3 ввести текст b=.

В ячейку C1 ввести число 10.

4. В ячейку C2 ввести число 0.

5. В ячейку C3 ввести число 3,2.

6. В ячейку A5 ввести I, в В5 – xi, в C5 – f(xi).

7. Ячейки A6:A15 заполнить числами 1,2,3, …,10 – так как n=10.

8. Ввести в ячейку B6 формулу =СЛЧИС()*3,2 (происходит генерация чисел в диапазоне от 0 до 3,2), скопировать эту формулу методом протягивания в диапазон ячеек В7:В15.

9. Ввести в ячейку C6 формулу =КОРЕНЬ(B6^4-B6^3+8), скопировать эту формулу методом протягивания в диапазон ячеек C7:C15.

10. Ввести в ячейку B16 текст «сумма», в B17 – «(b-a)/n», в B18 – «I=».

11. Вести в ячейку C16 формулу =СУММ(C6:C15).

12. Вести в ячейку C17 формулу =(C3-C2)/C1.

13. Вести в ячейку C18 формулу =C16*C17.

В итоге получаем:

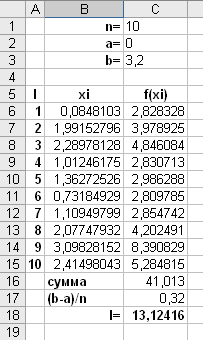
Ответ: значение заданного интеграла равно 13,12416.