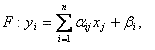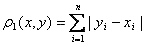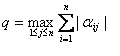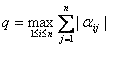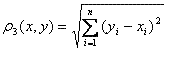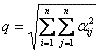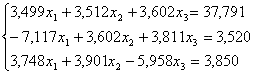4. Метод итераций
"Систему вида (12) приведем к равносильной ей системе вида x=Ax. В развернутом виде новая система выглядит так:
|
|
(15) |
Правая часть системы определяет отображение
|
|
(16) |
Это отображение преобразует точку x(x1,x2,...,xn ) n- мерного пространства в точку y(y1,y2,...,yn ) этого же пространства. Выбрав начальную точку x0(x00,...,xnn ) и подставив ее координаты в правую часть системы (15), можно построить итерационную последовательность: x0, x1,..., xn.
Условия, при выполнении которых отображение (16) будет сжимающим представлены в таблице:
|
Метрика |
Условия сходимости |
|
|
(суммирование коэффициентов по столбцам) |
|
|
(суммирование коэффициентов по строкам) |
|
|
|
При этом число q должно быть меньше единицы"[1]. ''Формула, позволяющая устанавливать момент прекращения итерационного процесса при достижении заданной точности результата:"[7]
Где
На практике данный способ реализуется следующим образом:
|
Решить систему уравнений: |
|
методом Гаусса в: |
Mathcad;
Excel.
Для того чтобы решить данную систему уравнений в Excel, нужно выполнить следующие действия:
Ячейки A1:E4 заполнить следующим образом:
Над данной системой выполнить элементарные преобразования, чтобы получить систему, у которой диагональные коэффициенты по модулю больше других коэффициентов соответствующей строки:
Для того чтобы получить первое уравнение новой системы, нужно из второго уравнения первоначальной системы вычесть первое уравнение, т. е. в ячейку B7 ввести формулу =B3-B2 и протянуть ее до ячейки E7.
Для того чтобы получить второе уравнение новой системы, нужно второе уравнение первоначальной системы сложить с первым уравнением, т. е. в ячейку B8 ввести формулу =B3+B4 и протянуть ее до ячейки E8.
Для того чтобы получить третье уравнение новой системы, нужно из третьего уравнения первоначальной системы вычесть первое уравнение, т. е. в ячейку B9 ввести формулу =B4-B2 и протянуть ее до ячейки E9.
Разделить каждое уравнение полученной системы на соответствующий диагональный коэффициент:
В ячейку B12 ввести формулу =B7/$B$7 и протянуть ее до ячейки E12.
В ячейку B13 ввести формулу =B8/$C$8 и протянуть ее до ячейки E13.
В ячейку B14 ввести формулу =B9/$D$9 и протянуть ее до ячейки E14.
В результате получаем следующее:
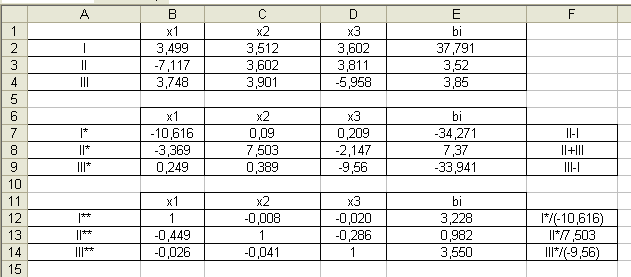
Последовательно из каждой строки выразить неизвестные x1, x2, x3:
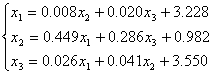
В Excel данную картину можно изобразить следующим образом:
Нужно определить метрику:
Найти q для метрики
:
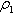- В ячейку B21 ввести q1.
- В ячейку В22 ввести формулу =ABS(C18)+ABS(C19).
- В ячейку В23 ввести формулу =ABS(D17)+ABS(D19).
- В ячейку В24 ввести формулу =ABS(E17)+ABS(E18).
Таким образом, максимальным из полученных значений является q1=0,449<1, т. е. подходит.
- В ячейку A22 ввести выражение q1=.
Найти q для метрики
:
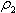- В ячейку D21 ввести q2.
- В ячейку D22 ввести формулу =ABS(D17)+ABS(E17).
- В ячейку D23 ввести формулу =ABS(C18)+ABS(E18).
- В ячейку D24 ввести формулу =ABS(C19)+ABS(D19).
Таким образом, максимальным из полученных значений является q2=0,735<1, т. е. подходит.
- В ячейку C23 ввести выражение q2=.
Найти q для метрики
:
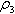- В ячейку F21 ввести q3.
- В ячейку F22 ввести формулу =D17^2+E17^2+C18^2+E18^2+C19^2+D19^2.
- В ячейку F23 ввести формулу =КОРЕНЬ(F22).
Таким образом, q3=0,533<1, т. е. подходит.
- В ячейку E23 ввести выражение q3=.
Проделанные вычисления представлены на рисунке:
Для дальнейших вычислений выбрать q минимальное, т. е. q=0,475, записать это значение в ячейку F26.
В ячейку G26 ввести текст а=.
В ячейку H26 ввести =0,001*(1-F26)/F26.
Заполнить диапазон ячеек B28:I28 следующим образом:
В ячейку B30 ввести формулу =$D$17*C29+$E$17*D29+$F$17.
В С30 ввести =$C$18*B29+$E$18*D29+$F$18.
В D30 ввести =$C$19*B29+$D$19*C29+$F$19.
В E30 ввести =ABS(B30-B29).
В F30 ввести =ABS(C30-C29).
В G30 ввести =ABS(D30-D29).
В H30 ввести =СУММ(E30:G30).
В I30 ввести =ЕСЛИ(H30<=$H$26;"ответ").
Выделить диапазон ячеек B30:I30 и методом протягивания заполнить нижние строки до получения слова "ответ" в одной из ячеек столбца I (диапазон ячеек B30:I35).
В конечном итоге получаем следующее:
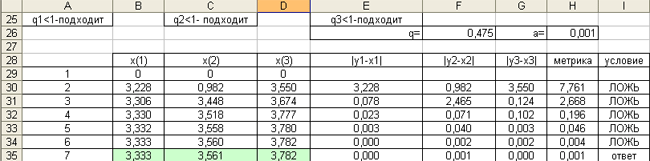
Ответ: x1=3.332, x2=3.561, x3=3.782.