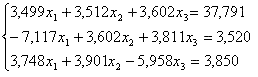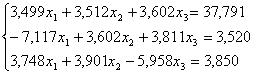- •1. Графический способ отделения корней
- •1 Способ
- •2 Способ
- •2. Аналитический способ отделения корней
- •1. Метод половинного деления
- •Метод хорд
- •3. Метод касательных (Ньютона)
- •4. Комбинированный метод хорд и касательных
- •1. Метод Гаусса
- •2. Матричный метод
- •3. Метод Крамера
- •4. Метод итераций
- •1. Формула трапеций
- •2. Формула Симпсона (парабол)
- •3. Формулы прямоугольников
- •1. Метод Монте-Карло
- •1. Метод наименьших квадратов
- •1. Интерполяционный многочлен Лагранжа
2. Матричный метод
Систему вида (12) можно представить в виде "Ax=b, где b=(b1,b2,b3,...,bn)T - вектор свободных членов и x=(x1,x2,x3,...,xn)T - вектор неизвестных с вещественными координатами, а A=(aij)ni,j=1 - вещественная n ×n - матрица коэффициентов данной системы"[3]. "Тогда, умножая обе части этого векторного уравнения слева на обратную матрицу A-1 , получаем x=A-1b (13)"[5].
На практике данный способ реализуется следующим образом:
|
Решить систему уравнений: |
|
методом Гаусса в: |
Mathcad;
Excel.
Для того чтобы решить данную систему уравнений в Excel, нужно выполнить следующие действия:
В ячейку A2 ввести текст «А=».
Ячейки B1:D3 заполнить значениями коэффициентов перед x1, x2, x3 каждого уравнения системы:
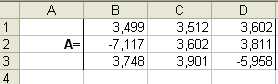
(т. о. сформировали матрицу системы).
В A6 ввести «b=», затем ячейки B5:B7 заполнить значениями свободных членов:
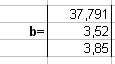
(т. о., сформировали вектор – столбец свободных членов).
В ячейку А10 ввести «A^(-1)=».
Выделить диапазон ячеек В9:D11, нажать с клавиатуры знак равенства (=), выбрать меню «Вставка» - «Функция» - «МОБР» (данная функция позволяет найти обратную функцию исходной матрицы).
В окне «Аргументы функции» задать массив B1:D3, нажать на клавиатуре Ctrl+Shift+Enter (т. о., нашли обратную матрицу системы).
В А14 набрать «x=».
Выделить диапазон ячеек B13:B15, нажать «=» с клавиатуры, выбрать функцию «МУМНОЖ», которая возвращает произведение матриц.
В окне «Аргументы функции» в поле массив1 ввести B9:D11 и в поле массив2 ввести B5:B7, нажать на клавиатуре Ctrl+Shift+Enter.
Таким образом, получаем следующее:

Ответ: x1=3.332888, x2=3.561042, x3=3.782022.
3. Метод Крамера
|
"В общем виде формулы Крамера выглядят (14): |
|
"[3] . |
Где det Ai - это определитель i-го порядка (i=1,2,...,n) матрицы A, а det A - определитель матрицы A.
Примечание: определитель i-го порядка отличается от определителя матрицы тем, что при составлении определителя используется столбец свободных членов.
На практике данный способ реализуется следующим образом:
|
Решить систему уравнений: |
|
методом Гаусса в: |
Mathcad
Для того чтобы решить данную систему уравнений в Excel, нужно выполнить следующие действия:
В ячейку A2 ввести: А=.
Ячейки B1:D3 заполнить значениями коэффициентов перед x1, x2, x3 каждого уравнения системы:
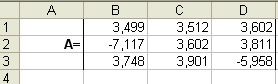
(т. о. сформировали матрицу системы).
В A6 ввести «b=», затем ячейки B5:B7 заполнить значениями свободных членов:
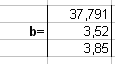
(т. о., сформировали вектор – столбец свободных членов).
В ячейку А9 ввести «|A|=».
В ячейку B9 ввести: =, меню «Вставка» - «Функция» - «МОПРЕД» (функция МОПРЕД возвращает определитель матрицы), массив: B1:D3.
Вычислить определители матриц, полученных заменой соответствующего столбца исходной матрицы столбцом свободных членов:
В ячейку A12 ввести «D1=» (условно обозначает матрицу первого порядка).
В ячейку B11 ввести формулу =B5 и протянуть ее до ячейки B13.
В ячейку С11 ввести формулу =С1 и протянуть ее до ячейки С13.
В ячейку D11 ввести формулу =D1 и протянуть ее до ячейки D13.
В ячейку F12 ввести «|D1|=» (условно обозначает определитель первого порядка).
В ячейку G12 ввести формулу =МОПРЕД(B11:D13).
В ячейку A16 ввести «D2=» (условно обозначает матрицу первого порядка).
В ячейку B15 ввести формулу =B1 и протянуть ее до ячейки B17.
В ячейку С15 ввести формулу =B5 и протянуть ее до ячейки С17.
В ячейку D15 ввести формулу =D1 и протянуть ее до ячейки D17.
В ячейку F16 ввести «|D2|=» (условно обозначает определитель первого порядка).
В ячейку G16 ввести формулу =МОПРЕД(B15:D17).
В ячейку A20 ввести «D3=» (условно обозначает матрицу первого порядка).
В ячейку B19 ввести формулу =B1 и протянуть ее до ячейки B21.
В ячейку С19 ввести формулу =С1 и протянуть ее до ячейки С21.
В ячейку D19 ввести формулу =B5 и протянуть ее до ячейки D21.
В ячейку F20 ввести «|D3|=» (условно обозначает определитель первого порядка).
В ячейку G20 ввести формулу =МОПРЕД(B19:D21).
Для того, чтобы вычислить x1, x2, x3, необходимо:
Заполнить ячейки A23:A25 соответственно: x1, x2, x3.
В ячейку B23 ввести формулу =G12/B9.
В ячейку B23 ввести формулу =G16/B9.
В ячейку B23 ввести формулу =G20/B9.
Таким образом, получаем следующее:
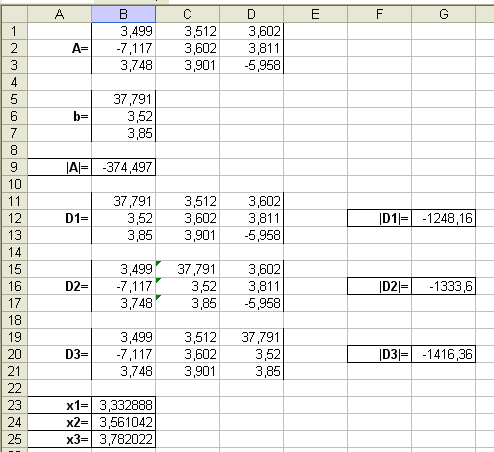
Ответ: x1=3.332888 , x2=3.561042 , x3=3.782022 .