2. Аналитический способ отделения корней

Аналитический способ отделения корней основан на следующей теореме:

Теорема 1.1.

1. " Если функция F(x), определяющая уравнениеF(x)=0, на концах отрезка[a;b]принимает значения разных знаков, т.е.F(a)*F(b)<0(3), то на этом отрезке содержится, по крайней мере, один корень уравнения"[4].

2. "Если функция F(x)строго монотонна, то корень на[a,b]единственный(F’(a)*F’(b)>0 (4)).

Для отделения корней аналитическим способом выбирается отрезок [A;B], на котором находятся все интересующие вычислителя корни уравнения. Причем на отрезке[A;B]функцияF(x)определена, непрерывна иF(a)*F(b)<0. Требуется указать все частичные отрезки[a;b], содержащие по одному корню.

Будем вычислять значение функции F(x), начиная с точкиx=A, двигаясь вправо с некоторым шагомh. ЕслиF(x)*F(x+h)<0, то на отрезке[x;x+h] существует корень:"[1]

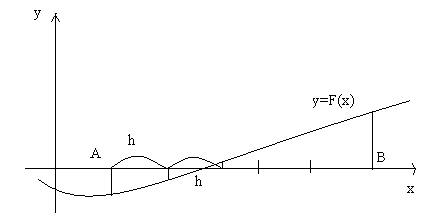
Если F(x_k)=0, x_k-точный корень.(5)

На практике данный способ реализуется следующим образом:например дана такая задача: на основании найденного отрезка изоляции (см.графический способ отделения корней):

1. доказать существование и единственность корня на полученном отрезке с помощью:

   1. Mathcad;

   2. Excel.

2. отделить корни уравнения cos(2x)+x-5=0аналитическим способом с шагом 1 на отрезке [-10;10], используя:

   1. Mathcad;

   2. Excel.

Рассмотрим полученный отрезок изоляции [5;6].

Для доказательства существования корня на отрезке изоляции необходимо выполнить следующие действия:

1. Запустить MS Excel.

2. Ввести в ячейки А1, В1 и С1 соответственно «x», «y=cos(2x)+x-5» и «ответ».

3. В А2 и А3 ввести граничные значения отрезка изоляции.

4. В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.

5. В С2 ввести формулу =ЕСЛИ(B2*B3<0;"корень существует";"корень не существует").

Таким образом, на отрезке изоляции корень существует:

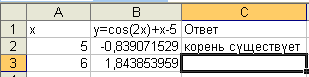
Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:

1. Продолжить работу в том же документе MS Excel.

2. Заполнить D1 и E1 соответственно: «y'=-sin(2x)*2+1» и «ответ» (причем выражение y'=-sin(2x)*2+1 – это производная первого порядка от функции y=cos(2x)+x-5).

3. Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

4. Ввести в E2 =ЕСЛИ(D2*D3>0;"корень на данном отрезке единственный";"Корень не единственный").

В результате получаем:

Таким образом доказано существование и единственность корня на отрезке изоляции.

Чтобы отделить корни уравнения аналитическим способом с помощью MS Excel, необходимо выполнить следующее:

1. Заполнить ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5», «h», «ответ».

2. В С2 ввести значение 1.

3. Ввести в А2 значение -10.

4. Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

5. В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

6. В С3 ввести формулу =ЕСЛИ(B2*B3<0;"Корень на отрезке существует";ЕСЛИ(B3=0;"точный корень";"-")) и методом протягивания заполнить диапазон ячеек С4:С22.

В результате получаем следующее:

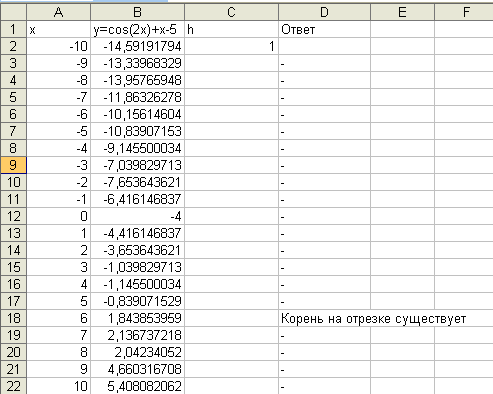
Ответ: Корень уравнения существует на отрезке [5;6].