1. Метод наименьших квадратов

"Пусть в результате эксперимента были получены некоторые значения, представленные в виде таблицы.

xi	yi
x0	y0
x1	y1
.	.
.	.
.	.
xn	yn

Расстояние между аргументами произвольное.

Нужно найти функцию g(x), приближенно описывающую функцию f(x).

Функция g(x) может выглядеть в виде линейной, квадратичной, степенной и так далее.

Рассмотрим линейную функцию.

В общем виде она выглядит: g=ax+b.

Запишем для данного случая систему:

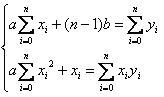
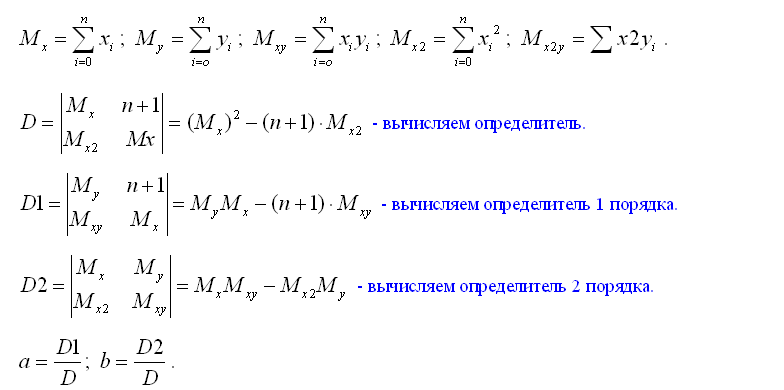
Рассмотрим квадратичную функцию.

В общем виде она выглядит: g=ax₂+bx+c

Запишем для данного случая систему:" [1]

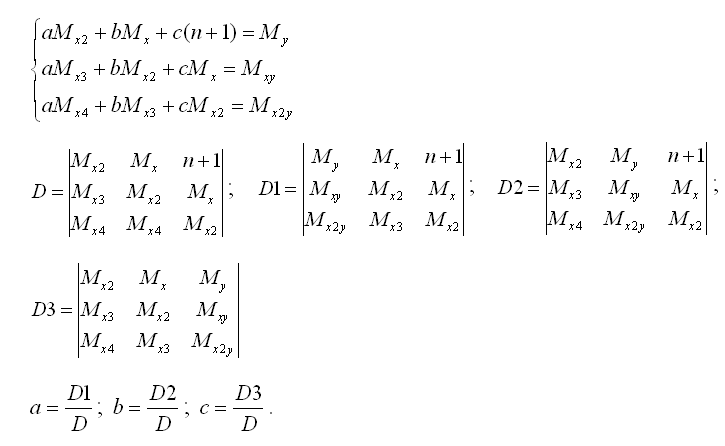
На практике данный способ реализуется следующим образом:Для данных, заданных в таблице установить линейную зависимость: g=ax+b.

xi	yi
2,5	21,55
3,1	23,65
5,9	33,45
6,3	34,85
7,8	40,1

с помощью:

Для того, чтобы установивить линейную зависимость для заданных табличных данных с помощью Excel, необходимо выполнить следующие действия:

1. В ячейки A1 и B1 ввести текст соответственно «xi» и «yi».

2. Заполнить диапазон ячеек A2:B6 значениями из таблицы:

   x0	y0
   x1	y1
   .	.
   .	.
   .	.
   xn	yn

3. В ячейку С1 ввести текст n=.

4. В ячейку D1 ввести число 4.

5. В ячейки C2:С5 ввести текст «Mx», «My», «Mxy», «Mx2» соответственно.

6. В ячейку D2 ввести формулу =СУММ(A2:A6).

7. В ячейку D3 ввести формулу =СУММ(B2:B6).

8. В ячейки A8, B8 ввести текст «x*y», «x^2» соответственно.

9. В ячейку A9 ввести формулу =A2*B2 и методом протягивания заполнить диапазон ячеек A10:A13.

10. В ячейку B9 ввести формулу =A2^2 и методом протягивания заполнить диапазон ячеек B10:B13.

11. В ячейку D4 ввести формулу =СУММ(A9:A13).

12. В ячейку D5 ввести формулу =СУММ(B9:B13).

13. В ячейки D8, D11, D14 текст «D=», «D1=», «D2=» соответственно.

14. В ячейку E8 и F9 ввести формулу = D2.

15. В ячейку E9 ввести формулу =D5.

16. В ячейку F8 ввести формулу =D1+1.

17. В ячейку H8 ввести текст «D=».

18. В ячейку I8 ввести формулу =МОПРЕД(E8:F9) (вычисляет определитель матрицы).

19. В ячейку E11 ввести формулу =D3.

20. В ячейку E12 ввести формулу =D4.

21. В ячейку F11 ввести формулу =D1+1.

22. В ячейку F12 ввести формулу =D2.

23. В ячейку H11 ввести текст «D1=».

24. В ячейку I11 ввести формулу =МОПРЕД(E11:F12) (вычисляет определитель матрицы).

25. В ячейку E14 ввести формулу =D2.

26. В ячейку E15 ввести формулу =D5.

27. В ячейку F14 ввести формулу =D3.

28. В ячейку F15 ввести формулу =D4.

29. В ячейку H14 ввести текст «D2=».

30. В ячейку I14 ввести формулу =МОПРЕД(E14:F15) (вычисляет определитель матрицы).

31. В ячейки A16 и A17 ввести текст «a=», «b=» соответственно.

32. В ячейку B16 ввести формулу =I11/I8.

33. В ячейку B17 ввести формулу =I14/I8.

В итоге получаем следующее:

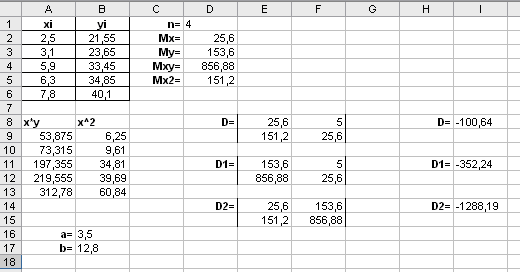
Ответ: g=3,5x+12,8.

1. Интерполяционный многочлен Лагранжа

"Пусть некоторая функция y=f(x) задана таблично:

i	xi	yi
0	x0	y0
1	x1	y1
.	.	.
.	.	.
.	.	.
n	xn	yn

Где x₀, x₁,..., x_n- узлы интерполяции. Причем, расстояние между узлами интерполяции произвольное.

В интерполировании находят значение функции в заданной точке x_k, принадлежащей отрезку[x₀;x_n], но x_kне совпадает ни с одним узлом интерполяции (x_kне равно x₀, x₁,...,x_n.)

Интерполяционную функцию подбирают из определенного класса функций. Часто такую функцию находят в виде интерполяционного многочлена F_n(x).

В качестве интерполяционного многочлена будем рассматривать интерполяционный многочлен Лагранжа L_n(x).

Многочлен Лагранжа строят следующим образом(24):

L_n(x)=l₀(x)+l₁(x)+l₂(x)+...+l_n(x), гдеl_i(x)вычисляется по следующей формуле(25):

Следовательно, интерполяционный многочлен Лагранжа для неравно отстающих узлов выглядит(26)[5]:

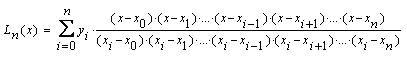
На практике данный способ реализуется следующим образом:используя формулу Лагранжа, найти приближенное значение функции:

i	xi	f(xi)
0	-1	-1,35078
1	-0,7	-0,14846
2	1,3	3,50988
3	2,5	16,13892
4	5,6	177,07487

в точке t=2,005 с помощью:

1. Mathcad;

2. Excel.

Для того, чтобы найти приближенное значение функции в точке t=2,005 с помощью Excel, необходимо выполнить следующие действия:

1. Заполнить нижеприведенные ячейки:

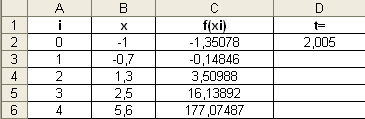
2. Ввести в ячейку A9 текст n=4.

3. Заполнить нижеприведенные ячейки:

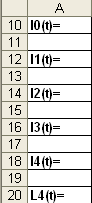
4. Ввести в ячейку B10 формулу =(C2*(D2-B3)*(D2-B4)*(D2-B5)*(D2-B6))/((B2-B3)*(B2-B4)*(B2-B5)*(B2-B6)).

5. Ввести в ячейку B12 формулу =(C3*(D2-B2)*(D2-B4)*(D2-B5)*(D2-B6))/((B3-B2)*(B3-B4)*(B3-B5)*(B3-B6)).

6. Ввести в ячейку B14 формулу =(C4*(D2-B2)*(D2-B3)*(D2-B5)*(D2-B6))/((B4-B2)*(B4-B3)*(B4-B5)*(B4-B6)).

7. Ввести в ячейку B16 формулу =(C5*(D2-B2)*(D2-B3)*(D2-B4)*(D2-B6))/((B5-B2)*(B5-B3)*(B5-B4)*(B5-B6)).

8. Ввести в ячейку B18 формулу =(C6*(D2-B2)*(D2-B3)*(D2-B5)*(D2-B4))/((B6-B2)*(B6-B3)*(B6-B4)*(B6-B5)).

9. Ввести в ячейку B20 формулу =B10+B12+B14+B16+B18.

В итоге получаем следующее:

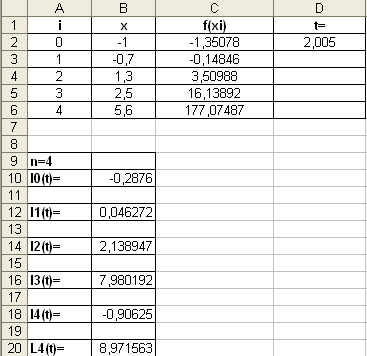
Ответ: приближенное значение функции в точке t=2,005 равно 8,971563.