14 Показникова і логарифмічна функції дійсних чисел.

Озн. Ф-ція виду , де – називається показниковою.

Озн. Ф-ція виду , деназивається показниковою.

1. Область визначення 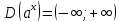. Якщо   . За означенням . За означенням . Якщо , .Якщо - ірраціональне число

2. Множина значень ;

3. ;

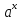4. –неперервна на R;

(зобраз графіки функції)

Озн. Нех ф-ція – бієктивно відображає. Ф-ція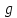 – називається оберненою до на , якщо кожному, ставиться у відповідність такий, для якого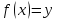, тоді.

Із означення ми отримуємо, що фунція – є оберненою до.

Т1.: « Якщо ф-ція – монотонна і неперервна на відрізку, то на відрізку з кінцямиіснує обернена ф-ція, яка неперервана і має характер монотонності, як ф-ціяна проміжку з кінцями»

Т2.: « Якщо ф-ція – монотонна і неперервна на інтервалі, і якщо,, то існує обернена ф-ція, яка неперервана і має характер монотонності, як ф-ціяна інтервалі з кінцями».Дов.

Має місце наступна лема: « Нехай ф-ція– строго зростає (спадає) на деякій множиніі нехай – множина її значень. Тоді обернена функція – є однозначно строго зростаючою (спадною) функцією на множині ».

Нехай для визначеності функція – строго зростає в інтервалі.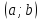

Із леми маємо, що функція – однозначна і строго зростає в інтервалі . Неперервністьфункції випливає із Т1, тому, що .

Покажемо, що в цьому випадку множина значень ф-ції передставляє собою інтервал . Дійсно, згідно теореми про границях моноттоних функцій маємо , виконується нерівність . Більше того, виконуються ще дві нерівності:. Справді, якщо, наприклад, існувало б таке, щоі( це можливо тоді, коли нижня грань - скінченна), то при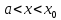виконувалася б нерівність, але оскільки нижня грань множини не більша від будь-якого елементу множини, то нерівність (1) – суперечлива , щоі . Аналогічно можна показати, що .

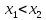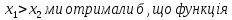
З іншого боку, ,, тому,, що , що задовільняють умову  (у випадку, коли ), і оскільки, то за теоремою Больцано-Коші (про проміжні значення неперервних функцій),, що. Тим самим ми показали, що множиною значень функції – є і множиною визначення функції – є інтервал. Теорема для строго спадної функції доводиться аналогічно.Довед. Має місце узагальнена теорема: « Якщо ф-ція – монотонна і неперервна на проміжку, то на проміжку з кінцямиіснує обернена ф-ція, яка неперервана і має характер монотонності, як ф-ціяна проміжку з кінцями»

Оскільки показник 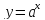– функція монотонна і неперервна наR, то на множині додатніх чисел обернена ф-ція, яка на цій множині неперервна і монотонна, ця функція називається логарифмічною функцією. Із означ: , при. З іншого боку маємо:- відома з школи основна логарифмічна тотожність. (побуд графіки прямої та оберн ф-ції).

15 Розвиток поняття степеня з дійсним показником. Властивості степеня. Загальна степенева функція дійсної змінної (озн, вл, графік).

Див. п14.

Вл степеня:

(степені з довільним показником розглядаються тільки для додатніх ознов: )

1) ; 2); 3); 4); 5).

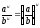Степенева ф-ція (де показник – натуральний, з цілим від’ємним показником, з додатнім раціональним, з раціональним показником, з ірраціональним показником).

, тобто загальна степенева функція – є композицією логарифмічної та показникової. – монотонно зростає і неперервна, показникова – монотонна і неперервна на проміжку. Якщо– то загальна степенева функція – зростає, якщо Якщо– спадає.