
- •1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
- •2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
- •3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
- •4. Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
- •5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
- •6. Похідна функції дійсної змінної та її основні властивості. Диференційовність і диференціал функції
- •8. Основні теореми диференціального числення. Теореми Ролля, Лагранжа й Коші. Формула Тейлора.
- •9. Застосування диференціального числення до дослідження властивостей функції. Умови сталості і монотонності функції на проміжку. Екстремуми функції.
- •Достатні умови існування екстремуму функції. Теорема. Нехай критична точка функції ,неперервна в точціі має похіднув усіх точках околуза виключенням, можливо самої точки. Тоді
- •10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
- •11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
- •12. Інтеграла Рімана для функції однієї змінної. Основні властивості.
- •13 Критерій інтегровності. Основні класи інтегровних за Ріманом функцій.
- •14 Показникова і логарифмічна функції дійсних чисел.
- •15 Розвиток поняття степеня з дійсним показником. Властивості степеня. Загальна степенева функція дійсної змінної (озн, вл, графік).
- •16 Тригонометричні та обернені тригонометричні функції дійсної зміної (означення неперервність, властивості, графік).
- •18. N-вимірний евклідів простір як узагальнення просторів
- •19 Числові ряди. Геометрична прогресія та гармонійний ряд. Властивості збіжних рядів.
- •20 Додатні ряди, основні ознаки збіжності додатніх рядів. Ряди з довільними членами. Абсолютно і умовно збіжні ряди.
11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
Функція
 називається первісною для функції
називається первісною для функції ,
на деякому проміжкуХ,
якщо для усіх значень х
Х
виконується рівність
,
на деякому проміжкуХ,
якщо для усіх значень х
Х
виконується рівність
 =
= .
Якщо
.
Якщо

первісна для функції
первісна для функції
 ,
то й функція
,
то й функція ,
деС
довільна стала, також є первісною для
функції
,
деС
довільна стала, також є первісною для
функції
 ,
оскільки(
,
оскільки( )′
=
)′
=
 +
С ′=
+
С ′=
 + 0 =
+ 0 = .
.
Нехай первісною
функції
 на проміжкуХ,
крім функції
на проміжкуХ,
крім функції
 ,
є функція
,
є функція ,
тобто
,
тобто =
= .
Розглянемо різницю
.
Розглянемо різницю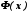
 .
Обчислимо похідну цієї різниці.
(
.
Обчислимо похідну цієї різниці.
(
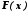 )′
=
)′
=
 =
=
 = 0.
Отже, згідно
з теоремою Лагранжа
= 0.
Отже, згідно
з теоремою Лагранжа

 = С.
Звідси маємо:
= С.
Звідси маємо:
 =
= +С.
множина первісних функції
+С.
множина первісних функції
 на проміжкуХ,
вичерпується функціями виду
на проміжкуХ,
вичерпується функціями виду +С,
де
+С,
де

одна із первісних функції
одна із первісних функції
 .
.
Означення.
Сукупність усіх первісних функції
 на проміжкуХ
називається невизначеним інтегралом
функції
на проміжкуХ
називається невизначеним інтегралом
функції
 на цьому проміжку і позначається
на цьому проміжку і позначається .
Невизначений
інтеграл інакше називають інтегралом
Ньютона
Лейбніца.
Якщо
.
Невизначений
інтеграл інакше називають інтегралом
Ньютона
Лейбніца.
Якщо

одна з первісних функції
одна з первісних функції
 ,
то за означенням
,
то за означенням
 =
=
 +С.
Знак
+С.
Знак
 називається
знаком невизначеного інтеграла,
називається
знаком невизначеного інтеграла,
підінтегральною функцією, а
підінтегральною функцією, а
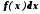
підінтегральним виразом.
Операцію
знаходження невизначеного інтеграла
від функції називають інтегруванням
цієї функції.
підінтегральним виразом.
Операцію
знаходження невизначеного інтеграла
від функції називають інтегруванням
цієї функції.
Основні властивості
невизначеного інтеграла:
1. Похідна
від невизначеного інтеграла дорівнює
підінтегральній функції. (
( )′
=
)′
=
 +
С ′=
+
С ′=
 .
2. Диференціал
від невизначеного інтеграла дорівнює
підінтегральному виразу
.
2. Диференціал
від невизначеного інтеграла дорівнює
підінтегральному виразу
 d(
d( )
= d
)
= d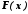 =
=
 d(x).
3. Н.І.
від
диференціала деякої функції дорівнює
сумі цієї функції і довільної постійної
d(x).
3. Н.І.
від
диференціала деякої функції дорівнює
сумі цієї функції і довільної постійної
 =
=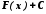 .
4. Сталий
множник можна виносити за знак інтеграла,
тобто, якщо k
= const
0, то
.
4. Сталий
множник можна виносити за знак інтеграла,
тобто, якщо k
= const
0, то (Для
доведення цієї властивості досить
показати, що права чстина рівності є
первісною підінтегральної функції
(Для
доведення цієї властивості досить
показати, що права чстина рівності є
первісною підінтегральної функції
 ). 5.
Невизначений інтеграл від суми (різниці)
функцій дорівнює сумі (різниці)
невизначених інтегралів від кожної
функції, тобто
). 5.
Невизначений інтеграл від суми (різниці)
функцій дорівнює сумі (різниці)
невизначених інтегралів від кожної
функції, тобто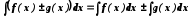 .
Доведення.
.
Доведення. .
.
Таблиця основних
інтегралів Безпосередньо
із означення визначеного інтеграла
випливають наступні формули, котрі
утворюють таблицю основних інтегралів:
1. ,
2.
,
2.
 ,
3.
,
3.
 ,
4.
,
4.
 5.
5.
 ,
6.
,
6. ,
7.
,
7. ,
8.
,
8.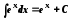 ,
9.
,
9. ,
10.
,
10. ,
11.
,
11. ,
12.
,
12. ,
13.
,
13. ,
14.
,
14. .
.
СПОСОБИ
ІНТЕГРУВАННЯ: Безпосереднє
інтегрування Обчислення
інтегралів за допомогою безпосереднього
використання таблиці основних інтегралів
та їх властивостей називається
безпосереднім інтегруванням. Метод
підстановки
В основі
методу підстановки (методу заміни
змінної) лежить формула диференціювання
складеної функції. Якщо F
′( x)
= f(x),
х(a,
b),
то для довільної диференційованої на
проміжку (,
) функції
x=
(t),
де (t)
(a,
b),
якщо
t
(,
) маємо:
(F((t)))′
= F
′( x)
′(t)
= f(x)
′(t)
= f((t))
′(t).
Таким
чином,
 ,
тобто
,
тобто .
Інтегрування
частинами
Нехай
функції
.
Інтегрування
частинами
Нехай
функції
 і
і визначені й диференційовані на деякому
проміжкуХ.
Тоді
визначені й диференційовані на деякому
проміжкуХ.
Тоді
 .
Звідси маємо
.
Звідси маємо
 .
Припустимо, що інтеграл
.
Припустимо, що інтеграл існує. Тоді
існує. Тоді .
Оскільки
.
Оскільки ,
то
,
то (1).
Довільну сталуС
включає в себе інтеграл
(1).
Довільну сталуС
включає в себе інтеграл
 .
Формула (1) називається формулою
інтегрування частинами.За
цією формулою обчислюються , зокрема
інтеграли виду
1)
.
Формула (1) називається формулою
інтегрування частинами.За
цією формулою обчислюються , зокрема
інтеграли виду
1)
 ,
,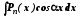 ,
, ,
де
,
де

многочлен n-ного
степеня відносно х,
многочлен n-ного
степеня відносно х,
 .
Тут слід прийняти
.
Тут слід прийняти .
.
