6. Похідна функції дійсної змінної та її основні властивості. Диференційовність і диференціал функції

Нехай в деякому проміжку 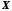визначена функція. Виберемо довільну точкуі надамо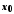приростутакого, що. Зазначимо, що може бути як додатним, так і від'ємним. При цьому функція одержить приріст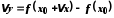. Нехай в точцііснує границя.

Похідною функції в точціназивається границя відношення приросту функції до приросту аргументу за умови, що приріст аргументу прямує до нуля. Похідну функції в точціпозначають так:або. Отже, за означенням. Якщо функція має похідну в кожній точці, то похідна є функцією віді в цьому випадку позначається так:або.

Односторонні похідні Використовуючи означення правої і лівої границі, введемо поняття правої і лівої похідної функції в точці.Правою (лівою) похідною функції в точціназивається права (ліва) границя відношенняпри(за умови, що ця границя існує). Права похідна позначається так: , а ліва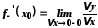. Якщо функціяв точцімає похідну, то вона має як праву, так і ліву похідну і ці похідні рівні між собою.Проте не в кожній точці , у якій існують права і ліва похідні, існує похідна функції. Так, наприклад, функціяв точцімає праву похідну і ліву 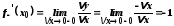, але похідної в точціфункціяне має, оскільки.

Диференційовність функції Функція 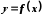називається диференційованою в точці, якщо її приріст у цій точці можна подати у вигляді, (1) де- деяке число, не залежне від, а- нескінчено мала функція при, тобто. Зв'язок між диференційованістю функціїв точціі існуванням похідної даної функції в цій точці установлюється наступною теоремою. Теорема. Для того, щоб функція функції була диференційована в точці, необхідно і достатньо, щоб вона мала в цій точці скінчену похідну. Доведення. Необхідність. Нехай функція 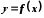диференційована в точці, тобто її приріст можна подати у вигляді (1). Тоді. Звідси випливає, що в точці існує похідна. Достатність. Нехай функція має в точці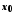похідну. За означенням похідної маємо. За властивістю границіє нескінченно малою функцією при. Отже,, тобто, де деяке число, а .

Зауваження. Вираз 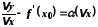не визначений при, а отже, за цієї умови не визначений вираз (1). Щоб позбутися цієї невизначеності достатньо покласти.Зв'язок між диференційованістю і неперервністю функції розкривається в наступній теоремі.

Теорема . Якщо функція диференційована в точці, то вона в цій точці неперервна.

Доведення. Так як функція диференційована в точці, то її приріст в цій точці можна подати у вигляді.Тоді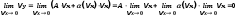. Отже, в точці , де функціядиференційована, нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції, а це означає, що в точціфункціянеперервна.

Наслідок. Якщо функція в кожній точці деякого проміжку має скінчену похідну, то на цьому проміжку вона неперервна. Зауваження. Неперервність функції в даній точці не є достатньою умовою її диференційованості. Наприклад, функція неперервна в точці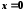, але в цій точці, як вона не диференційована.

Диференціал функції. Нехай функція диференційована в точці. Тоді її приріст у цій точці можна подати у вигляді , де при. Отже, доданок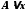є головною частиною приросту функції, яка лінійно залежить від. Диференціалом функції в точці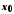називається головна частина приросту функції в цій точці, яка лінійно залежить від. Диференціал функції позначається так: . Враховуючи, що, маємо. Диференціалом незалежної змінноїназивається її приріст:. Отже,. Із останньої формули випливає, що похіднуможна обчислити як відношення диференціалів:. Якщо функціїдиференційовані, то мають місце наступні формули:,,,. 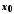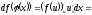Нехай тепер маємо складену функцію, дедиференційовані функції в точкахі.Тоді Таким чином, .Якщо функція складена, то форма диференціалу не змінює свого виду. Цю властивість називають інваріантністю форми диференціалу.

7. Частинні похідні функції кількох змінних. Диференційовність та диференціал функції кількох змінних. Необхідна та достатня умови диференційовності.