
- •1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
- •2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
- •3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
- •4. Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
- •5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
- •6. Похідна функції дійсної змінної та її основні властивості. Диференційовність і диференціал функції
- •8. Основні теореми диференціального числення. Теореми Ролля, Лагранжа й Коші. Формула Тейлора.
- •9. Застосування диференціального числення до дослідження властивостей функції. Умови сталості і монотонності функції на проміжку. Екстремуми функції.
- •Достатні умови існування екстремуму функції. Теорема. Нехай критична точка функції ,неперервна в точціі має похіднув усіх точках околуза виключенням, можливо самої точки. Тоді
- •10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
- •11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
- •12. Інтеграла Рімана для функції однієї змінної. Основні властивості.
- •13 Критерій інтегровності. Основні класи інтегровних за Ріманом функцій.
- •14 Показникова і логарифмічна функції дійсних чисел.
- •15 Розвиток поняття степеня з дійсним показником. Властивості степеня. Загальна степенева функція дійсної змінної (озн, вл, графік).
- •16 Тригонометричні та обернені тригонометричні функції дійсної зміної (означення неперервність, властивості, графік).
- •18. N-вимірний евклідів простір як узагальнення просторів
- •19 Числові ряди. Геометрична прогресія та гармонійний ряд. Властивості збіжних рядів.
- •20 Додатні ряди, основні ознаки збіжності додатніх рядів. Ряди з довільними членами. Абсолютно і умовно збіжні ряди.
4. Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
Нехай функція
 визначена в деякому околі точки
визначена в деякому околі точки![]() .
Функція
.
Функція називається неперервною в точці
називається неперервною в точці![]() ,
якщо
,
якщо .
.
(Гейне) Функція
 називається неперервною в точці
називається неперервною в точці![]() ,
якщо для будь-якої послідовності
,
якщо для будь-якої послідовності відповідна послідовність
відповідна послідовність значень збігається до
значень збігається до .
.
(Коші)
Функція
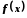 називається неперервною в точці
називається неперервною в точці![]() ,
якщо для довільного числа
,
якщо для довільного числа існує число
існує число таке, що для всіх
таке, що для всіх ,
які задовольняють умову
,
які задовольняють умову ,
виконується нерівність
,
виконується нерівність .Наведені
означення рівносильні.
.Наведені
означення рівносильні.
Функція
 називається неперервною в точці
називається неперервною в точці![]() справа (зліва), якщо
справа (зліва), якщо .
Покажемо,
що неперервна функція характеризується
тим, що нескінченно малому приростові
аргументу
.
Покажемо,
що неперервна функція характеризується
тим, що нескінченно малому приростові
аргументу
 відповідає нескінченно малий приріст
функції
відповідає нескінченно малий приріст
функції .
Дійсно, умову
.
Дійсно, умову можна записати як
можна записати як .
Тоді
.
Тоді .
наступне означення неперервності
функції в точці:
Функція
.
наступне означення неперервності
функції в точці:
Функція
 називається неперервною в точці
називається неперервною в точці![]() ,
якщо нескінченно малому приростові
аргументу в цій точці відповідає
нескінченно малий приріст функції
(локальна або місцева властивість).
Якщо функція
,
якщо нескінченно малому приростові
аргументу в цій точці відповідає
нескінченно малий приріст функції
(локальна або місцева властивість).
Якщо функція
 неперервна
в кожній точці інтервалу
неперервна
в кожній точці інтервалу
 ,
то говорять, що вона неперервна на
інтервалі
,
то говорять, що вона неперервна на
інтервалі![]() .
Якщо при цьому в точці
.
Якщо при цьому в точці функція неперервна справа, а в точці
функція неперервна справа, а в точці –
неперервна зліва, то говорять, що функція
–
неперервна зліва, то говорять, що функція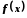 неперервна
на відрізку
неперервна
на відрізку
 .
Термін неперервної кривої походить із
поняття неперервної функції. Графіком
неперервної на
.
Термін неперервної кривої походить із
поняття неперервної функції. Графіком
неперервної на
 функції є неперервна крива ("суцільна
крива").
функції є неперервна крива ("суцільна
крива").
Приклади: показникова, функція, що задана многочленом, sin, cos.
Властивості:
Якщо функції
 неперервні в точці
неперервні в точці![]() ,
то функції
,
то функції у точці
у точці![]() також неперервні (доведення цієї теореми
безпосередньо випливає з означення
неперервності функції в точці та
властивостей границь); Якщо функція
також неперервні (доведення цієї теореми
безпосередньо випливає з означення
неперервності функції в точці та
властивостей границь); Якщо функція неперервна в точці
неперервна в точці![]() ,
а функція
,
а функція неперервна в точці
неперервна в точці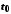 ,
причому
,
причому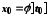 ,
то складена функція
,
то складена функція неперервна, як функція від
неперервна, як функція від ,
у точці
,
у точці .
.
Доведемо
останню властивість, яку часто записують
у вигляді теореми про неперервність
складеної функції в точці. Нехай
задано довільне число
 .
Тоді за неперервністю функції
.
Тоді за неперервністю функції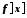 у точці
у точці![]() знайдеться число
знайдеться число таке, що
таке, що для всіх
для всіх ,
які задовольняють умову
,
які задовольняють умову .
.
Для числа
 за неперервністю функції
за неперервністю функції у точці
у точці знайдеться число
знайдеться число таке, що
таке, що для всіх
для всіх ,
які задовольняють умову
,
які задовольняють умову .
.
Отже, для довільного
числа
 знайдеться число
знайдеться число таке, що з умови
таке, що з умови випливає нерівність
випливає нерівність ,
а це означає, що функція
,
а це означає, що функція неперервна в точці
неперервна в точці .
Довед.
.
Довед.
Важливим
є те, що з
означення неперервності функції
 у точці
у точці випливає
випливає
 .
Наведемо
приклади деяких важливих границь,
обчислення яких спирається на неперервність
елементарних функцій.
.
Наведемо
приклади деяких важливих границь,
обчислення яких спирається на неперервність
елементарних функцій.
 .
Доведення.
.
Доведення. .
.
5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
Див
п.4(оглядово). Якщо
функція
 неперервна
в кожній точці інтервалу
неперервна
в кожній точці інтервалу
 ,
то говорять, що вона неперервна на
інтервалі
,
то говорять, що вона неперервна на
інтервалі![]() .
Якщо при цьому в точці
.
Якщо при цьому в точці функція неперервна справа, а в точці
функція неперервна справа, а в точці –
неперервна зліва, то говорять, що функція
–
неперервна зліва, то говорять, що функція неперервна
на відрізку
неперервна
на відрізку
 .
.
Основні властивості
неперервних функцій.
Перша
теорема Больцано-Коші (теорема про
обернення функції в нуль).
Нехай функція
 неперервна на відрізку
неперервна на відрізку і на його кінцях значення функції мають
різні знаки. Тоді існує точка
і на його кінцях значення функції мають
різні знаки. Тоді існує точка така, що
така, що .
.
Доведення.
Нехай для визначеності
 .
Розділимо відрізок
.
Розділимо відрізок навпіл. Якщо
навпіл. Якщо ,
то теорема доведена. Якщо
,
то теорема доведена. Якщо ,
то виберемо ту половину відрізка
,
то виберемо ту половину відрізка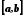 ,
на кінцях якої функція
,
на кінцях якої функція має значення різних знаків, і позначимо
її
має значення різних знаків, і позначимо
її .
Розділимо відрізок
.
Розділимо відрізок навпіл. Якщо
навпіл. Якщо ,
то теорема доведена, в іншому випадку
виберемо ту половину відрізка
,
то теорема доведена, в іншому випадку
виберемо ту половину відрізка ,
на кінцях якої функція
,
на кінцях якої функція має значення різних знаків, та позначимо
її
має значення різних знаків, та позначимо
її .
Якщо цей процес продовжувати необмежено,
то або на якомусь
.
Якщо цей процес продовжувати необмежено,
то або на якомусь -ому
кроці значення функції в середині
відрізка
-ому
кроці значення функції в середині
відрізка буде рівним нулю і тоді теорема доведена,
або одержимо послідовність укладених
відрізків
буде рівним нулю і тоді теорема доведена,
або одержимо послідовність укладених
відрізків
 таких, що
таких, що
 при
при і на кінцях кожного з відрізків
і на кінцях кожного з відрізків функція
функція має значення різних знаків,
має значення різних знаків,![]() .
.
За теоремою про
вкладені відрізки існує точка
 ,
яка належить кожному із відрізків
,
яка належить кожному із відрізків і
і
 .
Ураховуючи неперервність функції
.
Ураховуючи неперервність функції (зокрема в точці
(зокрема в точці ),
маємо
),
маємо .
Звідси
одержуємо
.
Звідси
одержуємо
 .
.
Друга теорема
Больцано-Коші (теорема про проміжне
значення).
Нехай функція
 неперервна на відрізку
неперервна на відрізку і на кінцях цього відрізка приймає
значення
і на кінцях цього відрізка приймає
значення де
де .
Тоді для будь-якого числа
.
Тоді для будь-якого числа існує точка
існує точка така, що
така, що .
.
Доведення.
Нехай для визначеності
 .
Розглянемо допоміжну функцію
.
Розглянемо допоміжну функцію
 .
Ця функція неперервна на відрізку
.
Ця функція неперервна на відрізку
 і
і
 ,
,
 .
За першою
теоремою Больцано-Коші існує точка
.
За першою
теоремою Больцано-Коші існує точка
 така, що
така, що .
Але
.
Але .
Отже,
.
Отже, ,
тобто
,
тобто .
.
Перша
теорема Вейєрштрасса.
Якщо функція
 неперервна на відрізку
неперервна на відрізку ,
то вона обмежена на цьому відрізку.
,
то вона обмежена на цьому відрізку.
Доведення.
Нехай функція
 неперервна на відрізку
неперервна на відрізку .
Припустимо, що вона на відрізку
.
Припустимо, що вона на відрізку не обмежена. Поділимо відрізок
не обмежена. Поділимо відрізок пополам і виберемо ту його частину, де
функція
пополам і виберемо ту його частину, де
функція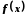 не обмежена. Позначимо її
не обмежена. Позначимо її .
Відрізок
.
Відрізок також поділимо пополам і виберемо ту
його частину, де функція
також поділимо пополам і виберемо ту
його частину, де функція не обмежена. Позначимо вибрану половину
не обмежена. Позначимо вибрану половину .
Продовжуючи необмежено цей процес,
одержимо послідовність укладених
відрізків
.
Продовжуючи необмежено цей процес,
одержимо послідовність укладених
відрізків
 таких, що
таких, що
 при
при .
За теоремою про вкладені відрізки існує
точка
.
За теоремою про вкладені відрізки існує
точка ,
яка належить кожному із них і
,
яка належить кожному із них і .
За означенням границі послідовності
для будь-якого числа
.
За означенням границі послідовності
для будь-якого числа >0
існує такий номер
>0
існує такий номер ,
що при
,
що при з іншого боку, існує такий номер
з іншого боку, існує такий номер ,
що при
,
що при .
Нехай
.
Нехай .
Тоді при
.
Тоді при виконуються нерівності:
виконуються нерівності: , тобто всі відрізки
, тобто всі відрізки ,
де
,
де попадають в інтервал
попадають в інтервал .
Таким чином, функція
.
Таким чином, функція не обмежена в деякому
не обмежена в деякому -околі
точки
-околі
точки .
Але це неможливо, оскільки функція
.
Але це неможливо, оскільки функція неперервна на відрізку
неперервна на відрізку ,
а значить, неперервна і в точці
,
а значить, неперервна і в точці ,
тобто в точці
,
тобто в точці існує скінченна границя функції
існує скінченна границя функції ,
а тому в околі цієї точки вона обмежена.
,
а тому в околі цієї точки вона обмежена.
Друга
теорема Вейєрштрасса.
Якщо функція
 неперервна на відрізку
неперервна на відрізку ,
то вона досягає на цьому відрізку своїх
точних меж, тобто існують такі точки
,
то вона досягає на цьому відрізку своїх
точних меж, тобто існують такі точки ,
що
,
що
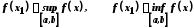 .
Доведення.
Нехай функція
.
Доведення.
Нехай функція
 неперервна на відрізку
неперервна на відрізку .
За першою теоремою Вейєрштрасса функція
.
За першою теоремою Вейєрштрасса функція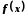 на відрізку
на відрізку обмежена. Отже, вона має точну верхню
межу
обмежена. Отже, вона має точну верхню
межу і точну нижню межу
і точну нижню межу .
Покажемо, що існує точка
.
Покажемо, що існує точка така, що
така, що .
Припустимо, що в жодній точці відрізка
.
Припустимо, що в жодній точці відрізка функція
функція не приймає значення, рівного
не приймає значення, рівного ,
тобто для всіх точок
,
тобто для всіх точок .
Складемо допоміжну функцію
.
Складемо допоміжну функцію .
Ця функція на відрізку
.
Ця функція на відрізку неперервна, а тому обмежена. Отже, існує
число
неперервна, а тому обмежена. Отже, існує
число таке, що для всіх
таке, що для всіх
 .
Із цієї
нерівності маємо:
.
Із цієї
нерівності маємо:
 .
Таким чином,
.
Таким чином, – верхня межа функції
– верхня межа функції на відрізку
на відрізку .
Але це суперечить тому, що число
.
Але це суперечить тому, що число
точна верхня межа цієї функції на
відрізку
точна верхня межа цієї функції на
відрізку
 .
Звідси випливає, що зроблене припущення
неправильне, тобто існує точка
.
Звідси випливає, що зроблене припущення
неправильне, тобто існує точка така, що
така, що .
Друга
частина теореми доводиться аналогічно.
.
Друга
частина теореми доводиться аналогічно.
