
- •1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
- •2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
- •3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
- •4. Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
- •5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
- •6. Похідна функції дійсної змінної та її основні властивості. Диференційовність і диференціал функції
- •8. Основні теореми диференціального числення. Теореми Ролля, Лагранжа й Коші. Формула Тейлора.
- •9. Застосування диференціального числення до дослідження властивостей функції. Умови сталості і монотонності функції на проміжку. Екстремуми функції.
- •Достатні умови існування екстремуму функції. Теорема. Нехай критична точка функції ,неперервна в точціі має похіднув усіх точках околуза виключенням, можливо самої точки. Тоді
- •10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
- •11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
- •12. Інтеграла Рімана для функції однієї змінної. Основні властивості.
- •13 Критерій інтегровності. Основні класи інтегровних за Ріманом функцій.
- •14 Показникова і логарифмічна функції дійсних чисел.
- •15 Розвиток поняття степеня з дійсним показником. Властивості степеня. Загальна степенева функція дійсної змінної (озн, вл, графік).
- •16 Тригонометричні та обернені тригонометричні функції дійсної зміної (означення неперервність, властивості, графік).
- •18. N-вимірний евклідів простір як узагальнення просторів
- •19 Числові ряди. Геометрична прогресія та гармонійний ряд. Властивості збіжних рядів.
- •20 Додатні ряди, основні ознаки збіжності додатніх рядів. Ряди з довільними членами. Абсолютно і умовно збіжні ряди.
3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
Нехай задано дві непусті множини Х та У. Якщо кожному значенні змінної х є Х ставиться у відповідність за деяким законом єдине значення у є У, то кажуть що на множині Х задана функція y=f(x). Множина X називається областю визначення функції позначається D(f). Множина У називається областю значень функцій позначається Е(f). При цьому х називається незалежною змінною або аргументом, у – залежною змінною.
Означення границі
функції за Гейне.
Число
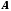 називається границею функції
називається границею функції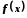 у точці
у точці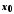 (
або при
(
або при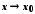 ),
якщо для будь-якої збіжної до
),
якщо для будь-якої збіжної до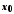 послідовності значень аргументу
послідовності значень аргументу ,
відмінних від
,
відмінних від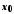 ,
відповідна послідовність значень
функції збігається до числа
,
відповідна послідовність значень
функції збігається до числа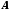 .
Символічно
це записують так:
.
Символічно
це записують так:
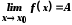 .
Означення
границі функції за Коші.
Нехай функція
.
Означення
границі функції за Коші.
Нехай функція
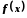 визначена в деякому околі точки
визначена в деякому околі точки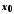 ,
крім, можливо, самої точки
,
крім, можливо, самої точки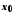 .
Число
.
Число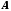 називається границею функції
називається границею функції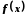 у точці
у точці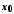 ,
якщо для довільного числа
,
якщо для довільного числа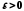 існує число
існує число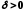 таке, що нерівність
таке, що нерівність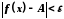 виконується для всіх
виконується для всіх ,
що задовольняють умову
,
що задовольняють умову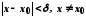 .
.
Означення границі функції за Гейне і за Коші еквівалентні.
Дійсно, нехай
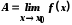 згідно з Гейне. Покажемо, що в цьому
випадку для довільного числа
згідно з Гейне. Покажемо, що в цьому
випадку для довільного числа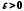 існує число
існує число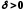 таке, що нерівність
таке, що нерівність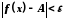 виконується для всіх
виконується для всіх ,
що задовольняють умову
,
що задовольняють умову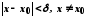 ,
тобто що
,
тобто що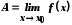 згідно з означенням Коші.
згідно з означенням Коші.
Припустимо
протилежне. Нехай існує
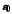 таке, що для довільного
таке, що для довільного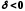 існує точка
існує точка![]() ,
для якої з умови
,
для якої з умови![]() випливає нерівність
випливає нерівність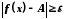 .
Розглянемо послідовність
.
Розглянемо послідовність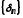 ,
де
,
де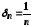 .
Виберемо точки
.
Виберемо точки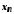 такі, що
такі, що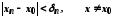 (1)
і
(1)
і
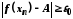 .
(2)
.
(2)
Оскільки
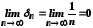 ,
то
,
то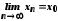 ,
але за нерівністю (2)
,
але за нерівністю (2)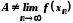 ,
що суперечить умові, тобто що
,
що суперечить умові, тобто що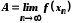 згідно з Гейне.
згідно з Гейне.
Нехай тепер
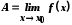 згідно з Коші. Покажемо, що
згідно з Коші. Покажемо, що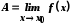 і згідно з Гейне.
Отже, нехай
для будь-якого
і згідно з Гейне.
Отже, нехай
для будь-якого
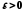 існує число
існує число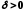 таке, що із нерівності
таке, що із нерівності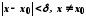 випливає нерівність
випливає нерівність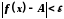 .
Виберемо довільну послідовність точок
.
Виберемо довільну послідовність точок збіжну до
збіжну до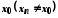 .
Тоді для значення
.
Тоді для значення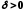 ,
відповідного
,
відповідного ,
знайдеться такий номер
,
знайдеться такий номер ,
що для всіх
,
що для всіх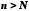 виконуватимуться нерівності
виконуватимуться нерівності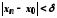 і разом із тим
і разом із тим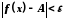 .
Оскільки вибір
.
Оскільки вибір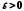 був довільним, то це означає, що для
довільної послідовності
був довільним, то це означає, що для
довільної послідовності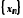 із умови
із умови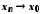 випливає умова
випливає умова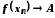 ,
тобто що
,
тобто що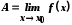 за Гейне.
за Гейне.
Еквівалентність означень границі функції за Гейне і за Коші дає можливість використовувати будь-яке із них залежно від того, яке є більш зручним для розв'язування тієї чи іншої задачі.
Число
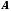 називається границею функції
називається границею функції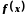 у точці
у точці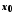 справа (зліва), якщо для будь-якої збіжної
до
справа (зліва), якщо для будь-якої збіжної
до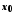 послідовності
послідовності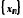 ,
елементи якої більші (менші)
,
елементи якої більші (менші)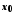 ,
відповідна послідовність
,
відповідна послідовність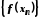 збігається до числа
збігається до числа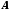 .Символічно:
.Символічно: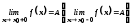 .
Функція
.
Функція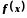 має в точці
має в точці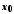 границю тоді й тільки тоді, коли в цій
точці існує як права, так і ліва границя
та ці границі рівні між собою. У цьому
випадку границя функції дорівнює
одностороннім границям.
границю тоді й тільки тоді, коли в цій
точці існує як права, так і ліва границя
та ці границі рівні між собою. У цьому
випадку границя функції дорівнює
одностороннім границям.
Границя
функції на нескінченності. Число
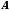 називається границею функції
називається границею функції при
при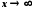 , якщо для будь-якої нескінченно великої
послідовності
, якщо для будь-якої нескінченно великої
послідовності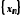 значень аргументу відповідна послідовність
значень аргументу відповідна послідовність значень функції збігається до числа
значень функції збігається до числа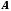 .
(
.
(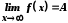 ).
).
Властивості
неперервних функцій: Якщо
функція
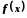 має границю в точці
має границю в точці ,
то ця границя єдина; Якщо функції
,
то ця границя єдина; Якщо функції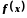 і
і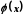 мають у точці
мають у точці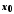 границі, то функції
границі, то функції (при
(при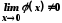 )
у точці
)
у точці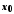 також мають границі, причому
також мають границі, причому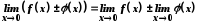 ;
(3)
;
(3)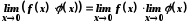 ;(4)
;(4) (5) ; Якщо функції
(5) ; Якщо функції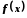 і
і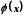 ,
визначені в деякому околі точки
,
визначені в деякому околі точки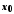 ,
крім, можливо, самої точки
,
крім, можливо, самої точки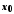 ,
мають у точці
,
мають у точці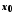 границі, й такі, що в околі точки
границі, й такі, що в околі точки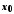
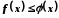 .
Тоді
.
Тоді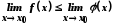 ;
Якщо функції
;
Якщо функції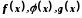 визначені в деякому околі точки
визначені в деякому околі точки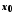 ,
крім, можливо, самої точки
,
крім, можливо, самої точки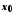 ,
функції
,
функції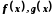 мають у точці
мають у точці границю, рівну
границю, рівну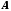 ,
тобто
,
тобто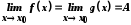 .
Нехай, крім того, виконується нерівність
.
Нехай, крім того, виконується нерівність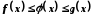 .
Тоді функція
.
Тоді функція![]() у точці
у точці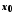 має границю, рівну
має границю, рівну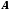 ,
тобто
,
тобто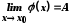 ;
;
