Случайная выборка. Определение средней ошибки при нахождении среднего значения признака в генеральной совокупности

При нахождении среднего значения признака по генеральной совокупности формулы для средней ошибки используются следующие:

Повторная случайная выборка

= ;

Бесповторная случайная выборка

=

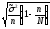
Из формул видно, что средняя ошибка меньше у бес­повторной выборки, что и обусловливает ее более широкое применение.

Определение средней ошибки при нахождении доли с определенным значением признака в генеральной совокупности

Когда требуется узнать долю значений с определенными значением признака в генеральной совокупности, рассчитывают дисперсию для доли и подставляют её вместо дисперсии для значения признака.

Выборочная дисперсия для доли с определенным значением признака рассчитывается по следующей формуле:

После этого рассчитываем среднюю ошибку:

Повторная случайная выборка

;

Бесповторная случайная выборка

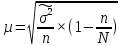
Определение необходимой численности выборочной совокупности для достижения заданной предельной ошибки выборки

Часто при разработке программы выборочного наблюдения определяется конкретное значение предельной ошибки с заданным уровнем вероятности. Не­известной при этом остается минимальная численность выборки, обеспечиваю­щая заданную точность.

Необходимую численности выборки можно определить по формулам.

для повторной выборки n = ;

для бесповторной выборки n = .

При определении необходимой численности выборки для определения доли значений в генеральной совокупности с определенным значением признака вместо общей дисперсии по выборке в формуле используют общую дисперсию доли по выборке.

Определение вероятности предполагаемого значения показателей

Для определения вероятности выбранных значений необходимо найти коэффициент t, используя который находим вероятность события по таблице удвоенной нормированной функции Лапласа. Определяется t по формуле.

;

Такие же формулы применяются для механической выборки.

Типическая выборка

При определении средней ошибки типической выборки используется

^{случайная (внутригрупповая}) дисперсия по выборке ^.

^{Средняя ошибка выборки определяется по следующим формулам:}

^{Типическая повторная выборка:}

типическая бесповторная выборка

Напомним формулу случайной дисперсии:

Где – дисперсия, рассчитанная внутри i-ой группы,

- количество элементов в i-ой группе (частота группы),

n – число элементов во всей выборке

Случайная дисперсия для доли значений по выборке рассчитывается аналогично

где Где – дисперсия доли, рассчитанная внутри i-ой группы выборки,

- количество элементов в i-ой группе (частота группы),

n – число элементов во всей выборке

Выборочная дисперсия для доли с определенным значением признака рассчитывается по следующей формуле:

Повторная случайная выборка

;

Бесповторная случайная выборка

Серийная выборка

При вычислении средней ошибки выборки при серийном отборе используется факторная (межгрупповая) дисперсия. Вместо понятия количество элементов в выборке (n) применяется понятие число отобранных серий (групп) в выборке (m). Серии могут быть равновеликие (во всех сериях одинаковое количество элементов) и неравновеликие (в всех сериях неодинаковое количество элементов). Чаще всего применяется отбор с равновеликими сериями, поэтому формулы приведены именно для этого случая.

Формула межгрупповой дисперсии для серийной выборки (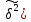в несколько преобразованном виде при вычислении интервалов значений признака выглядит так:

,

Где - среднее значение признака в i-ой серии

- среднее значение по всей выборке,

- число равновеликих серий в выборке.

При расчете среднего значения изучаемого признака cредняя ошибка выборки рассчитывается по следующим формулам:

Для повторной выборки:

Для бесповторной выборки

При определении доли с определенным значением признака факторную дисперсию находят по следующей формуле:

Где – доля значений с определенным значением признака в i-ой серии

- доля значений с определенным значением признака по всей выборке,

- число равновеликих серий в выборке.

При расчете доли элементов с определенным значением признака cредняя ошибка выборки рассчитывается по следующим формулам:

Для повторной выборки:

Для бесповторной выборки