
Розділ 3. Геометрія
Приклад
3.1. Знайти
координати точки К,
яка
симетрична точці M(2;
-1) відносно
прямої


Точка
К
лежить
на прямій
 ,
яка проходить через точку М
і
перпендикулярна прямій
,
яка проходить через точку М
і
перпендикулярна прямій
 Рівняння прямої
Рівняння прямої має вигляд
має вигляд
 (покажіть
це!).
(покажіть
це!).
Знаходимо
координати точки N
– точки
перетину прямих l
і




Використовуючи
формулу координат середини відрізка,
знаходимо координати точки


Відповідь:

Приклад 3.2.
Записати:
а) рівняння бісектриси AL трикутник ABC;
б) рівняння кола, вписаного в трикутник ABC,
якщо
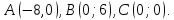

Згідно властивості бісектриси AL трикутника ABC маємо:
CL : LB = AC : AB = 8 : 10 = 4 : 5.
Знаходимо
координати точки
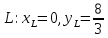 .
.
Рівняння прямої l має вигляд:

Оскільки центр O кола, вписаного в трикутник ABC, являється точкою перетину бісектрис, то його координати задовольняють систему рівнянь


Отже, рівняння кола вписаного в трикутник ABC має вигляд:


Відповідь:
а)

Приклад
3.3.
Вектори
 утворюють
кут
утворюють
кут
 і
і

Обчислити
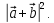

Відповідь: 103
Приклад
3.4.
Який
кут (у градусах) утворюють одиничні
вектори
 і
і
 взаємно
перпендикулярні?
взаємно
перпендикулярні?

Відповідь:

Приклад
3.5.
Опуклий
чотирикутник поділяється на чотири
трикутники; площі трьох з них відповідно
дорівнюють 10,20 і 30
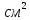 ,
та кожна з цих площ менше площі четвертого
трикутника. Знайти заданого чотирикутника.
,
та кожна з цих площ менше площі четвертого
трикутника. Знайти заданого чотирикутника.
Нехай

За умовою маємо:


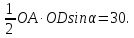
Враховуючи,
що
 запишемо:
запишемо:

Перемноживши ці рівності матимемо:



Підставляючи значення

Тоді

Відповідь:
120

Приклад 3.6. В трикутнику ABC величина кута A вдвічі більше величини кута B, а довжина сторін, протилежних цим кутам, дорівнюють відповідно 12 і 8 см. Знайти довжину третьої сторони трикутника.
Нехай
 тоді
тоді

За
теоремою косинусів

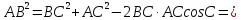
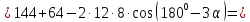

За
теоремою синусів


Тоді

Відповідь: 10 см.
Приклад 3.7. У рівнобедрений трикутник вписано коло. Точки дотику поділяють кожну бічну сторону на відрізки довжиною m і n, рахуючи від вершини. До кола проведені три дотичні, паралельні кожній із сторін трикутника. Знайти довжини відрізків дотичних, обмежених сторонами трикутника.
Нехай


AD=AE=n і CD=CG=n, як дотичні до кола, які
входять з однієї точки. Отже,


(SE=SF як дотичні до кола, які виходять з однієї точки) або



або, оскільки

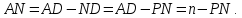
(RE=RP,ND=PN, як дотичні до кола, які входять з однієї точки), то
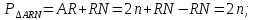


Відповідь:
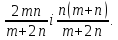
Приклад 3.8. У трикутник зі сторонами 6,10 і 12 см вписано коло. До кола проведено дотичну так, що вона перетинає дві більші сторони трикутника. Знайти периметр трикутника який відтинається дотичною.
Нехай


BC=12 см, DE – дотична до кола.



 Фігура
ABED
Фігура
ABED –
описаний
чотирикутник, отже,
–
описаний
чотирикутник, отже,
 Підставляючи
значення
Підставляючи
значення
 у
рівність (*), маємо
у
рівність (*), маємо

Відповідь: 16 см.
Приклад
3.9.
У трикутнику ABC
задано
гострі кути
 і
і

 при основіAC.
З вершини B
проведені
висота BD
та
бісектриса BE.
Знайти
площу трикутника BDE,
якщо
площа трикутника ABC
дорівнює S.
при основіAC.
З вершини B
проведені
висота BD
та
бісектриса BE.
Знайти
площу трикутника BDE,
якщо
площа трикутника ABC
дорівнює S.

За
умовою
 звідки
звідки

З прямокутних трикутників BDA і BDC знайдемо
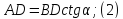

Додавши рівності (2) і (3):
AC=AD+CD=BDctg +BDctg
+BDctg =BD(ctg
=BD(ctg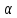 +ctg
+ctg ).(4)
).(4)
Підставляючи значення AC з (4) в (1), отримуємо:
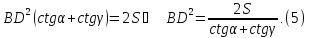
У
трикутнику ABC
маємо
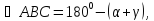 тоді
у трикутнику ABE:
тоді
у трикутнику ABE:
 Далі,
в прямокутному трикутнику BDE
маємо:
Далі,
в прямокутному трикутнику BDE
маємо:

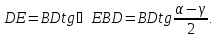
Тоді площа трикутника BDE дорівнює:

Підставляючи
значення
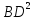 з
(5) у (6), отримаємо
з
(5) у (6), отримаємо

Скориставшись формулою

знаходимо площу трикутника

Відповідь:
 .
.
Приклад 3.10.
Сторони
паралелограма відповідно дорівнюють
a
і
b
, (a<b).
Із
середини більшої сторони паралельну
сторону видно під кутом
 .
Знайти площу паралелограма.
.
Знайти площу паралелограма.
За
умовою,


Позначимо

Тоді
 і
в трикутниках BEC,
BAE
і
CDE,
за
теоремою косинусів, маємо
і
в трикутниках BEC,
BAE
і
CDE,
за
теоремою косинусів, маємо
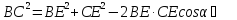




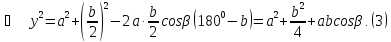
Додамо почленно рівності (2) і(3). Отримаємо
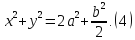
А
тепер значення
 з
(4) підставимо в (1).
з
(4) підставимо в (1).
Отже,

Тоді площа паралелограма ABCD дорівнює

або,
оскільки
 то
то
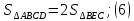

Підставляючи
значення
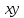 з
(5) у (7), маємо:
з
(5) у (7), маємо:

Отже,
тепер підставляючи значення
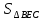 з
(8) у (6), знаходимо площу
з
(8) у (6), знаходимо площу

Відповідь:
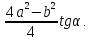
Приклад 3.11.
На
відрізку AC
задано
точку
B,
причому
AB=14
см,
BC=28
см. На відрізках AB,BC
і
AC,
як
на діаметрах, побудовані півкола в одній
півплощині щодо AC.
Знайти
радіус кола, яке дотикається всіх трьох
півкіл.
Нехай OB=7 см, BP=14 см, AQ=21см, SF=x см – радіуси відповідних кіл. Точки дотику знаходяться на лініях, які з`єднають центри.
Отже,

Оскільки

За теоремою косинусів:

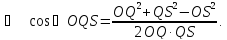


Тоді


Відповідь: 6 см.
Приклад 3.12. У трапецію, у якої менша основа дорівнює a, вписано коло.
Одна
з бічних сторін трапеції поділяється
точкою дотику на відрізки довжиною m
і n,
якщо
рахувати від більшої основи. Визначити
площу трапеції. 
Нехай
 – радіус
кола, вписаного в трапецію ABCD.
З`єднаємо
центр кола
O
з
точками
– радіус
кола, вписаного в трапецію ABCD.
З`єднаємо
центр кола
O
з
точками

Трикутники
AOB
і
COD
–
прямокутні і

Проведемо
 Висота,
проведена з вершини прямого кута, є
середнім пропорційним між проекціями
катетів на гіпотенузу.
Висота,
проведена з вершини прямого кута, є
середнім пропорційним між проекціями
катетів на гіпотенузу.
Отже, в трикутнику AOB:

Тоді, висота трапеції

У трикутнику COD:

Порівнявши (1) і (2), отримаємо:


Площа трапеції ABCD дорівнює:

Відповідь:

Приклад
3.13. Навколо
кола радіуса
R=1
см
описана рівнобічна трапеція, площа якої
дорівнює 5
 .
Знайти площу чотирикутника, вершинами
якого служать точки дотику кола та
трапеції.
.
Знайти площу чотирикутника, вершинами
якого служать точки дотику кола та
трапеції.
Нехай
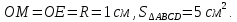

Площа
трапеції


В
опуклий чотирикутник можна вписати
коло, тоді і тільки тоді, коли суми
протилежних сторін чотирикутника рівні.
Отже,


З прямокутного трикутника ABP маємо:



Оскільки

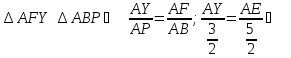

Отже, площа чотирикутника дорівнює:


Підставляючи
в останню рівність значення
 маємо:
маємо:
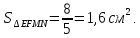
Відповідь:

Приклад 3.14. Відстань від правильної чотирикутної піраміди до бічної грані і до бічного ребра відповідно дорівнюють a і b. Знайти двогранний кут при основі піраміди.
Нехай
SABCD
– задана піраміда, SO
– висота піраміди.
 де
де
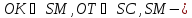 через
через
 а
кут SCO
через
а
кут SCO
через

З прямокутного трикутника OKM знайдемо:

З прямокутного трикутника CMO, за теоремою Піфагора:

Далі з прямокутних трикутників SOM і SOC знайдемо


Порівнюючи праві частини рівностей (1) і(2), отримуємо,


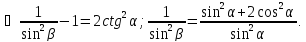
Тоді

З прямокутного трикутника OTC матимемо

Підставимо
значення

Отже,
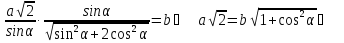


Відповідь:

Приклад
3.15. Сторони
нижньої та верхньої основ правильної
трикутної зрізаної піраміди відповідно
дорівнюють
a
і
b,
(a>b).
Бічна грань утворює з площиною основи
кут, рівний
 .
Знайти площу перерізу піраміди площиною,
який проходить через середню лінію
бічної грані і центр нижньої основи.
.
Знайти площу перерізу піраміди площиною,
який проходить через середню лінію
бічної грані і центр нижньої основи.
Нехай
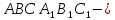 задана
піраміда,
задана
піраміда,
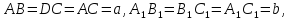
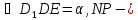 середня
лінія бічної грані
середня
лінія бічної грані
 центр
верхньої основи,O
– центр нижньої основи,
центр
верхньої основи,O
– центр нижньої основи,
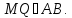

Радіус
кола, описаного навколо правильного
трикутника ABC,
дорівнює

З прямокутного трикутника COQ:
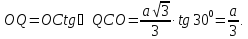
Отже,
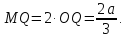
Проведемо
 і
з прямокутного трикутника
і
з прямокутного трикутника


Далі, з трикутника OKD:
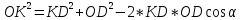
Отже:



Відповідь:
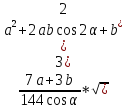
Приклад
3.16. У правильній
трикутній піраміді бічна грань має
задану площину та утворює з площиною
основи кут
 .
При якому значенні
.
При якому значенні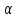 відстань від центра основи піраміди до
бічної грані буде найбільшою?
відстань від центра основи піраміди до
бічної грані буде найбільшою?
Нехай
SABC–задана
піраміда, ∠SDO=α,
де SD
⫠
AC,
BD
⫠
AC
i
AD
= CD,
OK⫠SD.
Позначимо
площу бічної грані SAC
через S
,
тоді, згідно властивості ортогональності
проекції плоского багатокутника, маємо:
 (1)
(1)
З прямокутного трикутника ODC знайдемо:

Підставивши
це значення  у
(1), отримаємо:
у
(1), отримаємо:
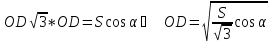
Отже, з прямокутного трикутника OKD:

Побудуємо функцію, найбільше значення якої потрібно знайти:

У
даному випадку кут α – гострий, а, отже,
α ϵ(0; ).
).
Далі
задача зводиться до пошуку найбільшого
значення функції f(α)
на проміжку (0; ).
).
Відповідь:
arctg .
.
Приклад 3.17. Відношення об’єму зрізаного конуса до об’єму вписаної в нього кулі дорівнює k. Знайти кут між твірною конуса і площиною його основи та допустимі значення k.
Розглянемо
осьовий переріз заданих тіл. AA1B1B
– рівнобічна трапеція, AA1
= B1B,
O’ – центр
вписаного кола, B1E
– висота. Покладемо О’О1
= О’О = O’D
= r, де
О’D⫠B1B,
∠B1BO
= α.
Тоді O1B1+OB
= B1D+BD
= B1B.
З прямокутного трикутника B1EB:


Далі
з прямокутного трикутника
B1O’B( B1O’B=90°)
маємо
B1O’B=90°)
маємо
B1D*BD = O’D2 ⟺ O1B1*OB = r2.
Отже,
O1B1+OB
=
 .За
умовою:
.За
умовою:
 =k;
=k;

Де
має бути k
>
 .
.
Відповідь:
 .
.
Приклад 3.18. У конус із заданим об’ємом вписана піраміда; в основі якої лежить рівнобедрений трикутник, у якого величина кута при вершині дорівнює α. При якому значенні α об’єм піраміди буде найбільшим?
Об’єм
конуса дорівнює: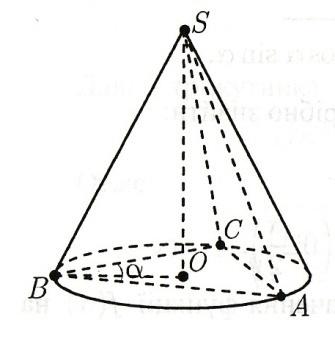

де OB – радіус основи конуса і описаного навколо трикутника ABC кола, SO – висота.
Згідно наслідку з теореми синусів, маємо
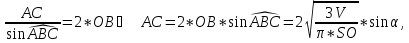
А за теоремою косинусів, у трикутнику ABC маємо

Враховуючи, що AB = BC, маємо
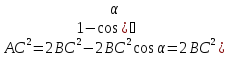


Побудуємо функцію, найбільше значення якої потрібно знайти:
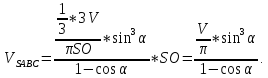
У цьому випадку α ϵ (0;π). Отже, задача зводиться до відшукання найбільшого значення функції V(α) на проміжку (0;π).
Відповідь:

Приклад
3.19 Сторона
основи правильної чотирикутної піраміди
дорівнює a,
а
двогранний кут при основі дорівнює α.
Знайти відстань від центра сфери,
вписаної в цю піраміду, до бічного ребра.

 –задана
піраміда,
–задана
піраміда,
 –
апофеми,
–
апофеми,
 -
висота піраміди,
-
висота піраміди,
 - точка
дотику кулі до бічної грані
- точка
дотику кулі до бічної грані
 .
Точка
.
Точка
 – центр кола, вписаного в трикутник
– центр кола, вписаного в трикутник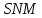 лежить на перетині бісектрис. Отже,
лежить на перетині бісектрис. Отже, - бісектриса кута
- бісектриса кута ,
тобто
,
тобто

З
прямокутного трикутника
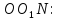


А
з прямокутного трикутника
 знайдемо:
знайдемо:

Далі,
з
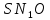 отримаємо
отримаємо а в прямокутному трикутнику
а в прямокутному трикутнику за теоремою Піфагора, визначимо
за теоремою Піфагора, визначимо
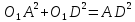 і
оскільки
і
оскільки
 то
то

Тоді
з прямокутного трикутника


Оскільки прямокутні трикутники SKO і SO1D подібні (вони мають спільний кут DSO1), K основа перпендикуляра упущеного з О на SD, то

Відповідь:

Приклад
3.20 У
правильну зрізану трикутну піраміду
вписано дві кулі: одна дотикається всіх
її граней, друга – всіх ребер. Знайти
синус кута між бічним ребром і площиною
основи.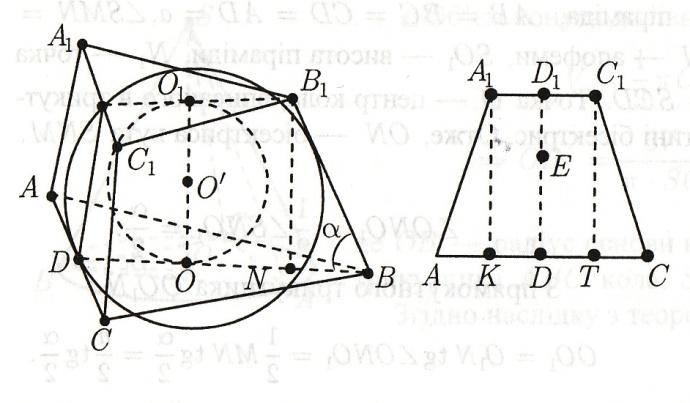
Нехай
ABCA1B1C1
– задана піраміда. Позначимо: AB=BC=AC=a,
A1B1=
B1C1=
A1C1=a1,
AA1=
BB1=
CC1=l,
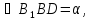 де
D1D
– апофема, BD⫠AC.
де
D1D
– апофема, BD⫠AC.
Куля, вписана в піраміду, дотикається її основ ABC і A1B1C1 у центрах О і О1 , а також апофеми D1D у точці Е.
Проведемо A1K ⫠AC I C1T||A1K. Тоді

З прямокутного трикутника А1КА, за теоремою Піфагора, знайдемо
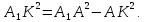
Або,
оскільки А1К
= D1D,
то

З
трикутників А1В1С1
і АВС, знайдемо

Тоді, так як DE=OD i D1E=O1D1, то
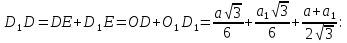

Порівнюючи праві частини (1) і (2), отримуємо

Оскільки друга куля дотикається до всіх ребер піраміди, то грань AA1C1С перетинає її так, що в перерізі утворюється коло, вписане в трапецію AA1C1С. Для того, щоб в опуклий чотирикутник можна було вписати коло, необхідно і достатньо, щоб суми протилежних сторін, цього чотирикутника, були рівні. Отже,
A1C1+AC=A1A+C1C⇔a1+a=l+l, a1+a=2l. (4)
Розв’язуючи рівняння (3) і (4), знайдемо, що при

Далі, проведемо B1N⫠BN.
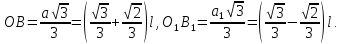
Тоді

З
прямокутного трикутника В1 знайдемо:
знайдемо:

Піднесемо обидві частини рівності до квадрату:

Тоді

Відповідь:
Приклад
3.21 Поверхня
кулі, вписаної в правильну зрізану
трикутну піраміду, відноситься до повної
поверхні піраміди, як
 .
Знайти кут між бічною гранню і площиною
основи піраміди.
.
Знайти кут між бічною гранню і площиною
основи піраміди.
Позначимо
А1В1=В1С1=А1С1=а1,
АВ=ВС=АС=а, О2О1=О2О=R,
де
R
– радіус кулі,
 а
О1
і О – центр трикутників ABC
і A1B1C1.
Знайдемо точки О2
і D,
О2
і D1,
де О2
– центр кулі.
а
О1
і О – центр трикутників ABC
і A1B1C1.
Знайдемо точки О2
і D,
О2
і D1,
де О2
– центр кулі.
Розглянемо осьовий переріз DD1В1В заданих тіл:
O1D1+OD=D1K+DK=
D1
D
і
з прямокутного трикутника D1ED
( )знайдемо
)знайдемо

Далі,
в прямокутному трикутнику
 (
( )знайдемо:
)знайдемо:
D1K*DK=O2K2(O2K⫠D1D);
O1D1*OD=R2.
За умовою ,

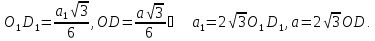
Тоді отримуємо:
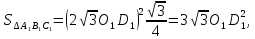



Отже (1) матиме вигляд:

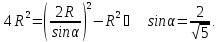
Відповідь:
