Завдання до теми

Визначити тип ДРЧП та зробити зведення до канонічного вигляду: .

Розв’язування. У даному випадку ,,, тобто рівняння гіперболічного типу.

Рівняння характеристик має вигляд: =3 або= -1.

Звідси отримуємо два лінійно незалежних інтеґрала і. Уводячи нові змінні,будемо мати:

*2

*6

*1

*2

*(-3)

Підставивши знайдені вирази до даного диференціального рівняння, отримуємо:

–перша канонічна форма гіперболічного рівняння.

Завдання для перевірки знань

Визначити тип ДРЧП та зробити зведення до канонічного вигляду.

• . Відповідь: .

• . Відповідь: .

• . Відповідь: .

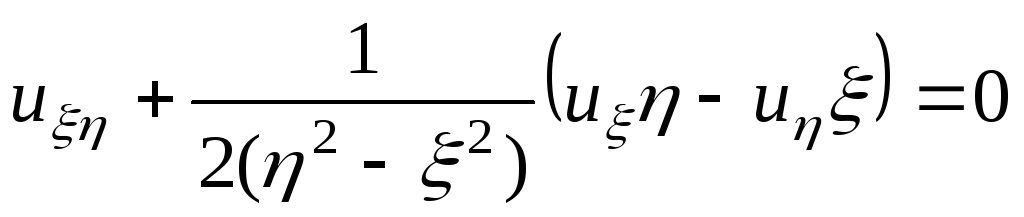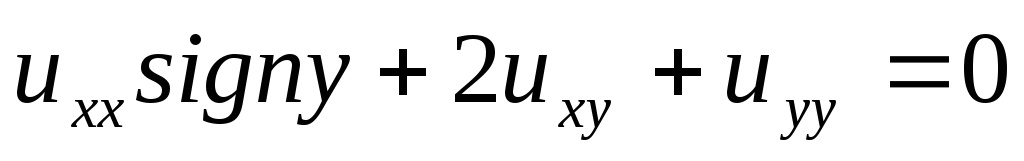• . Відповідь: а) , б).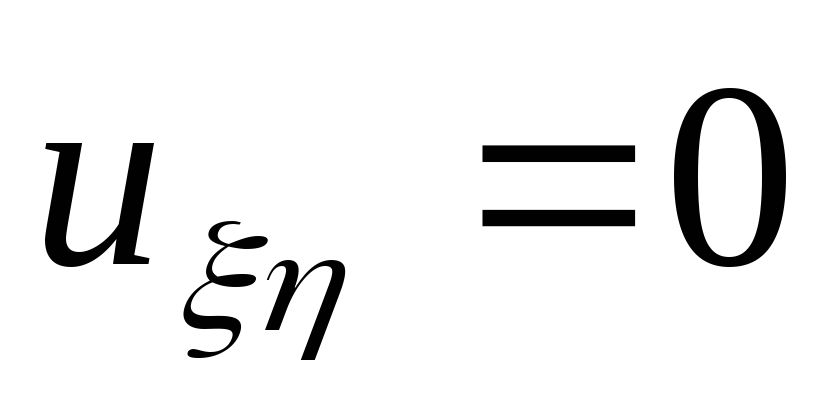

Контрольні питання

• У якому випадку рівняння (1) називається однорідним?

• Які рівняння називаються канонічними?

• Як проводиться класифікація ДРЧП вигляду (1)?

Література: [1, 6].

Практичне заняття № 4

Тема Спрощення канонічних форм лінійних ДРЧП 2-го порядку зі сталими коефіцієнтами

Мета: засвоїти типи ДРЧП 2-го порядку та навчитися спрощувати канонічний вигляд ДРЧП 2-го порядку.

Короткі теоретичні відомості

Залежно від типу лінійне ДРЧП 2-го порядку зі сталими коефіцієнтами зводиться до однієї із канонічних форм. Подальшого спрощення цих канонічних форм можна досягти, якщо зробити заміну:

…, (1)

де – нова шукана функція,і– сталі, які відшукуються з умов, щоб коефіцієнти біля перших похідних функціїдля рівнянь гіперболічного та еліптичного типів дорівнювали нулю. У разі рівняння параболічного типу нулеві дорівнюють один із коефіцієнтів перших похідних та коефіцієнт біля самої функції. Таким чином, отримаємо рівняння вигляду:

• –гіперболічний тип; (2)

• –еліптичний тип; (3)

• –параболічний тип. (4)

Завдання до теми

Звести до канонічної форми та зробити подальше її спрощення: .

Розв’язування. У даному випадку ,,, тобто рівняння еліптичного типу.

Рівняння характеристик має вигляд: .

Звідси отримуємо . Уводячи нові змінні,будемо мати:

*(-4)

*1

*2

*2

*1

Підставивши знайдені вирази до даного диференціального рівняння, отримуємо:

–канонічна форма еліптичного рівняння.

Зробивши заміну , де,– невизначені коефіцієнти, будемо мати:

*6

*4

*1

*1

Підставивши отримані значення до рівняння та скоротивши на , будемо мати

.

Визначаємо татак, щоб коефіцієнти притаперетворювалися на нуль.

При таких значеннях тарівняння перетвориться в наступне

–канонічне рівняння еліптичного типу.

Завдання для перевірки знань:

Звести до канонічної форми та зробити подальше її спрощення:

• . Відповідь: ,,.

• . Відповідь: .

Контрольні питання

• Дайте визначення лінійного ДРЧП 2-го порядку зі сталими коефіцієнтами.

• Використовуючи (1), виразити похідні першого та другого порядків функції через похідні функції.

• Вигляд (3) – це єдина можливість для рівнянь еліптичного типу?

Література: [1-4].

Практичне заняття № 5

Тема Контрольна робота № 1.

Мета: контроль отриманих знань з тем:

• диференціальні рівняння в частинних похідних (ДРЧП) 1-го порядку. Загальний розв’язок;

• ДРЧП 1-го порядку. Задача Коші;

• класифікація ДРЧП 2-го порядку та зведення до канонічного вигляду;

• спрощення канонічних форм лінійних ДРЧП 2-го порядку зі сталими коефіцієнтами.

Завдання для перевірки знань

Звести до канонічного вигляду та провести подальше спрощення канонічної форми наступних рівнянь:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

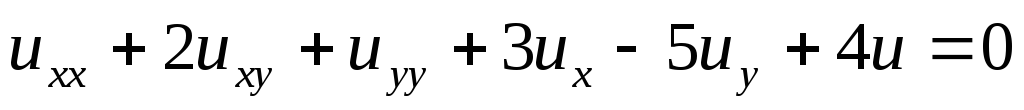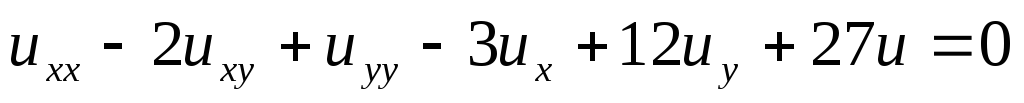10) ;

11) ;

12) ;

13) ;

14) ;

15) .

Література: [1, 6].

Практичне заняття № 6

Тема Метод характеристик для рівнянь гіперболічного типу. Задача Коші

Мета: дати уявлення про задачу Коші.для рівнянь гіперболічного типу. Виробити навички розв’язку задачу Коші. методом характеристик.

Короткі теоретичні відомості

• Відшукування загального розв’язку методом характеристик.

У випадку, коли гіперболічне рівняння має першу канонічну форму у вигляді , його загальний розв’язок відшукують таким чином:

Нехай . Тодіфункціянезалежна від. Проінтеґруючи останній вираз, отримуємо. Таким чином, загальний розв’язок має вигляд, де =.

• Розв’язок задачі Коші методом характеристик.

У випадку розв’язування задачі Коші для гіперболічного рівняння з початковими умовами необхідно спочатку знайти загальний розв’язок рівняння, а потім визначитиітак, щоб вони задовольняли початкові умови.