3. Порядок выполнения работы

1. Выполнить решение примера индивидуального задания (с.79) в Excel.

4.3. Блок текущего контроля

4.3.1. Репетиционный тест по разделу 1

1. Вычислите и определите погрешность результата 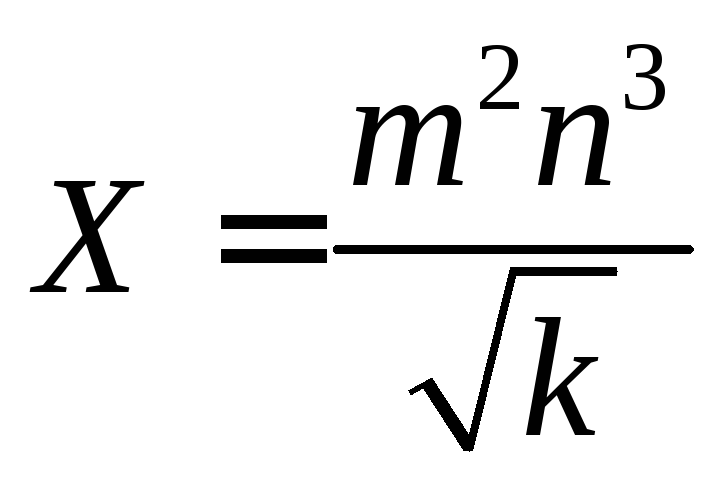, где. Воспользуйтесь расчетными формулами для абсолютнойи относительнойпогрешностей приближённого числа:,, ,,,,,.

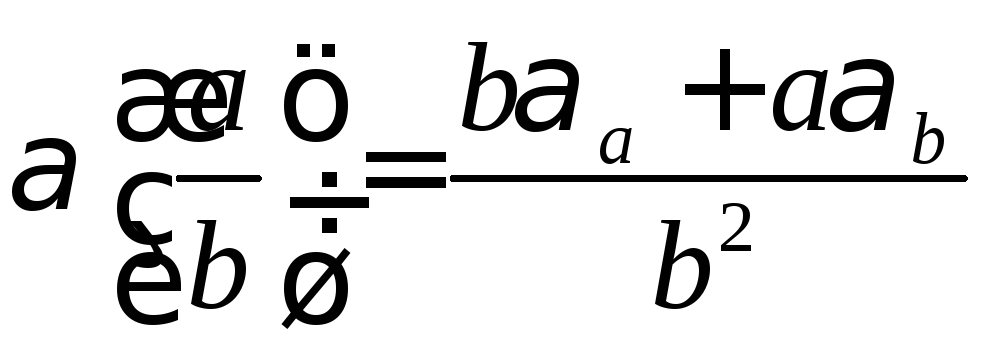A.
B.
C.
D.

2. Укажите, сколько узловых точек нужно иметь для построения интерполяционного многочлена Ньютона пятой степени.

A.	3
B.	4
C.	5
D.	6

3. Постройте интерполяционный полином третьей степени для функции, заданной таблицей. Найдите приближённое значение функцииприс помощью полученного полинома.

		0,5	0,7		0,9	1,1
		0,6915	0,7580		0,8159	0,8643
A.	0,5749
B.	0.0176
C.	1,126
D.	0,771206

4. Определите, сколько положительных корней иметь уравнение .

A.	B.	C.	D.	E.
3	2	1	0

5. Отделите вещественный корень уравнения и найдите его приближённое значение.

A.	1,516
B.	-1,516
C.	1,496
D.	1,389

6. Вычислите приближённо определённый интеграл за шесть шагов методом Симпсона и оцените погрешность вычисления.

A.	0,4041339±0,0000167
B.	0,404±0,00001
C.	0,40413±0,00001
D.	0,40±0,01

7. Проинтегрируйте методом Эйлера уравнение с начальным условиемна отрезкес шагом.

Верный ответ:

ОТВЕТЫ

1. А, B; 2. D; 3. D; 4. D; 5. A; 6.A;

4.3.2. Репетиционный тест по разделу 2

1. Вычислите модуль и главное значение аргумента к.ч. .

A.	5; 53,130
B.	-5; 53,130
C.	5; -53,130
D.	-5; -53,130

2. Выделите вещественную и мнимую части функции .

A.
B.
C.
D.

3. Вычислите производную функции f(z) в точке = i, если f(z) = Sin z.

A.	1,543
B.	-1,543
C.	-3,14
D.	3,14

4. Найдите регулярную функцию , если известна её мнимая часть и.

A.
B.
C.
D.

5. Вычислите интеграл

A.
B.
C.
D.

6. Вычислите интеграл , где– участок параболына отрезке.

A.
B.
C.
D.

7. Вычислите интеграл , где– произвольный замкнутый контур, обходящий точкув положительном направлении.

A.
B.
C.
D.

8. Разложите функцию в степенной ряд, используя известное разложение для.

A.
B.
C.
D.	1

9. Найдите особые точки функции .

A.	– полюсы 1-го порядка;– полюс 2-го порядка; – существенно особая точка
B.	– существенно особые точки;– полюс 2-го порядка;– существенно особая точка
C.	– полюсы 1-го порядка;– полюс 2-го порядка; – полюс 1-го порядка
D.	– полюсы 1-го порядка;– полюс 1-го порядка; – существенно особая точка

10. Вычислите вычеты функции относительно точек .

A.	– полюс 1-го порядка;– полюс 2-го порядка
B.	– полюс 1-го порядка;– полюс 2-го порядка
C.	– полюс 1-го порядка;– полюс 2-го порядка
D.	– полюс 1-го порядка;– полюс 2-го порядка

ОТВЕТЫ

1.C; 2.B; 3.A; 4.A,C; 5.D; 6.B; 7.B; 8.A; 9.A; 10.D