
- •Кафедра информатики математика ч.2 Численные методы, теория функций комплексного переменного, дискретная математика
- •1. Информация о дисциплине
- •1.2. Содержание дисциплины и виды учебной работы3
- •Раздел 1. Численные методы (59 часов)
- •Тематический план дисциплины
- •Тематический план дисциплины
- •2.3. Структурно-логическая схема дисциплины
- •3.2. Опорный конспект
- •Раздел 1. Численные методы
- •1.1. Обработка результатов измерений и погрешности вычислений
- •Вопросы для самопроверки по теме 1.1
- •1.2. Интерполяция и численное дифференцирование
- •Вопросы для самопроверки по теме 1.2
- •1.3. Численное интегрирование
- •Вопросы для самопроверки по теме 1.3
- •1.4. Приближение функций
- •Вопросы для самопроверки по теме 1.4
- •1.5. Многомерные задачи
- •1.6. Численные методы алгебры
- •Вопросы для самопроверки по теме 1.6
- •1.7. Решение систем нелинейных уравнений и задач оптимизации
- •1.8. Численные методы решения обыкновенных дифференциальных уравнений
- •Вопросы для самопроверки по теме 1.8
- •Раздел 2. Теория функций комплексного переменного
- •2.1. Комплексные числа и действия над ними
- •Вопросы для самопроверки по теме 2.1
- •2.2. Функции комплексного переменного (фкп). Условия Коши-Римана
- •Вопросы для самопроверки по теме 2.2
- •2.3. Элементарные функции и конформные отображения
- •2.4. Представление регулярных функций интегралами
- •2.5. Представление регулярных функций рядами
- •2.6. Вычеты функций и их применение
- •Раздел 3. Дискретная математика
- •3.1. Элементы теории графов
- •3.2. Формальные языки и дискретные автоматы
- •Ответ: 101001 110100. Табл.(**)
- •3.3. Элементы алгебры логики
- •Вопросы для самопроверки по теме 3.3
- •3.4. Учебное пособие
- •Раздел 4. Блок контроля освоения дисциплины
- •4.1. Методические указания к выполнению контрольных работ Контрольные работы №1 и №2
- •Варианты индивидуальных заданий
- •Контрольная работа №1 Задание 1
- •1. Цель работы
- •2. Основные теоретические положения
- •Задание 2
- •1. Цель работы
- •Задание 3
- •2.6. Метод Симпсона
- •Задание 4
- •Контрольная работа №2 Задание 5
- •Задание 6
- •Задание 7
- •Вычет в полюсе порядка m вычисляется по формуле
- •По теореме Коши о вычетах интеграл будет равен
- •Задание 8
- •Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
- •3. Порядок выполнения работы
- •2.1. Отделение корней Графический метод отделения корней
- •Решение.
- •Аналитический метод отделения корней
- •Другие методы отделения корней
- •Метод касательных (Ньютона)
- •3. Порядок выполнения работы
- •Лабораторная работа 3
- •Решение.
- •3. Порядок выполнения работы
- •Лабораторная работа 4
- •1. Цель работы
- •2. Основные теоретические положения
- •2.1. Метод прямоугольников
- •2.2. Метод трапеций
- •2.3. Метод парабол (Симпсона)
- •3. Порядок выполнения работы
- •3. Порядок выполнения работы
- •4.3. Блок текущего контроля
- •4.3.1. Репетиционный тест по разделу 1
- •4.3.2. Репетиционный тест по разделу 2
- •4.3.3. Репетиционный тест по разделу 3
- •Ответы:
- •2. Изобразить в виде графа структуру заданного языка и построить совокупность слов, порождаемых грамматикой данного языка: Алфавит . Правила грамматики:.
- •4. Построить сднф, сокращённую и минимальную днф булевой функции, заданной таблицей. Изобразить контактные схемы для исходной, сокращённой и минимальной днф.
- •4.5. Блок итогового контроля
- •4.5.1. Вопросы к зачёту
- •Глоссарий (краткий словарь основных терминов и положений)
- •Содержание
- •Раздел 1. Численные методы ………………………………… 15
Вычет в полюсе порядка m вычисляется по формуле
![]() (2)
(2)
В частности при
m=1
получим предыдущую формулу (имеем в
виду, что 0!=1, производная нулевого
порядка – сама функция); при m=2
(для полюса второго порядка)
![]()
Особая точка
называется существенно
особой точкой, если
![]() не
существует. В этом случае
resf(z0)
определяется, как коэффициент
a-1
при минус
первой степени при (z-z0)
разложения
f(z)
в ряд Лорана.●
не
существует. В этом случае
resf(z0)
определяется, как коэффициент
a-1
при минус
первой степени при (z-z0)
разложения
f(z)
в ряд Лорана.●
Пример 2.
Найти особые точки
функции
![]() .
○Эта функция имеет две особые точки
.
○Эта функция имеет две особые точки![]() и
и
![]() .
Найдем пределы функции в этих точках.
.
Найдем пределы функции в этих точках.
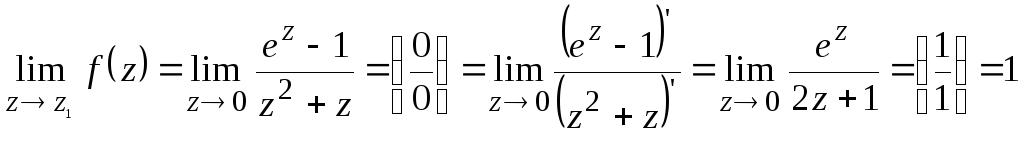 - предел конечный,
следовательно, z1=0
– устранимая особая точка. Вычет в ней
равен 0.
- предел конечный,
следовательно, z1=0
– устранимая особая точка. Вычет в ней
равен 0.
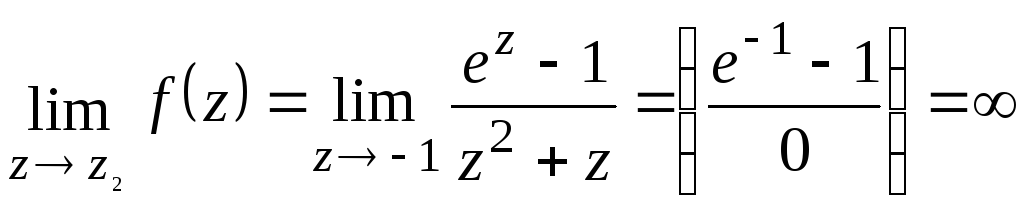 ,
следовательно, точка
,
следовательно, точка![]() – полюс. Поскольку –1 простой ноль
функции
– полюс. Поскольку –1 простой ноль
функции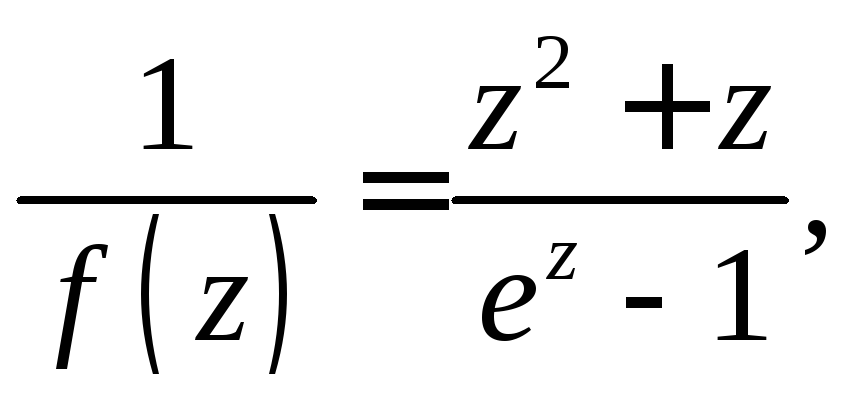 точка является простым полюсом. Вычет
в ней
точка является простым полюсом. Вычет
в ней![]() .
.
Замечание. При вычислении пределов использовалось правило Лопиталя.●
Пример 3.
Найти особые точки
функции
![]() ,
определить их тип, найти вычет в каждой
из них.
,
определить их тип, найти вычет в каждой
из них.
○f(z)
имеет три особых точки: z1=0,
z2=2i.
![]() Пределы f(z)
равны
Пределы f(z)
равны
![]() во
всех трех точках, т.е. все они полюсы.
z1=0
– полюс третьего порядка, т.к. точка
является нулем третьей кратности функции
во
всех трех точках, т.е. все они полюсы.
z1=0
– полюс третьего порядка, т.к. точка
является нулем третьей кратности функции
![]() ,
а точкиz2=2i
и
,
а точкиz2=2i
и
![]() –
полюса второго порядка, т.к. они двукратные
нули функции
–
полюса второго порядка, т.к. они двукратные
нули функции
![]() .
.
Найдем вычеты в этих точках по формуле (2).
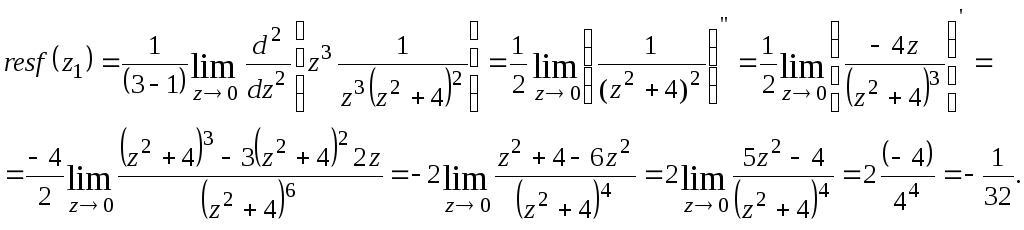
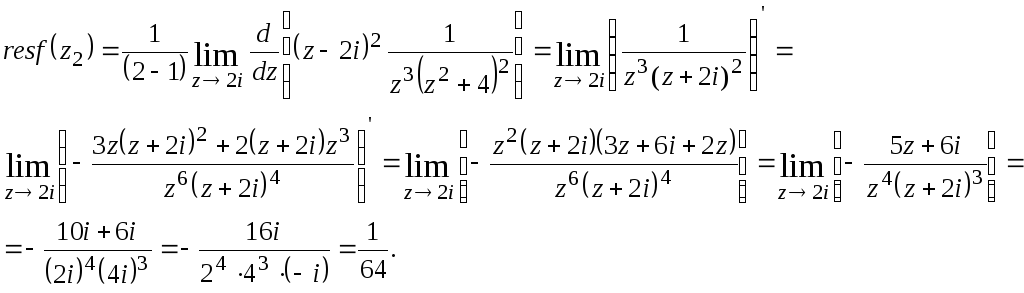

●
Пример 4.
Вычислить интеграл
![]()
○Чтобы вычислить интеграл по замкнутому контуру нужно воспользоваться таким алгоритмом.
Определить контур интегрирования на комплексной плоскости, указав положительное направление обхода контура.
Найти особые изолированные точки внутри контура интегрирования, определить их тип и вычислить вычеты в этих точках.
Вычислить интеграл по теореме Коши о вычетах.
В рассматриваемом
примере контур интегрирования
![]() =4
– окружность с радиусом 4 и центром в
начале координат (рис. 2).
=4
– окружность с радиусом 4 и центром в
начале координат (рис. 2).
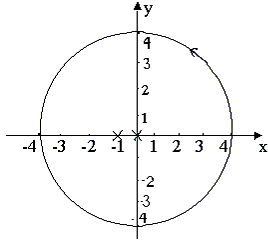
Рис. 2
F(z)
имеет две
особые изолированные точки (на рис. 2
они обозначены крестами). В примере 2
было установлено, что х1=0
– устранимая особая точка и resf(0)=0,
а
![]() – простой полюс с вычетом
– простой полюс с вычетом![]() .
.
По теореме Коши о вычетах интеграл будет равен
![]() .●
.●
Пример 5.
Вычислить
![]()
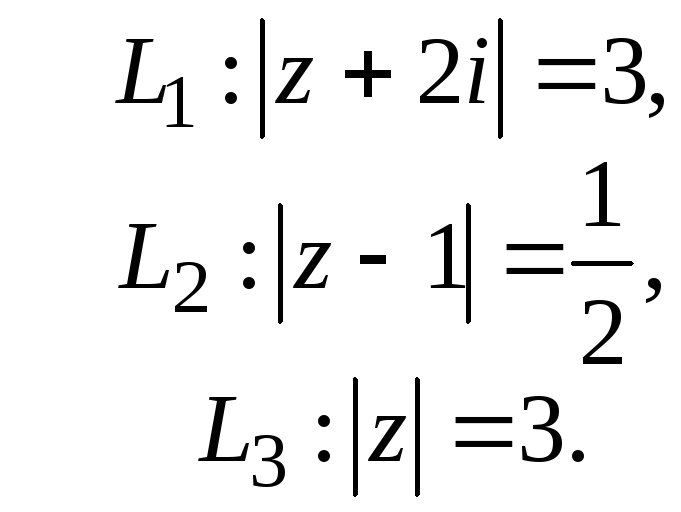
○Контуры
интегрирования изображены на рис. 3. В
Примере 3 определенно, что подынтегральная
функция имеет три особые изолированные
точки z1=0,
z2=2i,
![]() .
При этом z1=0
полюс третьего порядка, вычет в точке
z1
.
При этом z1=0
полюс третьего порядка, вычет в точке
z1
![]() .Z2=2i
– полюс
второго порядка,
.Z2=2i
– полюс
второго порядка,
![]()
![]() – полюс второго
порядка,
– полюс второго
порядка,
![]() В области ограниченнойL1-
окружностью радиуса 3 центром в точке
01
(0;-2i)
– находятся
две изолированные точки
z1=0
и
z3=-2i,
т.е.
В области ограниченнойL1-
окружностью радиуса 3 центром в точке
01
(0;-2i)
– находятся
две изолированные точки
z1=0
и
z3=-2i,
т.е.
![]() .
.
В области ограниченной
L2
, функция регулярна, следовательно, по
интегральной теореме Коши
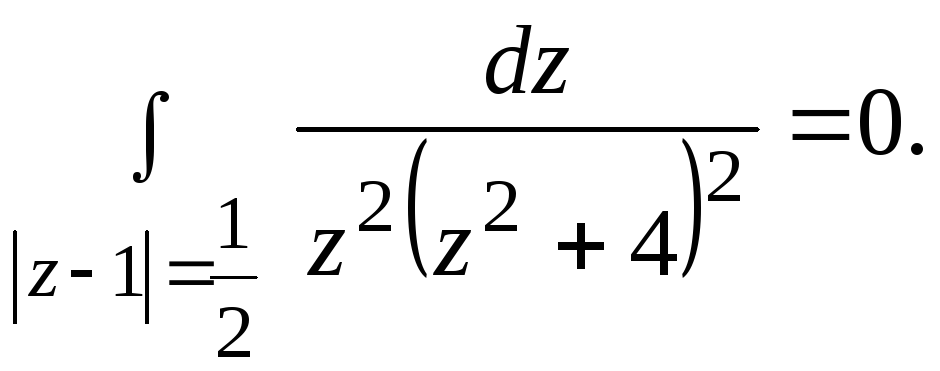
В третью область, ограниченную окружностью радиусом с центром в начале координат входят все три особые точки, поэтому
![]() ●
●
Р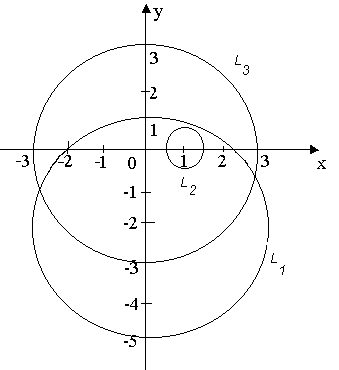 ис.
6.
ис.
6.
![]() ,
,![]() .
.
Задание 8
Определение кратчайшего пути на графе и построение минимального
остовного дерева.
Цель работы
Научиться применять алгоритм Дейкстры для определения кратчайшего пути на графах и алгоритм ближайшего соседа для построения остовного дерева.
Основные теоретические положения
Подробно изложены в разделе 3.1 (см. с.56-59).
Задание 9
Построение различных видов ДНФ для булевых функций.
Цель работы
Овладеть навыками применения метода Квайна для построения сокращенных ДНФ.
Основные теоретические положения
Подробное изложение методов см. в разделе 3.2 (с.66-72).
4.2. Методические указания к выполнению лабораторных работ
Лабораторная работа 1
Интерполяция функций с равноотстоящими узлами
методом Ньютона
1. Цель работы
Нахождение аналитического выражения функции, заданной таблицей, используя первую интерполяционную формулу Ньютона.
2. Основные теоретические положения
Материал по этой теме приведён в разделе 3 (с.19 – 22) и разделе 4 (с.84 – 87).
Здесь следует добавить, что для проверки правильности вычислений конечных разностей удобно использовать их свойство: сумма чисел в каждом столбце разностей равна разности крайних членов предыдущего столбца. Сумма всех разностей первого порядка определяется следующим образом:
![]() (1)
(1)
Например, для n = 5: ( y1 + y2 + y3 + y4 + y5) – (y0 + y1 + y2 + y3 + y4) = y5 - y0.
Аналогично, для разностей других порядков будем иметь:
![]() (2)
(2)
