
- •Кафедра информатики математика ч.2 Численные методы, теория функций комплексного переменного, дискретная математика
- •1. Информация о дисциплине
- •1.2. Содержание дисциплины и виды учебной работы3
- •Раздел 1. Численные методы (59 часов)
- •Тематический план дисциплины
- •Тематический план дисциплины
- •2.3. Структурно-логическая схема дисциплины
- •3.2. Опорный конспект
- •Раздел 1. Численные методы
- •1.1. Обработка результатов измерений и погрешности вычислений
- •Вопросы для самопроверки по теме 1.1
- •1.2. Интерполяция и численное дифференцирование
- •Вопросы для самопроверки по теме 1.2
- •1.3. Численное интегрирование
- •Вопросы для самопроверки по теме 1.3
- •1.4. Приближение функций
- •Вопросы для самопроверки по теме 1.4
- •1.5. Многомерные задачи
- •1.6. Численные методы алгебры
- •Вопросы для самопроверки по теме 1.6
- •1.7. Решение систем нелинейных уравнений и задач оптимизации
- •1.8. Численные методы решения обыкновенных дифференциальных уравнений
- •Вопросы для самопроверки по теме 1.8
- •Раздел 2. Теория функций комплексного переменного
- •2.1. Комплексные числа и действия над ними
- •Вопросы для самопроверки по теме 2.1
- •2.2. Функции комплексного переменного (фкп). Условия Коши-Римана
- •Вопросы для самопроверки по теме 2.2
- •2.3. Элементарные функции и конформные отображения
- •2.4. Представление регулярных функций интегралами
- •2.5. Представление регулярных функций рядами
- •2.6. Вычеты функций и их применение
- •Раздел 3. Дискретная математика
- •3.1. Элементы теории графов
- •3.2. Формальные языки и дискретные автоматы
- •Ответ: 101001 110100. Табл.(**)
- •3.3. Элементы алгебры логики
- •Вопросы для самопроверки по теме 3.3
- •3.4. Учебное пособие
- •Раздел 4. Блок контроля освоения дисциплины
- •4.1. Методические указания к выполнению контрольных работ Контрольные работы №1 и №2
- •Варианты индивидуальных заданий
- •Контрольная работа №1 Задание 1
- •1. Цель работы
- •2. Основные теоретические положения
- •Задание 2
- •1. Цель работы
- •Задание 3
- •2.6. Метод Симпсона
- •Задание 4
- •Контрольная работа №2 Задание 5
- •Задание 6
- •Задание 7
- •Вычет в полюсе порядка m вычисляется по формуле
- •По теореме Коши о вычетах интеграл будет равен
- •Задание 8
- •Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
- •3. Порядок выполнения работы
- •2.1. Отделение корней Графический метод отделения корней
- •Решение.
- •Аналитический метод отделения корней
- •Другие методы отделения корней
- •Метод касательных (Ньютона)
- •3. Порядок выполнения работы
- •Лабораторная работа 3
- •Решение.
- •3. Порядок выполнения работы
- •Лабораторная работа 4
- •1. Цель работы
- •2. Основные теоретические положения
- •2.1. Метод прямоугольников
- •2.2. Метод трапеций
- •2.3. Метод парабол (Симпсона)
- •3. Порядок выполнения работы
- •3. Порядок выполнения работы
- •4.3. Блок текущего контроля
- •4.3.1. Репетиционный тест по разделу 1
- •4.3.2. Репетиционный тест по разделу 2
- •4.3.3. Репетиционный тест по разделу 3
- •Ответы:
- •2. Изобразить в виде графа структуру заданного языка и построить совокупность слов, порождаемых грамматикой данного языка: Алфавит . Правила грамматики:.
- •4. Построить сднф, сокращённую и минимальную днф булевой функции, заданной таблицей. Изобразить контактные схемы для исходной, сокращённой и минимальной днф.
- •4.5. Блок итогового контроля
- •4.5.1. Вопросы к зачёту
- •Глоссарий (краткий словарь основных терминов и положений)
- •Содержание
- •Раздел 1. Численные методы ………………………………… 15
2.6. Вычеты функций и их применение
Изучаемые вопросы: Теорема Коши о вычетах; Вычисление вычетов; Вычет в бесконечно удалённой точке; Приложение вычетов к вычислению интегралов.
2.6.1. Теорема Коши о вычетах
Пусть
![]() – изолированная особая точка функции
– изолированная особая точка функции![]() .
В окрестности этой точки
.
В окрестности этой точки![]() может быть представлена рядом Лорана
может быть представлена рядом Лорана
 . (1)
. (1)
Коэффициент
![]() в разложении (1) называетсявычетом
функции
в разложении (1) называетсявычетом
функции
![]() в изолированной особой точке
в изолированной особой точке![]() .
Он обозначается как
.
Он обозначается как
![]() . (2)
. (2)
Теорема Коши.
Если
![]() регулярна в области
регулярна в области![]() всюду, за исключением внутренних точек
всюду, за исключением внутренних точек![]() ,
то интеграл от функции
,
то интеграл от функции![]() ,
взятый по контуру области
,
взятый по контуру области![]() в положительном направлении, равен
произведению
в положительном направлении, равен
произведению![]() на сумму вычетов
на сумму вычетов![]() в точках
в точках![]() :
:
 . (3)
. (3)
○ Исключим точки
![]() ,
окружив их достаточно малыми окрестностями
с границами
,
окружив их достаточно малыми окрестностями
с границами![]() (см. рисунок).
(см. рисунок).
В оставшейся области
оставшейся области![]() (она закрашена серым)
(она закрашена серым)![]() удовлетворяет всем условиям интегральной
теоремы Коши, следовательно,
удовлетворяет всем условиям интегральной
теоремы Коши, следовательно,
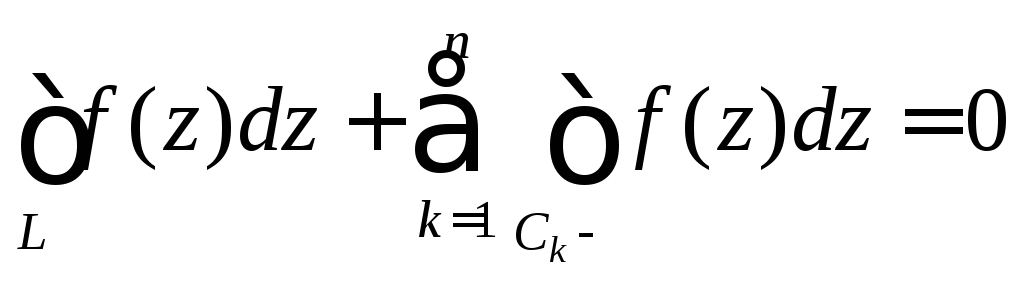 (4)
(4)
(здесь у контуров
![]() поставлен минус, т.к. обход окружностей
осуществляется в отрицательном
направлении – область
поставлен минус, т.к. обход окружностей
осуществляется в отрицательном
направлении – область![]() остаётся справа).
остаётся справа).
Но в окрестности
![]() ряд Лорана для
ряд Лорана для![]() :
:
 , (5)
, (5)
и, интегрируя почленно, получаем:
 .
.
В этом интеграле
все члены, кроме содержащего
![]() ,
равны нулю (см. п.2.4.4), а
,
равны нулю (см. п.2.4.4), а
 .
(6)
.
(6)
Изменив в (4) направление обхода, с учётом (6.) получим (3). ●
2.6.2. Вычисление вычетов
1. Рассмотрим
вычисление вычета в полюсе первого
порядка (простой полюс). Пусть в окрестности
![]() имеет место разложение
имеет место разложение
 . (7)
. (7)
Умножим обе части
этого равенства на
![]() :
:
![]() . (8)
. (8)
Устремим
![]() ,
тогда переходя к пределу, получаем
,
тогда переходя к пределу, получаем
![]() . (9)
. (9)
Выражению (9) можно
придать другой вид, если представить
 ,
где
,
где![]() – регулярные в
– регулярные в![]() функции, причём
функции, причём![]() ,
а
,
а![]() имеет простой корень. Тогда
имеет простой корень. Тогда и, по правилу Лопиталя
и, по правилу Лопиталя

 . (10)
. (10)
2. Пусть теперь
![]() – полюс порядка
– полюс порядка![]() ,
т.е. ряд Лорана функции
,
т.е. ряд Лорана функции![]() :
:
 . (11)
. (11)
![]() .
Умножим обе части этого равенства на
.
Умножим обе части этого равенства на
![]() и
продифференцируем по
и
продифференцируем по![]()
![]() раз:
раз:
![]() и устремим
и устремим
![]()
![]()
 ,
(12)
,
(12)
откуда, по аналогии с предыдущим пунктом,
 . (13)
. (13)
Пример 1.
□ Найти вычеты
 в изолированных особых точках.
в изолированных особых точках.
□ Полюсы функции
![]() расположены в точках, в которых знаменатель
дроби обращается в нуль, т.е. их можно
найти, решив уравнения
расположены в точках, в которых знаменатель
дроби обращается в нуль, т.е. их можно
найти, решив уравнения![]() и
и![]() .
Корни второго уравнения:
.
Корни второго уравнения:![]() – простые полюсы, а корень первого
уравнения
– простые полюсы, а корень первого
уравнения![]() – полюс второго порядка (он равен степени
разности
– полюс второго порядка (он равен степени
разности![]() ).
По формуле (6.9 из Учебного пособия)
находим:
).
По формуле (6.9 из Учебного пособия)
находим:

Аналогично, найдём,
что
![]()
![]() .
В полюсе второго порядка по (13)
.
В полюсе второго порядка по (13)
 .
■
.
■
2.6.3. Вычет в бесконечно удалённой точке
Пусть в окрестности
бесконечно удалённой точки
![]() функция
функция![]() представима рядом Лорана
представима рядом Лорана
![]() .
(14)
.
(14)![]()
Вычетом в
бесконечно удалённой точке
называется взятый с противоположным
знаком коэффициент при минус первой
степени
![]() в разложении (14):
в разложении (14):
![]() . (15)
. (15)
Пример
2. Найти
вычет в бесконечности функции
![]() .
.
□ Разложение
![]() в степенной ряд
в степенной ряд справедливо при любом
справедливо при любом![]() .
Тогда
.
Тогда .
■
.
■
Теорема.
Если
![]() имеет конечное число особых точек, то
сумма вычетов её, включая вычет в
бесконечно удалённой точке, равна нулю,
т.е.
имеет конечное число особых точек, то
сумма вычетов её, включая вычет в
бесконечно удалённой точке, равна нулю,
т.е.
 . (16)
. (16)
2.6.4. Приложение вычетов к вычислению интегралов
Если
![]() регулярна в односвязной области
регулярна в односвязной области![]() ,
то по теореме Коши интеграл от неё по
любому замкнутому контуру в
,
то по теореме Коши интеграл от неё по
любому замкнутому контуру в![]() равен нулю:
равен нулю:![]() .
.
Основная теорема
о вычетах:
если
![]() непрерывна на границе
непрерывна на границе![]() области
области![]() ,
за исключением конечного числа особых
точек
,
за исключением конечного числа особых
точек![]() ,
то
,
то
 . (17)
. (17)
Для вычисления этого интеграла необходимо:
Определить контур интегрирования и сделать его рисунок.
Найти особые точки подынтегральной функции, которые находятся внутри контура интегрирования, и вычислить вычеты в них, определив тип этих точек.
Используя основную теорему о вычетах, найти численное значение интеграла.
Пример 1.
Найти несобственный интеграл
 (
(![]() – вещественная переменная).
– вещественная переменная).
□ Рассмотрим
интеграл от ФКП
 ,
где
,
где![]() – комплексная переменная,
– комплексная переменная,![]() – отрезок вещественной оси,
– отрезок вещественной оси,![]() – полуокружность радиуса
– полуокружность радиуса![]() .
Вычислим
.
Вычислим![]() с помощью вычетов.
с помощью вычетов.
 Подынтегральная
функция
Подынтегральная
функция имеет полюсы второго порядка в точках
имеет полюсы второго порядка в точках![]() .
Пусть
.
Пусть![]() достаточно велико, так что
достаточно велико, так что![]() попадает внутрь контура (см. рисунок).
Тогда для полюса второго порядка, который
изображен на рисунке
попадает внутрь контура (см. рисунок).
Тогда для полюса второго порядка, который
изображен на рисунке

Следовательно,
 .
С другой стороны,
.
С другой стороны, ,
а последний интеграл
,
а последний интеграл![]() ,
и, значит,
,
и, значит,
![]() .
■
.
■
Вопросы для самопроверки по теме 2.6
Какой коэффициент ряда Лорана называется вычетом функции
 ?
?Сформулируйте теорему Коши о вычетах.
Напишите формулы для вычисления вычетов в полюсе первого порядка, полюсе порядка
 и в БУТ.
и в БУТ.Чему равна сумма вычетов функции
 ,
имеющей конечное число особых точек?
,
имеющей конечное число особых точек?
Все шесть тем этого раздела подробно описаны в Учебном пособии, которое Вам предстоит изучить. В результате Вы сможете решить задачи контрольной работы, варианты которой, в соответствии с вашим шифром, содержатся в разделе 4.
