2.5. Представление регулярных функций рядами

Изучаемые вопросы: Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса о равномерной сходимости. Степенные ряды. Теорема Абеля. Ряд Тэйлора. Разложение элементарных функций в степенные ряды. Ряд Лорана. Изолированные особые точки. Разложение в ряд Лорана в окрестности бесконечно удалённой точки.

2.5.1. Функциональные ряды

Пусть в области определены ФКП. Выражение

(1)

называется функциональным рядом. Ряд называется сходящимся в точке , если существует конечный предел частичной суммы ряда

, (2)

где , а сам пределназываетсясуммой ряда.

Это означает, что такое число, что для всех номеров

. (3)

Номер зависит, в общем, оти, но если (3) выполняется, начиная с, независимо от положения точкив области, то ряд (1) называетсяравномерно сходящимся в этой области.

Существует простой признак равномерной сходимости: если ряд (1) мажорируется (или усиливается) в области сходящимся положительным числовым рядом

, (4)

т.е. для всех и, то ряд (1) сходится равномерно в.

При рассмотрении функциональных рядов возникают два основных вопроса: а) какова область сходимости, и б) какими свойствами обладает в этой области сумма ряда. Для решения вопроса а) используются признаки сходимости (Даламбера, абсолютной сходимости, и т.д.), а для решения вопроса б) – следующие теоремы:

Теорема 1. Если члены функционального ряда (1) непрерывны в и ряд сходится равномерно, то сумма ряда– функция, непрерывная в.

Теорема 2. Если члены функционального ряда (1) непрерывны в и ряд сходится равномерно, то сумму рядаможно интегрировать почленно вдоль любой кривой, т.е.

. (5)

Теорема 3. (Вейерштрасса). Если члены ряда (1) являются регулярными функциями в области и он сходится равномерно в любой замкнутой областик сумме, то эта сумма также регулярна в, и её производные можно получить почленным дифференцированием ряда (1):

. (6)

_{Ряд, стоящий справа в (6) равномерно сходится в области .}

_{2.5.2. Ряд Тэйлора}

Степенным рядом с центром в точке называется ряд

. (7)

Числа– коэффициенты ряда (7).

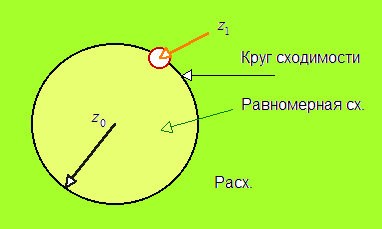
Теорема Абеля. Если степенной ряд (7) сходится в точке , то онсходится абсолютно в круге радиуса с центром в точке, причём, в любом замкнутом круге меньшего радиуса с тем же центром его сходимость равномерна. Если же он расходится в точке, то он расходится во внешности круга радиусас центром в. (см. рисунок).

На основании теоремы Абеля для любого степенного ряда доказывается существование радиуса сходимости .

Возможны три случая:

1. если , то ряд (7) сходится только в центре, т.е. в точке;

2. если , то ряд (7) сходится при любом;

3. если , то он сходится в кругеи расходится вне его. Круг

(8)

называется кругом сходимости.

Во многих случаях радиус сходимости можно найти по признаку Даламбера:

Если существует предел , то. (9)

Члены степенного ряда (7) суть регулярные функции. По теореме Абеля, внутри круга сходимости этот ряд сходится равномерно, значит, по теореме 1, сумма его регулярна внутри круга сходимости. Справедливо и обратное утверждение. Тогда можно доказать следующую теорему.

Теорема. Пусть регулярна в круге радиусас центром в. Тогда внутри этого круга её можно представить степенным рядом

=. (10)

_{При этом коэффициенты ряда выражаются формулой Тэйлора}

. (11)

Подставив (11) в (10), получим разложение в ряд Тэйлора:

. (12)

Т.о., любая , регулярная внутри круга, представима в точках этого круга в виде суммы степенного ряда и разложение это единственно.

Функция, представимая в круге степенным рядом, называется аналитической. Для ФКП аналитичность равносильна регулярности.

Примеры вычисления ряда Тэйлора для некоторых элементарных функций Вы найдёте в Учебном пособии.

2.5.3. Ряд Лорана (РЛ)

Естественным обобщением степенного ряда является ряд Лорана. Это выражение вида

, (13)

т.е. этот ряд содержит отрицательные и неотрицательные степени и есть обобщение формулы (7). Части его называются соответственноглавной и регулярной, или правильной. Коротко его можно записать в виде .

Ряд Лорана считается сходящимся, если одновременно сходятся его главная и регулярная части. Регулярная его часть – это обычный степенной ряд, и пусть его радиус сходимости , т.е. она сходится в круге

. (14)

В главной части сделаем замену , тогда получим степенной ряд

(15)

и пусть он сходится в круге . Сделаем обратную замену, найдём, что главная часть РЛ сходится во внешности круга радиусас центром в:

, (16)

и если , то область сходимости РЛ (13) – это кольцо (см. рисунок).

. (17)

Т.е. если РЛ сходится, то его область сходимости – концентрическое круговое кольцо.

Сумма РЛ есть регулярная функция внутри кольца сходимости.

Справедливо и обратное: функция регулярная в кольце может быть разложена в РЛ.

Частным случаем является : кольцо – это круг с исключённым центром. Точкав этом случае являетсяособой, в ней не определена и имеет разрыв. Оказывается, можно установить соответствие между структурой РЛ и типом особенности функции в особой точке.

2.5.4. Изолированные особые точки ФКП

Точка называетсяизолированной особой точкой функции , еслирегулярна в некотором кругес исключённым центром и нерегулярна в самой точке.

Рассмотрим виды изолированных точек:

а) называетсяустранимой особой точкой (ОТ) функции , если существует конечный предел. Для того, чтобыбыла устранимой ОТ, необходимо и достаточно, чтобы РЛв окрестностине содержал отрицательных степеней, т.е. имел бы вид

РЛ.

Пример. □имеет устранимую ОТ в. В самом деле, 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000, а предел.■

б) особая точка называетсяполюсом функции , если.

Для того, чтобы точка была полюсом, необходимо и достаточно, чтобы главная часть РЛвсодержала конечное число членов:

РЛ

(). (18)

Пусть имеет место (18). Умножим обе части его на :

. (19)

_{Здесь в знаменателе стоит степенной ряд – регулярная функция с} коэффициентом , следовательно, дробь есть также некая регулярная функция , тогда

–регулярна в точке и имеет в ней корень кратностиза счёт первого множителя. Поэтомупорядком полюса функцииназывается кратность корняфункции, и он равен максимальной степени разностив главной части ряда Лорана.

в) точка называется существенно особой точкой функции , еслине существует.

Для того, чтобы точка была существенно особой, необходимо и достаточно, чтобы РЛв окрестностисодержал бесконечное число членов с отрицательными степенями.

2.5.5. Разложение в РЛ в окрестности бесконечно удалённой точки

Ранее (п.2.1), указывалось, что называется внешность круга с центром в начале координат, т.е. она представляет собой кольцо с бесконечным внешним радиусом. Функция, которая регулярна в такой области, должна раскладываться в ней в РЛ по степеням. В этом случае также возможны три вида особенностей и, соответственно, три случая разложения:

а) , (20)

т.е., РЛ в не содержит положительных степеней. Тогдаимеет вустранимую особенность. Можно считать, что в этом случаерегулярна в окрестности бесконечно удалённой точки.

б) , (21)

т.е. РЛ содержит конечное число членов с положительными степенями. Тогда бесконечно удалённая точка является полюсом и .

в) РЛ содержит бесконечное число членов с положительными степенями. Тогда бесконечно удалённая точка является существенно особой для.

Заметим, что при разложении в ряд Лорана в окрестности бесконечно удалённой точки смысл и название частей ряда противоположны тем, что имеют место при разложении в окрестности особой точки.

Вопросы для самопроверки по теме 2.5

1. Что называется функциональным рядом и чему равна его сумма?

2. В каком случае ряд называется равномерно сходящимся?

3. Напишите выражение для степенного ряда с центром в точке .

4. Пусть степенной ряд сходится в точке , а центр его лежит в точке. Нарисуйте круг сходимости этого ряда и укажите область расходимости.

5. Напишите формулу Тэйлора.

6. Как называются различные части ряда Лорана?

7. Можно ли функцию, регулярную в круге разложить в ряд Лорана?

8. Какие виды изолированных особых точек Вы знаете?