Тест № 2

1. Дана симплекс-таблица начального базисного решения.

базис	значения	x1	x2	s1	s2
s1	56	8	14	1	0
s2	25	6	5	0	1
z	0	-3	-5	0	0

Переменную x₂ вводим в базис. Найдите переменную, выходящую из базиса.

А. s₁ В. s₂ С. Нет переменных, выходящих из базиса

9. Определяет ли данная таблица оптимальный план?

базис	значения	x1	x2	s1	s2
x2	4	0,571	1	0,0714	0
s2	5	3,143	0	-0,357	1
z	20	-0,143	0	0,3571	0

23. Да; В. Нет.

10. В заданной симплекс-таблице найти переменную, которую нужно вводить в базис

базис	значения	x1	x2	s1	s2
x2	4	0,571	1	0,0714	0
s2	5	3,143	0	-0,357	1
z	20	-0,143	0	0,3571	0

24. s₁; В. x₁; С. Нет таких переменных.

11. Найдите оптимальный план выпуска первой продукции

базис	значения	x1	x2	s1	s2
x2	3,091	0	1	0,136	-0,182
x1	1,591	1	0	-0,114	0,3182
z	20,227	0	0	0,3409	0,0455

25. 1,591; В. 3,091; С. 1

12. Найдите максимальной значение выручки по таблице вопроса 4.

26. 4,682; В. 24,909; С. 20,227.

13. Найдите оптимальную теневую цену второго ресурса по таблице вопроса 4.

27. 0,3182; В. 0,3409; С. 0,0455.

14. На сколько изменится выручка при увеличении второго ресурса на 1 (таблица вопроса 4)?

28. 3,091; В. 0,0455; С. 0,3182.

15. На сколько изменится оптимальный план выпуска первой продукции при увеличении первого ресурса на 1 (таблица вопроса 4)?

29. 0,136; В. -0,114; С. 1.

16. На сколько изменится оптимальный план выпуска второй продукции при увеличении первого ресурса на 1?

30. 0,136; В. -0,114; С. 1

Тест № 3

1. Для игры с матрицей . Найти выигрыш игрокаI, если он выбирает строку 3, а игрок II выбирает столбец 2.

31. 8; В. -12; С. 12.

17. Для игры с матрицей, данной в вопросе 1 найти выигрыш игрока II в ситуации (2,4).

32. 9; В. -8; С. -12.

18. Для игры с матрицей, данной в вопросе 1. найти (max)i (min)j a(i,j)

33. 12; В. 10; С. 9.

19. Для игры с матрицей, данной в вопросе 1 найти (min)j (max)i a(i,j)

34. 10; В. 12; С. 14.

20. Для игры с матрицей, данной в вопросе 1 найти ситуацию равновесия в чистых стратегиях

35. (4,1); В. (1,4); С. (2,4).

21. Для игры с матрицей, данной в вопросе 1 найти, чему равно значение этой матричной игры

36. 12; В. 14; С. 10.

Тест № 4

1. Может ли матрица 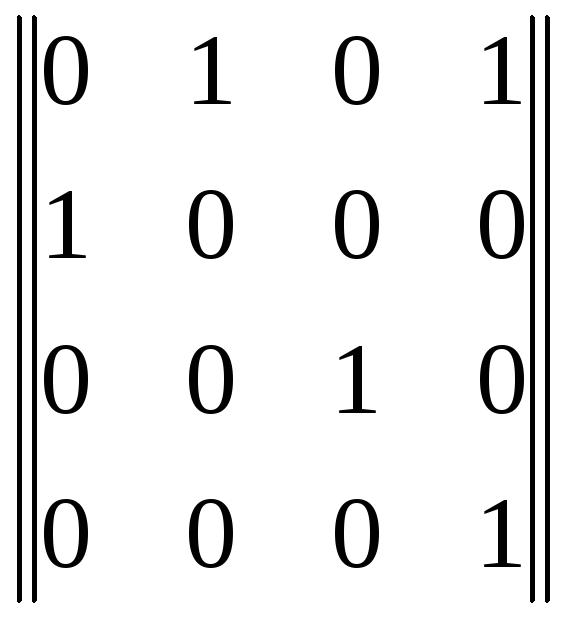служить матрицей назначений

1. Да; В. Нет.

22. Вычислить стоимость работ для матрицы назначений если стоимость работ задается матрицей

37. 11; В. 7; С. 28.

23. Является x₁ = 100, x₂ = 230 допустимым решением задачи квадратич-ного программирования Min

при ограничениях x₁ + x₂ ≥ 300, x₁ ≥ 0, x₂ ≥ 0.

38. Да; В. Нет.

24. Запишите матрицу D целевой функции квадратичного программирования Minx₂

39. B. C.