
- •Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Кафедра теоретической и прикладной механики
- •1. Информация о дисциплине
- •1.1 Предисловие
- •- Операции со скоростями и ускорениями при сложном движении точки;
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1.Содержание дисциплины по гос
- •1.2.2. Объём дисциплины и виды учебной работы
- •1.2.3. Перечень видов практических занятий и контроля:
- •2. Рабочие учебные материалы
- •Раздел 1. Кинематика
- •Раздел 2. Динамика и элементы статики
- •2.2. Тематический план дисциплины
- •2.3. Структурно-логическая схема дисциплины
- •2.4. Практический блок
- •2.4.1. Практические занятия
- •2.5. Временной график изучения дисциплины
- •2.6. Балльно-рейтинговая система оценки знаний
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект по дисциплине
- •Раздел 1. Кинематика
- •1.1. Кинематика точки
- •1.1.1. Способы задания движения точки
- •1.1.2. Скорость точки
- •1.1.3. Ускорение точки при векторном и координатном способах задания движения
- •1.1.4. Ускорение точки при естественном способе задания движения
- •1.2. Простейшие движения твердого тела
- •1.2.1. Поступательное движение твердого тела
- •1.2.2. Вращение твердого тела вокруг неподвижной оси
- •1.2.3. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси
- •1.2.4. Векторное представление скорости точки вращающегося твёрдого тела
- •1.3. Сложное движение точки
- •1.3.1. Относительное, переносное и абсолютное движения точки
- •1.3.2. Относительные, переносные и абсолютные скорости и ускорения точки
- •1.3.3. Теоремы сложения скоростей
- •1.3.4. Теорема сложения ускорений (теорема Кориолиса)
- •1.3.5. Ускорение Кориолиса
- •1.4. Плоское движение твёрдого тела
- •1.4.1. Плоское движение твёрдого тела и движение
- •1.4.2. Теорема сложения скоростей при плоском движении
- •1.4.3. Теорема о проекциях скоростей двух точек плоской фигуры
- •1.5. Движение твёрдого тела вокруг неподвижной точки и движение свободного твёрдого тела
- •1.5.1. Движение твердого тела вокруг неподвижной точки
- •Или сферическое движение; углы Эйлера, уравнения движения
- •1.5.2. Скорости точек тела. Мгновенная ось вращения
- •1.5.3.Общий случай движения свободного твердого тела
- •1.6. Сложное движение твёрдого тела
- •1.6.1.Сложение поступательных движений
- •1.6.2. Сложение вращений вокруг пересекающихся осей
- •1.6.3. Сложение вращательных движений вокруг параллельных осей
- •Раздел 2. Динамика и элементы статики
- •2.1. Введение в динамику и статику
- •2.1.1. Предмет динамики и статики. Основные понятия
- •2.1.2. Свободные и несвободные тела. Связи и реакции связей
- •2.1.3. Законы механики Галилея – Ньютона
- •2.1.4. Момент силы относительно оси
- •2.1.5 Трение покоя и трение скольжения
- •2.1.6. Пара сил и ее свойства
- •2.1.7. Пара трения качения
- •2.2. Статика твёрдого тела
- •2.2.1. Условия и уравнения равновесия произвольной системы сил
- •2.2.2. Уравнения равновесия плоской системы сил
- •2.2.3. Равновесие системы твёрдых тел
- •2.3. Динамика материальной точки
- •2.3.1. Основное уравнение динамики материальной точки в декартовых и естественных координатах
- •2.3.2. Две основные задачи динамики материальной точки
- •2.3.3. Динамика относительного движения материальной точки
- •2.3.4. Свободные гармонические колебания материальной точки
- •2.3.5. Свободные затухающие колебания материальной точки
- •2.3.6. Вынужденные колебания материальной точки
- •2.4. Введение в динамику механической системы
- •2.4.1. Механическая система. Классификация сил. Дифференциаль- ные уравнения движения. Свойства внутренних сил
- •2.4.2. Масса системы. Центр масс системы
- •2.5. Теоремы о движении центра масс и об изменении количества движения механической системы
- •2.5.1.Теорема о движении центра масс системы
- •2.5.2. Количество движения материальной точки и механической системы. Импульс силы
- •2.5.3. Теорема об изменении количества движения системы
- •2.6. Теорема об изменении главного момента количества
- •2.6.1. Момент количества движения материальной точки относительно центра и оси
- •2.6.2. Кинетический момент системы относительно центра и оси
- •2.6.3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
- •2.6.4. Теоремы об изменении кинетического момента системы
- •2.6.5. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
- •2.7. Работа и энергия
- •2.7.1. Кинетическая энергия материальной точки и механической системы
- •2.7.2. Кинетическая энергия твердого тела
- •2.7.3. Работа и мощность силы
- •2.7.4. Работа силы тяжести и силы упругости
- •2.7.5. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси
- •2.7.6. Теорема об изменении кинетической энергии
- •2.7.7. Теорема об изменении кинетической энергии системы
- •2.7.8. Понятие о силовом поле
- •2.7.9. Закон сохранения механической энергии
- •2.8. Метод кинетостатики (принцип Даламбера)
- •2.8.1. Принцип Даламбера для материальной точки и механической системы
- •2.8.2. Приведение сил инерции твёрдого тела к данному центру
- •2.Вращательное движение вокруг неподвижной оси.
- •3.3. Глоссарий (краткий словарь терминов)
- •3.4. Методические указания и примеры решения задач
- •Алгоритм решения задач на применение теоремы об изменении кинетической энергии механической системы
- •4. Блок контроля освоения дисциплины
- •4.1. Задания на контрольные работы и методические указания к их выполнению
- •4.1.1. Общие указания
- •4.1.2. Указания к выполнению контрольной работы №1
- •4.1.3. Указания к выполнению контрольной работы № 2
- •4.2. Текущий контроль
- •4.2.1. Тренировочные тесты текущего контроля
- •4.2.2. Тренировочные тесты рубежного контроля
- •4.3. Итоговый контроль. Вопросы к экзамену
2.7.6. Теорема об изменении кинетической энергии
материальной точки
Изменение кинетической энергии материальной точки на некотором ее перемещении равно сумме работ всех сил, приложенных к точке, на этом же перемещении.
Доказательство. Движение материальной
точки массой![]() относительно инерциальной системы
отсчета описывается основным уравнением
динамики:
относительно инерциальной системы
отсчета описывается основным уравнением
динамики:![]() ,
,
где
![]() - равнодействующая всех сил, действующих
на точку.
- равнодействующая всех сил, действующих
на точку.
Умножим обе части этого уравнения на
![]() ,
получим:
,
получим:
![]() или
или![]() .
.
Учитывая, что
![]() ,
имеем:
,
имеем:
![]() или
или![]() , (2.7.21)
, (2.7.21)
где
![]() - сумма элементарных работ всех сил на
элементарном перемещении
- сумма элементарных работ всех сил на
элементарном перемещении![]() точки.
точки.
Интегрируя левую и правую части этого уравнения в соответствующих пределах, получим:
![]() или
или![]() .
(2.7.22) Здесь
.
(2.7.22) Здесь![]() и
и![]() - значения скорости точки в ее начальном
- значения скорости точки в ее начальном![]() и конечном
и конечном![]() положениях,
положениях,![]() - работа всех действующих на точку сил
на перемещении
- работа всех действующих на точку сил
на перемещении![]() .Теорема доказанав дифференциальной
(2.7.21) и интегральной (2.7.22) формах.
.Теорема доказанав дифференциальной
(2.7.21) и интегральной (2.7.22) формах.
2.7.7. Теорема об изменении кинетической энергии системы
Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ всех действующих на систему внешних и внутренних сил на этом перемещении.
Доказанная выше теорема справедлива
для любой точки механической системы.
Применяя уравнение (2.7.21) для некоторой
![]() -й
точки системы, получим:
-й
точки системы, получим:![]() .
.
Составляя такие уравнения для всех точек системы и складывая их почленно, получим:
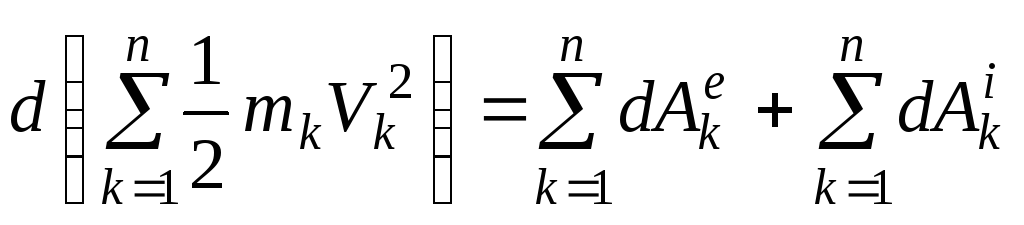
или
![]() .
(2.7.23)
.
(2.7.23)
Здесь
![]() -
кинетическая энергия всех точек системы.
-
кинетическая энергия всех точек системы.
Интегрируя выражение (2.7.23) в соответствующих пределах получим:
![]()
![]() .
(2.7.24)
.
(2.7.24)
Теорема доказанав дифференциальной (2.7.23) и интегральной (2.7.24) формах.
В отличие от ранее рассмотренных общих теорем динамики системы, позволяющих в какой-то мере не учитывать действие внутренних сил, последняя теорема требует учета их действия. Однако, если рассматриваемая механическая система является неизменяемой(в частности, если рассматриваетсятвердое тело), то сумма внутренних сил в этом случае равна нулю и в уравнениях (2.7.23) и (2.7.24) в правых частях остаются лишь первые слагаемые.
2.7.8. Понятие о силовом поле
Область пространства, в которой на помещённую туда материальную точку действует сила, зависящая от координаты этой точки в рассматриваемой системе отсчёта и времени, называется силовым полем. Силовые поля делятся на однородные и неоднородные, стационарные и нестационарные, потенциальные и непотенциальные Примерами силовых полей являются поля силы тяжести, силы тяготения , силы упругости, а также электрические и магнитные поля.
Если работа сил поля при движении в нем материальной точки не зависит от ее траектории, а также закона движения по этой траектории из одного положения в другое, то такое поле называется потенциальным силовым полем, а действующие в нем силы называютсяпотенциальными.
 Примерами потенциальных сил являются
силы тяжести и силы упругости.
Примерами потенциальных сил являются
силы тяжести и силы упругости.
Если же работа силы, действующей на точку, зависит от ее траектории, то такая сила называется непотенциальной.
К ним относятся, например, силы трения и силы сопротивления среды.
Для точки или системы, находящихся в
потенциальном поле, вводится понятие
потенциальной энергии
![]() ,
как величины, численно равной работе
по перемещению точки силами поля из
данного положения в так называемое
нулевое положение. Это положение, в
котором потенциальная энергия принимается
равной нулю, выбирается произвольно.
,
как величины, численно равной работе
по перемещению точки силами поля из
данного положения в так называемое
нулевое положение. Это положение, в
котором потенциальная энергия принимается
равной нулю, выбирается произвольно.
Поскольку работа в потенциальном поле
зависит только от начального и конечного
положений, то после выбора нулевого
положения и переноса в эту точку начала
координат, потенциальная энергия будет
однозначной функцией координат
![]() каждой точки системы в данном положении.
Таким образом:
каждой точки системы в данном положении.
Таким образом:
![]() .
(2.7.25)
.
(2.7.25)
Чтобы определить потенциальную энергию
системы в некотором положении
![]() ,
надо вычислить работу сил поля, действующих
на точки системы при перемещении ее из
этого положения в нулевое, то есть
,
надо вычислить работу сил поля, действующих
на точки системы при перемещении ее из
этого положения в нулевое, то есть
![]() .
.![]() (2.7.26)
(2.7.26)
Здесь
![]() - работа сил поля, приложенных к
- работа сил поля, приложенных к![]() -й
точке на данном перемещении
-й
точке на данном перемещении![]() .
.
Пусть некоторое твердое тело массы m
находится в поле силы тяжести (рис.
2.7.6). Поскольку равнодействующая![]() сил тяжести приложена к центру масс
тела, то следует определять его
потенциальную энергию по положению
центра масс. Выберем систему отсчета
сил тяжести приложена к центру масс
тела, то следует определять его
потенциальную энергию по положению
центра масс. Выберем систему отсчета![]() с осью
с осью![]() ,
направленной верти-кально вверх.
Обозначим
,
направленной верти-кально вверх.
Обозначим![]() - координаты центра масс
- координаты центра масс![]() тела в положе-нии
тела в положе-нии![]() .
За нулевое выберем положение тела, в
котором его центр масс совпа-дает с
любой точкой горизонтальной плоскости
.
За нулевое выберем положение тела, в
котором его центр масс совпа-дает с
любой точкой горизонтальной плоскости![]() .
Этому положению и соответствует нулевой
уровень потенциальной энергии, т.е.
.
Этому положению и соответствует нулевой
уровень потенциальной энергии, т.е.![]() .
.
В соответствии с формулой (2.7.16) при
перемещении тела из положения
![]() в нулевое положение работа силы тяжести
равна
в нулевое положение работа силы тяжести
равна
![]() .
.
Поэтому потенциальная энергия твердого тела в поле силы тяжести равна
![]() .
(2.7.27)
.
(2.7.27)
Теперь рассмотрим материальную точку,
на которую действует сила упругости
пружины. За нулевое положение примем
положение точки, в котором деформация
пружины равна нулю. Тогда в соответствии
с формулой (2.7.17) при перемещении точки
из данного положения
![]() в нулевое сила упругости совершит работу
в нулевое сила упругости совершит работу![]() ,
,
где
![]() - коэффициент жесткости пружины, а
- коэффициент жесткости пружины, а![]() - удлинение или сжатие пружины в данном
положении.
- удлинение или сжатие пружины в данном
положении.
Поэтому потенциальная энергия точки в поле силы упругости равна
![]() .
(2.7.28)
.
(2.7.28)
Выразим работу потенциальных сил через
потенциальную энергию. Для этого
рассмотрим некоторые положения системы
![]() и
и![]() .
Так как работа сил потенциального поля
не зависит от вида траекторий точек
системы, то работа на перемещении системы
из положения
.
Так как работа сил потенциального поля
не зависит от вида траекторий точек
системы, то работа на перемещении системы
из положения![]() в нулевое положение будет равна работе
на перемещении
в нулевое положение будет равна работе
на перемещении![]() через положение
через положение![]() ,
что выразится следующим образом:
,
что выразится следующим образом:
![]() ,
,
где
![]() и
и![]() - суммы работ сил поля на перемещениях
системы из положений
- суммы работ сил поля на перемещениях
системы из положений![]() и
и![]() в нулевое положение,
в нулевое положение,![]() - сумма работ сил поля на перемещении
системы из положения
- сумма работ сил поля на перемещении
системы из положения![]() в положение
в положение![]() .
.
Учитывая формулу (2.7.26), получим:
![]() .
(2.7.29)
.
(2.7.29)
Таким образом, работа потенциальных
сил равна разности значений потенциальной
энергии в начальном и конечном положениях
системы. При перемещении по замкнутому
контуру работа этих сил обращается в
нуль, так как в этом случае![]() .
.
