
- •Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Кафедра теоретической и прикладной механики
- •1. Информация о дисциплине
- •1.1 Предисловие
- •- Операции со скоростями и ускорениями при сложном движении точки;
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1.Содержание дисциплины по гос
- •1.2.2. Объём дисциплины и виды учебной работы
- •1.2.3. Перечень видов практических занятий и контроля:
- •2. Рабочие учебные материалы
- •Раздел 1. Кинематика
- •Раздел 2. Динамика и элементы статики
- •2.2. Тематический план дисциплины
- •2.3. Структурно-логическая схема дисциплины
- •2.4. Практический блок
- •2.4.1. Практические занятия
- •2.5. Временной график изучения дисциплины
- •2.6. Балльно-рейтинговая система оценки знаний
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект по дисциплине
- •Раздел 1. Кинематика
- •1.1. Кинематика точки
- •1.1.1. Способы задания движения точки
- •1.1.2. Скорость точки
- •1.1.3. Ускорение точки при векторном и координатном способах задания движения
- •1.1.4. Ускорение точки при естественном способе задания движения
- •1.2. Простейшие движения твердого тела
- •1.2.1. Поступательное движение твердого тела
- •1.2.2. Вращение твердого тела вокруг неподвижной оси
- •1.2.3. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси
- •1.2.4. Векторное представление скорости точки вращающегося твёрдого тела
- •1.3. Сложное движение точки
- •1.3.1. Относительное, переносное и абсолютное движения точки
- •1.3.2. Относительные, переносные и абсолютные скорости и ускорения точки
- •1.3.3. Теоремы сложения скоростей
- •1.3.4. Теорема сложения ускорений (теорема Кориолиса)
- •1.3.5. Ускорение Кориолиса
- •1.4. Плоское движение твёрдого тела
- •1.4.1. Плоское движение твёрдого тела и движение
- •1.4.2. Теорема сложения скоростей при плоском движении
- •1.4.3. Теорема о проекциях скоростей двух точек плоской фигуры
- •1.5. Движение твёрдого тела вокруг неподвижной точки и движение свободного твёрдого тела
- •1.5.1. Движение твердого тела вокруг неподвижной точки
- •Или сферическое движение; углы Эйлера, уравнения движения
- •1.5.2. Скорости точек тела. Мгновенная ось вращения
- •1.5.3.Общий случай движения свободного твердого тела
- •1.6. Сложное движение твёрдого тела
- •1.6.1.Сложение поступательных движений
- •1.6.2. Сложение вращений вокруг пересекающихся осей
- •1.6.3. Сложение вращательных движений вокруг параллельных осей
- •Раздел 2. Динамика и элементы статики
- •2.1. Введение в динамику и статику
- •2.1.1. Предмет динамики и статики. Основные понятия
- •2.1.2. Свободные и несвободные тела. Связи и реакции связей
- •2.1.3. Законы механики Галилея – Ньютона
- •2.1.4. Момент силы относительно оси
- •2.1.5 Трение покоя и трение скольжения
- •2.1.6. Пара сил и ее свойства
- •2.1.7. Пара трения качения
- •2.2. Статика твёрдого тела
- •2.2.1. Условия и уравнения равновесия произвольной системы сил
- •2.2.2. Уравнения равновесия плоской системы сил
- •2.2.3. Равновесие системы твёрдых тел
- •2.3. Динамика материальной точки
- •2.3.1. Основное уравнение динамики материальной точки в декартовых и естественных координатах
- •2.3.2. Две основные задачи динамики материальной точки
- •2.3.3. Динамика относительного движения материальной точки
- •2.3.4. Свободные гармонические колебания материальной точки
- •2.3.5. Свободные затухающие колебания материальной точки
- •2.3.6. Вынужденные колебания материальной точки
- •2.4. Введение в динамику механической системы
- •2.4.1. Механическая система. Классификация сил. Дифференциаль- ные уравнения движения. Свойства внутренних сил
- •2.4.2. Масса системы. Центр масс системы
- •2.5. Теоремы о движении центра масс и об изменении количества движения механической системы
- •2.5.1.Теорема о движении центра масс системы
- •2.5.2. Количество движения материальной точки и механической системы. Импульс силы
- •2.5.3. Теорема об изменении количества движения системы
- •2.6. Теорема об изменении главного момента количества
- •2.6.1. Момент количества движения материальной точки относительно центра и оси
- •2.6.2. Кинетический момент системы относительно центра и оси
- •2.6.3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
- •2.6.4. Теоремы об изменении кинетического момента системы
- •2.6.5. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
- •2.7. Работа и энергия
- •2.7.1. Кинетическая энергия материальной точки и механической системы
- •2.7.2. Кинетическая энергия твердого тела
- •2.7.3. Работа и мощность силы
- •2.7.4. Работа силы тяжести и силы упругости
- •2.7.5. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси
- •2.7.6. Теорема об изменении кинетической энергии
- •2.7.7. Теорема об изменении кинетической энергии системы
- •2.7.8. Понятие о силовом поле
- •2.7.9. Закон сохранения механической энергии
- •2.8. Метод кинетостатики (принцип Даламбера)
- •2.8.1. Принцип Даламбера для материальной точки и механической системы
- •2.8.2. Приведение сил инерции твёрдого тела к данному центру
- •2.Вращательное движение вокруг неподвижной оси.
- •3.3. Глоссарий (краткий словарь терминов)
- •3.4. Методические указания и примеры решения задач
- •Алгоритм решения задач на применение теоремы об изменении кинетической энергии механической системы
- •4. Блок контроля освоения дисциплины
- •4.1. Задания на контрольные работы и методические указания к их выполнению
- •4.1.1. Общие указания
- •4.1.2. Указания к выполнению контрольной работы №1
- •4.1.3. Указания к выполнению контрольной работы № 2
- •4.2. Текущий контроль
- •4.2.1. Тренировочные тесты текущего контроля
- •4.2.2. Тренировочные тесты рубежного контроля
- •4.3. Итоговый контроль. Вопросы к экзамену
2.7.4. Работа силы тяжести и силы упругости
Определим работу силы тяжести точки
![]() на некотором ее перемещении
на некотором ее перемещении![]() (рис. 2.7.3). Считая это перемещение малым
по сравнению с радиусом Земли, можно
допустить, что модуль и направление
силы тяжести точки
(рис. 2.7.3). Считая это перемещение малым
по сравнению с радиусом Земли, можно
допустить, что модуль и направление
силы тяжести точки![]() являются постоянными. Выберем систему
отсчета
являются постоянными. Выберем систему
отсчета![]() ,
направив ось
,
направив ось![]() вверх по вертикали.
вверх по вертикали.
Используя формулу (2.7.9) и учитывая, что проекции силы тяжести на оси координат равны
![]() ,
,
получим выражение для элементарной
работы силы тяжести:
![]() .
.
Работа силы тяжести точки на конечном
перемещении
![]() будет определяться определенным
интегралом:
будет определяться определенным
интегралом: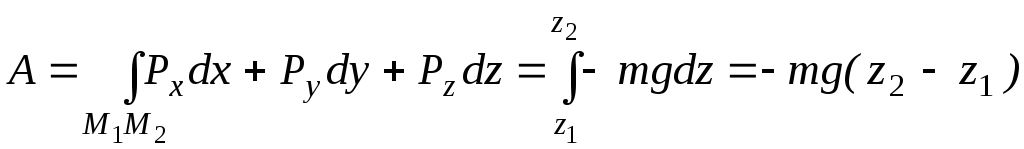 .
(2.7.14)
.
(2.7.14)
Если
![]() (точка опускается), то работа силы тяжести
положительна, если
(точка опускается), то работа силы тяжести
положительна, если![]() (точка поднимается), то работа отрицательна.
(точка поднимается), то работа отрицательна.
Из формулы (2.7.14) следует, что работа силы
тяжести не зависит от формы траектории
и закона движения точки по траектории.
На замкнутой траектории эта работа
равна нулю, так как тогда
![]() .
.
О пределим
теперь работу силыупругости
пределим
теперь работу силыупругости
![]() ,
действующую на материальную точку
,
действующую на материальную точку![]() (рис 2.7.4). Эта сила всегда направлена к
положению равновесия
(рис 2.7.4). Эта сила всегда направлена к
положению равновесия![]() ,
по модулю пропорциональна расстоянию
,
по модулю пропорциональна расстоянию![]() точки от этого положения и определяется
выражением:
точки от этого положения и определяется
выражением:
![]() ,
(2.7.15)
,
(2.7.15)
где
![]() - радиус-вектор точки
- радиус-вектор точки![]() относительно точки
относительно точки![]() ,
,![]() - коэффициент жесткости упругого
элемента, например пружины.
- коэффициент жесткости упругого
элемента, например пружины.
Используя формулы (2.7.8), (2.7.15) и правила дифференцирования, находим элементарную работу силы упругости
![]() .
(2.7.16)
.
(2.7.16)
Интегрируя равенство (2.7.16), получаем работу силы упругости на коннечном перемещении её точки приложения
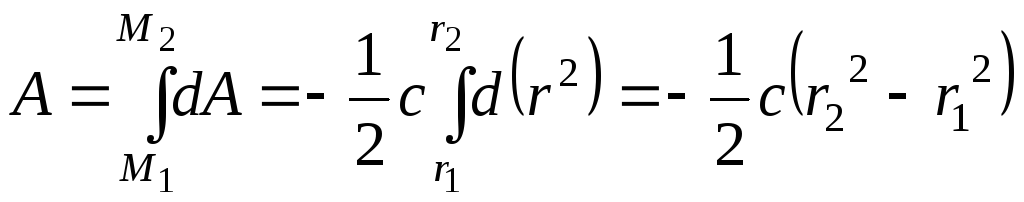 .
(2.7.17)
.
(2.7.17)
Таким образом, работа силы упругости
пропорциональна разности квадратов
начального и конечного отклонений точки
от положения равновесия. Подобно работе
силы тяжести, работа силы упругости не
зависит от вида траектории и закона
движения точки по траектории. На замкнутой
траектории эта работа равна нулю, так
как тогда
![]() .
.
Если работа производится пружиной, то
величина
![]() в формуле (2.7.17) заменяется величиной
в формуле (2.7.17) заменяется величиной![]() деформации пружины в начальном и конечном
положениях.
деформации пружины в начальном и конечном
положениях.
2.7.5. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси
Рассмотрим твердое тело, вращающееся
с угловой скоростью
![]() вокруг неподвижной оси
вокруг неподвижной оси![]() под действием системы внешних сил
под действием системы внешних сил![]() (рис.2.7.5). Пусть одна из сил
(рис.2.7.5). Пусть одна из сил![]() приложена в точке тела
приложена в точке тела![]() ,
положение которой определяется
радиус-вектором
,
положение которой определяется
радиус-вектором![]() .
.
Из кинематики известно, что скорость
точки вращающегося тела может быть
выражена формулой
![]() .
Используя правило векторной алгебры,
найдем мощность приложенных к телу сил
.
Используя правило векторной алгебры,
найдем мощность приложенных к телу сил![]() ,
,
и ли
ли![]() ,
(2.7.18)
,
(2.7.18)
где
![]() - проекция главного момента
- проекция главного момента![]() системы приложенных к телу сил на ось
системы приложенных к телу сил на ось![]() ,
то есть главный момент системы сил
относительно оси
,
то есть главный момент системы сил
относительно оси![]() .
Величина
.
Величина![]() носит названиевращающего момента.
Таким образом, мощность системы сил,
приложенных к вращающемуся вокруг
неподвижной оси твердому телу, равна
произведению угловой скорости тела и
вращающего момента.
носит названиевращающего момента.
Таким образом, мощность системы сил,
приложенных к вращающемуся вокруг
неподвижной оси твердому телу, равна
произведению угловой скорости тела и
вращающего момента.
Определим теперь работу этой системы
сил. Предположим, что под действием
приложенных сил тело повернулось за
время
![]() на угол
на угол![]() ,
при этом точка тела
,
при этом точка тела![]() перешла из положения
перешла из положения![]() в положение
в положение![]() .
Применяя полученные выше формулы,
найдем:
.
Применяя полученные выше формулы,
найдем:
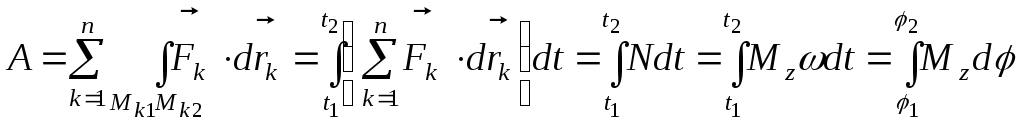 .
.
Итак, работа равна
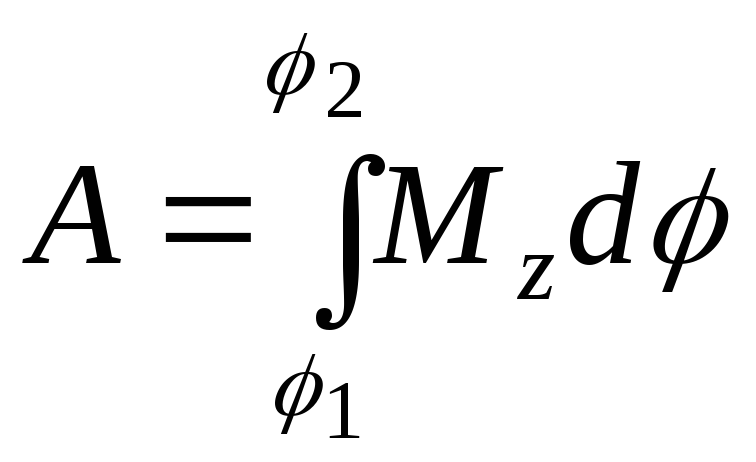 .
(2.7.19)
.
(2.7.19)
Если вращающий момент постоянен
![]() ,
то работа равна произведению момента
на угол
,
то работа равна произведению момента
на угол![]() поворота тела, то есть
поворота тела, то есть
![]() .
(2.7.20)
.
(2.7.20)
