2.4. Введение в динамику механической системы

В этой теме раскрываются: понятие – механическая система, а также свойства, уравнения и формулы, характеризующие её состояние: 1. свойство внутренних сил системы 2. уравнения движения точек механической системы 3. радиус- вектор центра масс механической системы 4. координаты центра масс механической системы

2.4.1. Механическая система. Классификация сил. Дифференциаль- ные уравнения движения. Свойства внутренних сил

В предыдущих темах изучалась динамика одной материальной точки. Практически же в технике чаще встречаются задачи, когда движение одной материальной точки нельзя изучать изолированно от движения других точек или тел. Это приводит к необходимости перейти от динамики точки к изучению динамики механической системы.

Механической системойназывается совокупность материальных то-чек или тел, движения которых взаимосвязаны.Механической системой будут являться Солнечная планетная система, какой-либо механизм или машина.

Силы, приложенные к точкам системы можно разделить на внешниеивнутренние.Внешниминазываются силы, действующие на систему извне.Внутренниминазываются силы взаимодействия между материальными точкамисамой системы. Отметим, что в состав внешних и внутренних сил могут входить какактивные силы, так иреакции связей. В дальнейшем условимся обозначать внешнюю силу , а внутреннюю - .

С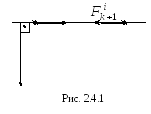войства внутренних сил.Рассмотрим механическую систему, сос-тоящую изматериальных точек. Силы взаимодействия в каждой паре точек в соответствии с третьим законом Ньютона равны по модулю и противоположны по направлению. На рис. 2.4.1 изображены две произвольно выбранные точкии, и силы их взаимодействияи, равные по модулю и противоположно направленные вдоль одной и той же прямой. Следовательно, моменты этих сил относительно произвольного центраО равны по модулю и противоположны по направлению. В силу сказанного, сумма сил взаимодействия и сумма моментов этих сил соответственно равны нулю:

. Распространяя эти суждения на все точки системы, устанавливаем, что главный вектор и главный момент внутренних сил материальной системы равны нулю:. (2.4.1)

Равенства (2.4.1) выражают свойства внутренних сил. Применяя принцип освобождаемости от связей (см. тему 2.1), заменим связи их реакциями. Обозначим через и равнодействующие соответственно внешних и внутренних сил, приложенных к точке системы с номером. С учетом уравнения (2.3.1) опишем движение этой системы следующимиуравнениями:

, (2.4.2)

где и- масса и ускорение-й точки системы. В проекциях на оси инерциальной декартовой системы координат имеем:

;;, . (2.4.3)

Уравнения (2.4.3) представляют собой систему дифференциальных уравнений движения материальных точек механической системы.

Решение задачи динамики механической системы путем интегрирования системы дифференциальных уравнений (2.4.3) практически нереализуемо, поскольку внутренние силы и входящие в число внешних сил реакции связей заранее неизвестны, а числоточек системы может быть достаточно велико.

В связи с этим в теоретической механике разработаны методы, позволяю-щие в какой-то степени обойти указанные трудности. При этом в рассмотрение вводятся векторные и скалярные величины, характеризующие движение механической системы в целом и называемые мерами движениясистемы. К числу таких мер относятся количество движения, момент количества движения (кинетический момент) и кинетическая энергия механической системы.