1.4. Плоское движение твёрдого тела

В этой теме рассмотрено сложное движение твёрдого тела, при котором все его точки перемещаются по различным криволинейным плоским траекториям. Плоское движение тела раскладывается на поступательное и вращательное. Вам предстоит изучить способы определения скоростей и ускорений точек тела, а также его угловой скорости и углового ускорения. Эти способы основываются на следующих понятиях и теоремах: 1.– уравнения движения плоской фигуры 2. -теорема сложения скоростей при плоском движении 3.скорость точкиВво вращении плоской фигуры относительно полюсаА 4. свойство скорости точки плоской фигуры во вращении вокруг полюса 5. VB│АВ=VA│AB(или ) - теорема о проекциях скоростей двух точек плоской фигуры на ось, проходящую через эти точки 6. (или) - свойство мгновенного центра скоростей плоской фигуры 7. - теорема сложения ускорений при плоском движении

1.4.1. Плоское движение твёрдого тела и движение

плоской фигуры в её плоскости

Определение. Движение твёрдого тела, при котором все его точки перемещаются в плоскостях параллельных некоторой неподвижной плоскости П, называется плоским или плоскопараллельным.

Многие части (звенья) современных машин и механизмов совершают плоское. Например, движение шатуна в двигателе автомобиля, прямолинейное качение колеса. Пусть твёрдое тело совершает плоское движение относительно неподвижной плоскости П. Расположим плоскостьПтак, чтобы она пересекла движущееся тело (рис.1.4.1). В сечении получим плоскую фигуру(S), которая скользит по неподвижной плоскости. Проведём мысленно через тело перпендикулярBCк плоскости .Он пересечёт фигуру(S) в точкеА.При плоском движении тела прямаяВСбудет перемещаться параллельно своемуначальному положению, то есть поступательно. Все точки прямойВС, включая точкуА, движутся одинаково, т.е. траектории, скорости и ускорения всех точек прямойВСодинаковые.

Отсюда следует, что при изучении плоского движения твёрдого тела можно 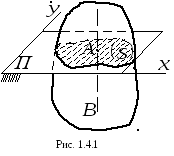ограничиться изучением движения плоской фигуры(S)в плоскости(рис. 1.4.2). Положение плоской фигуры на плоскостивполне определяется положением любых её двух точекАиВ или положением отрезкаАВ. Принимая точкуАза полюс, свяжем с точкойА поступательно движущуюся систему координатAx₁y₁, так что при движении фигурыAx₁║ Ox, аAy₁ ║ Oy . Тогда положение отрезкаАВ, а следовательно и фигуры(S), в плоскостиопределится положениемполюса А иуглом, называемом углом поворота фигуры(S) вокруг полюсаА. Координатыx_A , y_A полюса Аи уголявляются непрерывными функциями времени:

x_A = x_A(t), y_A = y_A(t), φ = φ(t). (1.4.1)

Функции (1.4.1) называются уравнениями плоского движения твёрдого тела или плоской фигуры.

Из уравнений (1.4.1) видно, что движение плоской фигуры можно мысленно представить как сложное, состоящее из поступательного движения подвижной системы координат вместе с полюсомАивращательного вокруг этого полюса.

Угол поворота , угловая скорость и угловое ускорение плоской фигуры не зависят от выбора полюса. Действительно, если в качестве полюса выбрать любую другую точку фигуры(S), то подвижную систему координат необходимо поместить в эту точку путём параллельного переноса, при этом угол между отрезкомAB и осьюOxостанется прежним, равным.