2) Решение симплекс-методом

Приведём задачу к каноническому виду, введя дополнительные переменные. Расширенная система задачи имеет вид:

4x₁ + х₂ + х₃ = 400

6х₁ + 5х₂ + х₄ = 745

2х₁ + 6х₂ + х₅ = 660, где х_i ≥ 0, i =1,2,3,4,5.

Линейную функцию представим в виде f =16х₁+ 22х₂ + 0∙х₃ + 0∙х₄ + 0∙х₅ или f - 16х₁ -22х₂ - 0∙х₃ - 0∙х₄ - 0∙х₅ = 0

Заполним первую симплекс-таблицу:

Таблица 1

Базис	Свободный член	Переменные						Оценочное отношение
		х1	х2	х3	х4	х5
х3	400	4	1	1	0	0	400
х4	745	6	5	0	1	0	745/5=149
х5	660	2	6	0	0	1	660/6=110
f	0	-16	-22	0	0	0

В последней строке имеются отрицательные коэффициенты, значит, план для максимума не является оптимальным. Перейдём ко второй симплекс-таблице.

- Наибольший по модулю отрицательный коэффициент последней строки (-22) определяет разрешающий столбец 2.

- Находим оценочные отношения и min{400; 149; 110}= 110, третья строка является разрешающей. На пересечении разрешающей строки и столбца стоит разрешающий элемент а₂₂ = 6.

- Новый базис - переменные х₃, х₄, х₂

- Во второй строке все элементы получаются делением на разрешающий элемент а₂₂ = 6. Остальные клетки заполняем по правилу прямоугольника. Например, а₁₁ = 4 – (1∙2)/6 = 11/3.

Получим вторую симплекс-таблицу:

Таблица 2

Базис	Свободный член	Переменные						Оценочное отношение
		х1	х2	х3	х4	х5
х3	290		0	1	0		79,09
х4	195		0	0	1		45
х2	110		1	0	0		330
f	2420		0	0	0

Критерий оптимальности снова не выполняется. Теперь первый столбец разрешающий; х₁ переходит в базисные, вторая строка разрешающая, а₂₁ = – разрешающий элемент. Третья симплекс-таблица имеет вид:

Таблица 3

Базис	Свободный член	Переменные
		х1	х2	х3	х4	х5
х3	125	0	0	1
х1	45	1	0	0
х2	95	0	1	0
f	2810	0	0	0	2	2

Критерий оптимальности для максимума выполнен (все коэффициенты последней строки неотрицательны), значит оптимальное базисное решение Х=(45; 95; 125; 0; 0), то есть х₁ = 45; х₂ = 95 - план производства изделий А₁ и А₂, обеспечивающий максимальную прибыль предприятия от реализации готовой продукции:

f_max = 16∙45 + 22∙95 = 2810 (ден.ед.)

3) Двойственная задача

Исходная задача на максимизацию, и все неравенства системы ограничений имеют вид ≤ :

4х₁ +х₂ ≤ 400

6х₁ + 5х₂ ≤ 745

2х₁ + 6х₂ ≤ 660, где х₁ ≥ 0, х₂ ≥ 0

Составим расширенную матрицу системы:

4	1	400
6	5	745
2	6	660
16	22	fmax

А=

Найдём матрицу А^т, транспонированную к матрице А:

4	6	2	16
1	5	6	22
400	745	660	zmin

А^т=

Сформулируем двойственную задачу:

Найти минимум функции z = 400y₁ +745y₂ + 660y₃ при ограничениях:

4y₁ + 6y₂ + 2y₃ ≥ 16

y₁ + 5y₂ + 6y₃ ≥ 22, где y₁, y₂, y₃ ≥0

Канонический вид задачи: найти минимум функции z = 400y₁ +745y₂ + 660y₃ + 0∙y₄ + 0∙y₅ при ограничениях

4y₁ + 6y₂ + 2y₃ - y₄ = 16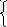

у₁ + 5у₂ + 6у₃ - у₅ = 22, где у₁, у₂, у₃, у₄, у₅≥0

На основании теоремы двойственности установим соответствие между переменными:

х₁↔ у₅, х₂↔ у₄, х₃↔ у₁, х₄↔ у₂, х₅↔ у₃

Таблица 4

х1	х2	х3	х4	х5
0	0	0	2	2
у4	у5	у1	у2	у3

Тогда оптимальное базисное решение двойственной задачи:

У=(0; 2; 2; 0; 0), откуда у₁ =0, у₂ = 2, у₃ =2.

z_min= 400∙0+745∙2 + 660∙2= 2810,

z_min = f_max= 2810 ден.ед.

Задача 2. На три базы А₁, А₂, А₃ поступил однородный груз в количестве а₁, а₂, а₃ тонн. Этот груз необходимо развезти пяти потребителям В₁, В₂, В₃, В₄, В₅, потребности которых в данном грузе составляют b₁, b₂, b₃, b₄, b₅ тонн соответственно.

Таблица 5

Пункт отправления	В1	В2	В3	В4	В5	Запасы аi (тонн)
А1	2	10	15	14	4	350
А2	3	7	12	5	8	350
А3	21	18	6	13	16	300
Потребности, bi (тонн)	180	220	230	270	100	1000

Требуется спланировать перевозки так, чтобы их общая стоимость была минимальной.

Решение

Опорный план задачи составим методом наименьших затрат.

min c_ij = c₁₁ = 2, a₁ = 350, b₁ =180, min{350; 180} = 180. Число 180 записываем в клетку (1;1), теперь a₁ =350-180=170, b₁ = 0.

min c_ij = c₁₅ = 4, a₁= 170, b₅ =100, min{170; 100} = 100. Число 100 записываем в клетку (1; 5), теперь a₁ =70, b₅ = 0.

min c_ij = c₂₄ = 5, a₂ =350, b₄ = 270, min{270; 350} = 270. Число 270 записываем в клетку (2; 4), теперь a₂ = 80, b₄=0.

min c_ij = c₃₃ = 6, a₃ = 300, b₃ = 230, min{300; 230} =230. Число 230 записываем в клетку (3;3), теперь a₃ = 70, b₃ = 0.

Распределяем таким образом грузы до тех пор, пока все запасы не будут исчерпаны, а все поставки не будут удовлетворены. Получим первый опорный план задачи:

Таблица 6

ui	Потребители Базы	В1			В2			В3			В4			В5			Запасы аi
0	А1	180	2	70		10	-		15	-		14	100		4	350
-3	А2	-	3	80		7	-		12	270		5	-		8	350
8	А3	-	21	70		18	230		6	-		13	-		16	300
	Потребности, bi	180			220			230			270			100			520
	vj	2			10			-2			8			4

Стоимость перевозок: f =180∙2+70∙10+100∙4+80∙7+270∙5+70∙18+230·6 = =360+700+400+560+1350+1260+1380 = 6010.

Число занятых клеток m+n-1=3+5-1=7, значит план невырожденный, поэтому решим задачу методом потенциалов.

Рассчитаем потенциалы для занятых клеток так, что u_i + v_i = c_ij

Пусть u₁ =0, тогда v₁ = c₁₁ – u₁ = 2 – 0 =2

v₂ = c₁₂ – u₁ = 10 – 0 = 10

v₅ = c₁₅ – u₁ = 4 – 0 = 4

u₂ = c₂₂ – v₂ = 7 – 10 = -3

u₃ = c₃₂ – v₂ = 18 – 10 = 8

v₃ = c₃₃ – u₃ = 6 - 8 = -2

v₄ = c₂₄ – u₂ =5 +3 = 8

Проверим выполнение условий оптимальности для незанятых клеток: u_i + v_i ≤ c_ij

(1; 3): u₁ + v₃ = 0-2 = -2 < 15

(1; 4): u₁ + v₄ = 0+8 = 8 < 14

(2; 1): u₂ + v₁ = -3+2 = -1 < 3

(2; 3): u₂ + v₃ = -3-2 = -5 <12

(2; 5): u₂ + v₅= -3+4 = 1 <8

(3; 1): u₃ + v₁ = 8+2 = 10 < 21

(3; 4): u₃ + v₄ = 8+8 = 16 > 13

(3; 5): u₃ + v₅ = 8+4= 12< 16

Условие u_i + v_i ≤ c_ij не выполняется для клетки (3; 4), поэтому план не является оптимальным. «Загрузим» клетку (3; 4), составив для неё цикл. После перемещения груза по циклу получим второй план:

Таблица 7

ui	Потребители Базы	В1			В2			В3			В4			В5			Запасы аi
0	А1	180	2	70		10	-		15	-		14	100		4	350
-3	А2	-	3	150		7	-		12	200		5	-		8	350
5	А3	-	21	-		18	230		6	70		13	-		16	300
	Потребности, bi	180			220			230			270			100			520
	vj	2			10			1			8			4

Потенциалы для занятых клеток: u_i + v_i = c_ij

Пусть u₁ =0, тогда v₁ = c₁₁ – u₁ = 2 – 0 =2

v₂ = c₁₂ – u₁ = 10 – 0 = 10

v₅ = c₁₅ – u₁ = 4 – 0 = 4

u₂ = c₂₂ – v₂ = 7 – 10 = -3

v₄ = c₂₄ – u₂ =5 +3 = 8

u₃ = c₂₄ – v₄ = 13 – 8 = 5

v₃ = c₃₃ – u₃ = 6 - 5 = 1

Рассчитаем выполнение условий оптимальности для незанятых клеток: u_i + v_i ≤ c_ij

(1; 3): u₁ + v₃ = 0+1 = 1 ≤ 15

(1; 4): u₁ + v₄ = 0+8 = 8 ≤ 14

(2; 1): u₂ + v₁ = -3+2 = -1 ≤ 3

(2; 3): u₂ + v₃ = -3+1 = -2 ≤ 12

(2; 5): u₂ + v₅= -3+4 = 1 ≤ 8

(3; 1): u₃ + v₁ =5+2 = 7 ≤ 21

(3; 4): u₃ + v₄ = 5+8 = 13 ≤ 13

(3; 5): u₃ + v₅ = 8+4= 12 ≤ 16

План является оптимальным, так как для всех незанятых клеток выполняется условие u_i + v_i ≤ c_ij . Минимальная стоимость перевозок:

f_min=180∙2+70∙10+100∙4+150∙7+200∙5+70∙13+230·6= =360+700+400+1050+1000+910+1380 = 5800.

Задача 3 Даны работы и их длительность. Построить сетевую модель, разбить по слоям вершины и дуги, найти критический путь, вычислить все резервы событий.

Работа,(i; j)	Время, tij	Работа,(i; j)	Время, tij	Работа,(i; j)	Время, tij
(0, 1)	5	(2, 6)	10	(5, 7)	7
(0, 2)	3	(3, 4)	8	(5, 8)	4
(0, 3)	4	(3, 6)	5	(6, 7)	8
(1, 2)	2	(4, 6)	7	(6, 9)	8
(1, 3)	9	(4, 7)	7	(7, 8)	10
(1, 5)	7	(4, 8)	6	(7,9)	6
(2, 5)	2	(5, 4)	9	(8, 9)	7

Решение

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ, заданного в специфической форме сети, графическое изображение которой называется сетевым графиком (графом).

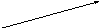
Зададим граф в виде матрицы смежности, разобьём по слоям вершины и дуги:

4

2

2

5

8

3

6

101

9

7

7

2

6

7

0

4

7

9

7

5

10

1

8

8

7

8

9

6

4

5

3

1 слой

2 слой

3 слой

4 слой

5 слой

6 слой

7 слой

8 слой

9 слой

Полный путь называется критическим, если сумма времён выполнения работ, в него входящих, самая большая среди времён всех других полных путей.

Найдём критический путь для данной задачи:

τ = t (0; 1)+ t (1; 3)+ t (3; 4)+ t (4; 6)+ t (6; 7)+ t (7; 8) + t (8; 9) =5+9+8+7+8+10+7=54.

Критический путь имеет вид: 0→1→3→4→6→7→8→9.

События 0, 1, 3, 4, 6, 7, 8, 9 и работы, входящие в критический путь, также являются критическими. Резервы критических событий равны нулю. У событий и работ, не являющихся критическими, есть некоторый резерв. Не являются критическими события 2, 5. Вычислим их резервы:

Т(5) = t(5, 4) + t(4, 6) + t(6, 7) + t(7, 8) + t(8, 9) = 9+7+8+10+7 =41;

τ*₅ = 54 – 41 = 13; τ₅ = 5+7=12; R(5)= 13 – 12 =1;

T(2)= t(2, 5) + t(5, 4) + t(4, 6) + t(6, 7) + t(7, 8) + t(8, 9) = 2+9+7+8+10+7 =43;

τ*₁ = 54 – 43 = 11; τ₄=5+2=7; R(2)= 11 – 7 = 4.