
- •Кинетика химических процессов.
- •Реакции нулевого порядка
- •A b
- •Кинетика реакций первого порядка
- •Пример решения задачи в системе MathCad
- •Кинетика реакций второго порядка
- •Пример решения задачи Всистеме MathCad
- •Линейные цепи реакций
- •Разветвленные цепи реакций
- •Кинетика процессов в открытой системе
- •Кинетика реакций ферментативного катализа
- •Кинетическая модель Михаэлиса – Ментена
- •Конкурентное ингибирование
- •Неконкурентное ингибирование
Пример решения задачи в системе MathCad
![]()

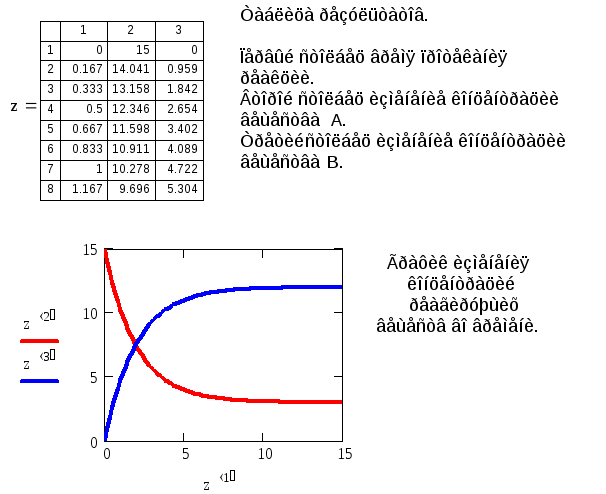
Кинетика реакций второго порядка
Реакция второго порядка имеет вид:
(![]() 5)
5)
Будем считать, что исходные концентрации реагирующих веществ (а если речь идет о модели каких-то биологических процессов – исходные численности взаимодействующих элементов системы) равны при t=0 соответственно a0иb0.Обозначимх - количество каждого из реагирующих веществ, израсходованного в течение времениt.Поскольку вещества взаимодействуют в отношении 1:1, для каждого из ниххбудет иметь одно и то же значение. Поэтому кинетическое уравнение можно записать так:
(![]() 6)
6)
Э![]() то
дифференциальное уравнение с разделяющимися
переменными. Произведя эту операцию,
получим
то
дифференциальное уравнение с разделяющимися
переменными. Произведя эту операцию,
получим
Используя алгебраическое тождество
![]()
п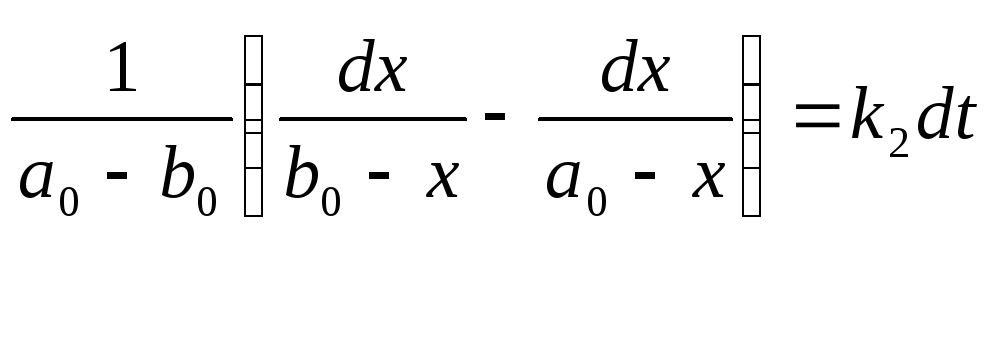 олучим
удобный для интегрирования вид уравнения
(6):
олучим
удобный для интегрирования вид уравнения
(6):
После интегрирования и нахождения постоянной интегрирования из условия при t=0,x=0 получим
![]()
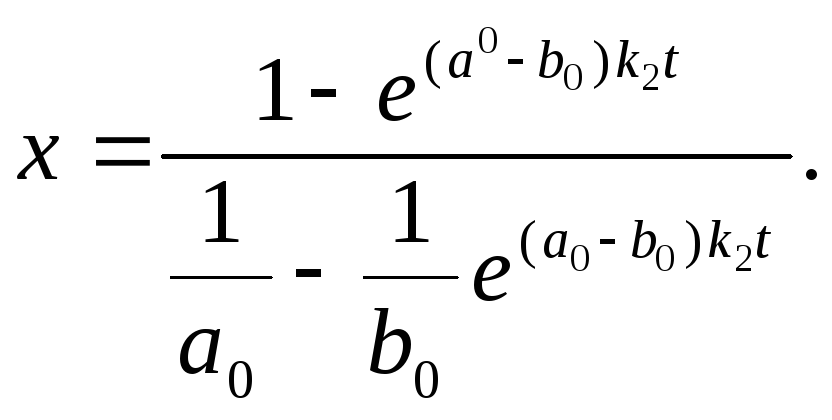
и![]() ли
ли
Легко убедиться, что при наличии большого избытка одного из реагентов, например В, так что b0по все время процесса можно считать постоянной, реакция будет протекать как реакция первого порядка b выражение длях(что соответствует количеству продукта в правой части (5)) будет иметь вид такой же, как и в предыдущем разделе. Подобная ситуация типична для биохимических процессов, где вода является одним из реагирующих веществ, поскольку в большинстве биологических систем она присутствует в избытке, так что концентрация ее всегда практически постоянна.
Р![]() ассмотрим
один пример реакции второго порядка. В
уравнении реакции первого порядка,
описывающем скорость размножения клеток
ассмотрим
один пример реакции второго порядка. В
уравнении реакции первого порядка,
описывающем скорость размножения клеток
величина α не является постоянной, так как следует учитывать, что клетки не только размножаются, но и погибают, выбывая из процесса экспоненциального роста. Поэтому Ферхюльстом и Пирлем (в 1924 г.) была предложена зависимость α от числа клеток
α = β – γN
так что кинетическое уравнение приняло вид
г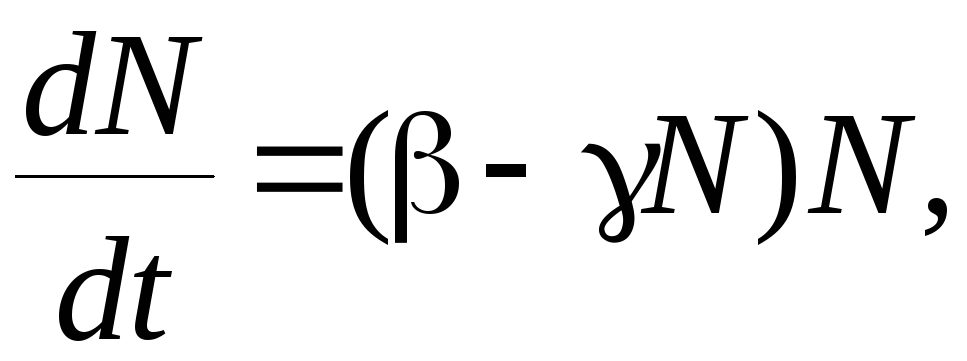 де
β и γ – константы.
де
β и γ – константы.
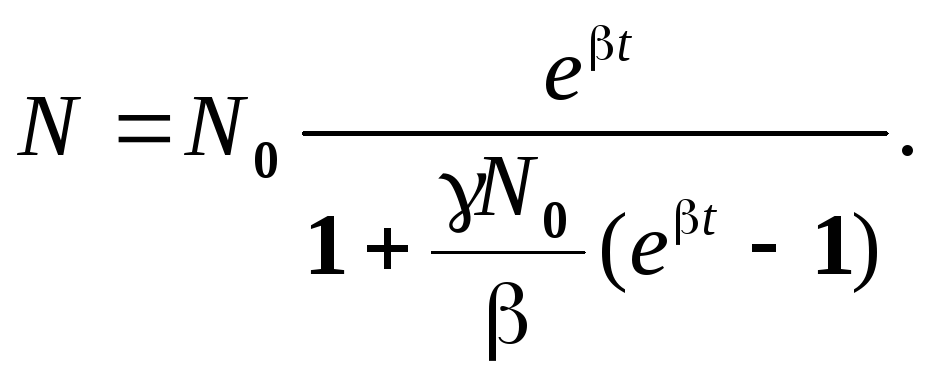 Очевидно, что это уравнение второго
порядка. Его решение имеет вид
Очевидно, что это уравнение второго
порядка. Его решение имеет вид
Пример решения задачи Всистеме MathCad

Линейные цепи реакций
М![]() ножество
метаболических процессов и процессов
более высокого уровня биологической
организации представляют цепи
последовательных превращений, которые
можно упрощенно представить в виде
трехзвенной цепи: субстрат - промежуточный
продукт – конечный продукт:
ножество
метаболических процессов и процессов
более высокого уровня биологической
организации представляют цепи
последовательных превращений, которые
можно упрощенно представить в виде
трехзвенной цепи: субстрат - промежуточный
продукт – конечный продукт:
О![]() говорим
вновь условия протекания процесса. Приt
= 0, a
= a0,
b
= c
= 0.
Система закрытая, так что а+b+с=а0
в любой момент времени. Запишем систему
уравнений:
говорим
вновь условия протекания процесса. Приt
= 0, a
= a0,
b
= c
= 0.
Система закрытая, так что а+b+с=а0
в любой момент времени. Запишем систему
уравнений:
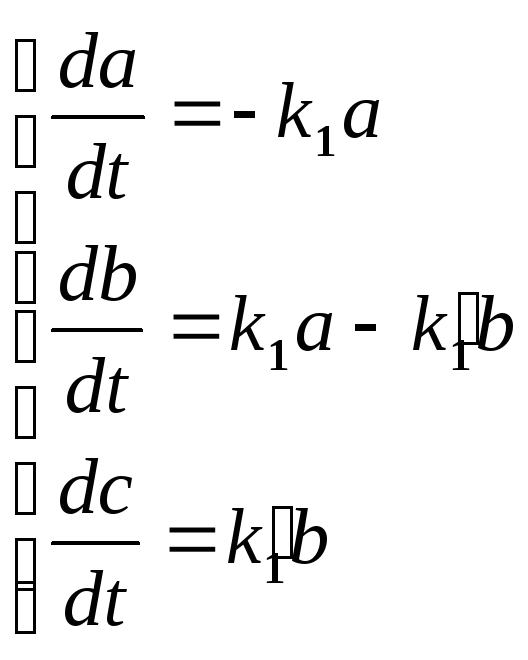
![]()
Р![]() ешение
первого из уравнений (9) можно записать
сразу:
ешение
первого из уравнений (9) можно записать
сразу:
Из условия постоянства массы вещества в системе имеем:
П![]()
![]() одставляя
это выражение в последнее из уравнении
(9), получим
одставляя
это выражение в последнее из уравнении
(9), получим
О![]()
![]() бщее
решение этого уравнения с правой частью,
отличной от нуля, как известно, складывается
из решения однородного уравнения
бщее
решение этого уравнения с правой частью,
отличной от нуля, как известно, складывается
из решения однородного уравнения
и![]() частного решения неоднородного уравнения.
Это частное решение будем искать в виде
частного решения неоднородного уравнения.
Это частное решение будем искать в виде
г![]() деR1 иR2—искомые
постоянные. Подставляя это выражение
в уравнение (10), получим
деR1 иR2—искомые
постоянные. Подставляя это выражение
в уравнение (10), получим
П![]() риравнивая
свободные членыикоэффициенты при экспонентах, найдем
риравнивая
свободные членыикоэффициенты при экспонентах, найдем
Полное решение уравнения (10) выглядит с учетом общего решения однородного уравнения так:
И![]()
![]() з
начальных условии найдем константу
интегрирования С:
з
начальных условии найдем константу
интегрирования С:
В окончательном виде решение для сзапишется:
![]()
Выражение для bнаходится без труда из условия сохранения количеств вещества. После несложных преобразовании оно приводится к виду:
![]()
Ч![]() астным
случаем трехзвенной цепи является также
последовательность превращений первого
и пулевого порядков
астным
случаем трехзвенной цепи является также
последовательность превращений первого
и пулевого порядков
В этом случае кинетические уравнения упрощаются:
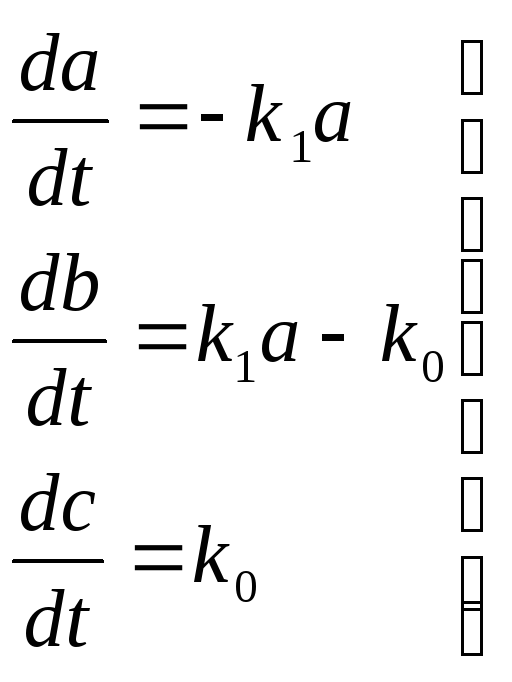
и дают такие решения (при сохранении указанных условий):
Х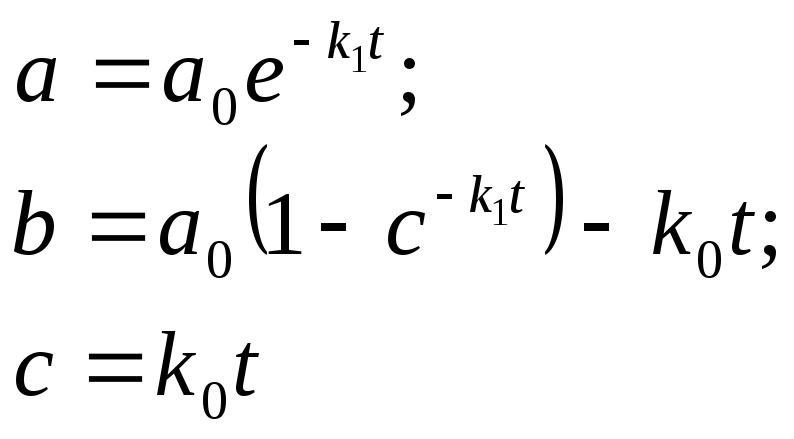 арактерными
примерами подобных цепей являются
многие ферментативные реакции при
высоких концентрациях субстрата,
некоторые стадии всасывания аминокислот,
условия размножения насекомых и др.
арактерными
примерами подобных цепей являются
многие ферментативные реакции при
высоких концентрациях субстрата,
некоторые стадии всасывания аминокислот,
условия размножения насекомых и др.
