
- •Занятие 22 второе начало термодинамики
- •Литература
- •Контрольные вопросы для подготовки к занятию
- •Краткие теоретические сведения и основные формулы
- •Термический кпд идеального цикла Карно
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Качественные задачи
- •Задачи для самостоятельного решения
Решение
Изобразим
цикл Карно на рис. 22.10,
![]() по условию.
по условию.
Мощность
![]() ,
,
где А – работа, совершенная воздухом за один цикл.
В процессе 1 - 2 рабочее тело получает тепло от нагревателя и совершает работу, так как это процесс изотермический, то
![]()
КПД цикла Карно:
![]()
отсюда
![]()
Из уравнения Пуассона можно найти отношение

но
так как
 где
где
![]()
Воздух
- смесь в основном двухатомных газов,
поэтому
![]()
Тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() Вт
= 6,2 .
Вт
= 6,2 .![]() Вт.
Вт.
Ответ: N = 6,2 . 105 Вт.
Задача 4. 6,6 г водорода расширяются изобарически до удвоения объема. Найти изменение энтропии при этом расширении. Построить график зависимости S от T.
Д ано:Решение
ано:Решение
р
Изменение
энтропии газа при переходе из одного
состояния в другое определяется только
параметрами этих состояний и не зависит
от характера процесса:
![]() .
.
т
= 6,6
![]() кг
кг
=
2
![]()
![]()
![]()
 S
- ?
S
- ?
Из
первого начала термодинамики для
изобарного процесса (р
= const)
получим количество теплоты
![]() :
:
![]() ,
,
![]() ,
,
![]()
где
![]()
Работа
![]() (это следует из уравнения состояния
идеального газа;
(это следует из уравнения состояния
идеального газа;![]() ).
).
Тогда
![]()
![]()
Интегрируя, получаем

Для изобарного процесса
![]()
Тогда
![]()
По условию
![]()
Вычислим S:
![]()
![]() .
.
Вывод:
Энтропия при изобарном расширении
водорода увеличилась
![]() ,
следовательно, процесс необратим,
самопроизвольно сжиматься газ не может.
Энтропия указывает направление процесса.
,
следовательно, процесс необратим,
самопроизвольно сжиматься газ не может.
Энтропия указывает направление процесса.

Задача 5. Найти изменение энтропии при изотермическом расширении водорода т = 6 г в пределах 105…0,5 .105 Па. Построить график зависимости S от р и S от V.
Д
 ано:
ано:
T = const
m
=
6 .![]() кг
кг
=
2 .![]()
![]()
![]() =
=
![]() Па
Па
![]() Па
Па
R
= 8,31
![]()
 S
- ?
S
- ?
Решение
Т = const.
![]()
 из
уравнения состояния имеем
из
уравнения состояния имеем
![]() тогда
тогда ;
;![]() для изотермического процесса, поэтому
для изотермического процесса, поэтому
![]()
![]() .
.
В изотермическом процессе S > 0 при расширении.
Ответ:
S
= 17,3
![]() .
.
Задача 6. Найти изменение внутренней энергии, энтропии и работы совершенной газом при переходе газа из состояния А в состояние В по пути: а) АСВ и б) по пути АDВ (рис.22.13).

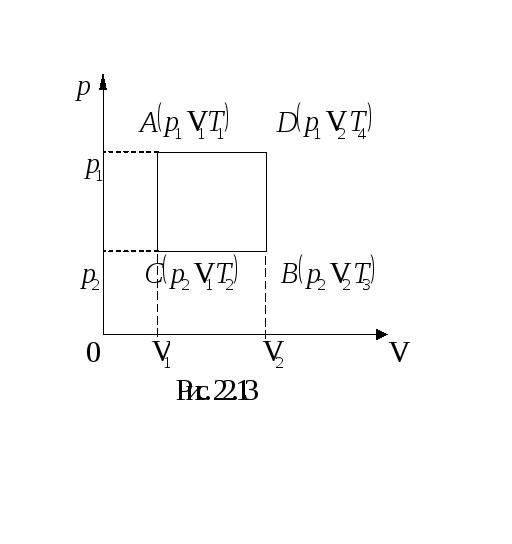 Дано:
Дано:
=
8,2
![]()
![]() =
3 л = 3 .
=
3 л = 3 .![]() м3
м3
![]() л
= 4,5 .
л
= 4,5 .![]() м3
м3
![]() =
8,2 .
=
8,2 .![]() Па
Па
![]()
 Па
Па
![]()
Решение
I. а) путь АСВ:

б) путь АDВ:

Вывод:
![]() ,
т. е. внутренняя энергия является функцией
состояния, изменение от процесса не
зависит.
,
т. е. внутренняя энергия является функцией
состояния, изменение от процесса не
зависит.
![]()
II.![]() ,
так как
,
так как![]() ,
а
,
а![]()
![]()
![]() .
.
ААСВ = 6 . 105 (4,5 . 10-3 – 3 . 10-3) = 900 Дж;
АADB = 8,2 . 105 (4,5 . 10-3 – 3 . 10-3) = 1230 Дж.
Работа
зависит от процесса
![]() .
.
III.
 ;
;

![]()
![]()
![]()
![]()
![]()
Из газовых законов получаем
![]() .
.
Тогда
![]()
![]()
то есть
![]()
Энтропия и внутренняя энергия являются функциями состояния. Их изменение не зависит от пути перехода, а зависит только от начального и конечного состояний.
Ответ:
U1
= U2
= 600 Дж, А1
= 900 Дж, А2
= 1230 Дж, S1
= S2
= = 305
![]() .
.
Качественные задачи
Задача 1. Изобразите для идеального газа графики изотермического и адиабатного процессов на диаграмме U, S (U – внутренняя энергия, S – энтропия).
Задача 2. Изобразите для идеального газа примерные графики изотермического, изохорного, изобарного и адиабатного процессов на диаграмме: 1) T, S; 2) V, S; 3) p, S. S откладывать по оси абсцисс. Графики изобразить проходящими через общую для них точку.
З адача
3.На рис.
22.14 изображены пять процессов, протекающих
с идеальным газом. Как ведет себя
внутренняя энергия газа в ходе каждого
из процессов? Как ведет себя энтропии
в ходе каждого из процессов?
адача
3.На рис.
22.14 изображены пять процессов, протекающих
с идеальным газом. Как ведет себя
внутренняя энергия газа в ходе каждого
из процессов? Как ведет себя энтропии
в ходе каждого из процессов?
Задача 4. Изобразите для идеального газа примерные графики изохорного, изобарного, изотермического и адиабатного процессов на диаграмме: 1) S, T; 2) S, V; 3) S, p. S откладывать по оси ординат. Графики имеют общую для всех исходную точку.
Задача 5. На рис. 22.15 изображен цикл Карно на диаграмме p, V для идеального газа. Какая из заштрихованных площадей больше, I или II?

Задача 6. На рис. 22.16 изображены две изоэнтропы для одной и той же массы идеального газа. Какая из энтропий больше?

Задача
7*. Идеальный
газ (с известным )
совершает круговой процесс, состоящий
из двух изотерм и двух изобар. Изотермические
процессы протекают при температурах
![]() и
и![]()
![]() изобарные – при давленияхр1
и р2
(р2
в е
раз больше, чем
р1).
Найти КПД цикла.
изобарные – при давленияхр1
и р2
(р2
в е
раз больше, чем
р1).
Найти КПД цикла.
Задача 8. Как ведет себя энтропия термодинамической системы при адиабатическом процессе?
Задача 9. Некоторое количество газа переходит из равновесного состояния 1 в равновесное состояние 2 посредством: а) обратимого адиабатного процесса; б) некоторого необратимого процесса. Начальное и конечное состояния газа для обоих процессов одинаковы. 1. Чему равно приращение энтропии газа S в обоих случаях? 2. Может ли второй процесс быть также адиабатическим?
Задача 10*. Идеальный газ совершает цикл, состоящий из двух изотерм и двух изохор. 1) Как ведет себя: а) внутренняя энергия; б) энтропия на различных участках цикла? 2) На каких участках: а) совершенная газом работа А; б) полученное газом тепло Q больше (меньше) нуля?
Задача 11*. Идеальный газ совершает цикл, состоящий из двух адиабат и двух изобар. 1. Как ведет себя: а) внутренняя энергия; б) энтропия на различных участках цикла? 2. На каких участках: а) совершенная газом работа A; б) полученное газом тепло Q больше (меньше) нуля?
Задача 12. Изобразить на диаграмме Т, V совершаемый идеальным газом цикл, состоящий: а) из двух изотерм и двух изобар; б) двух изобар и двух изохор.
Задача 13. Изобразить на диаграмме Т, р совершаемый идеальным газом цикл, состоящий: а) из двух изотерм и двух изохор; б) двух изохор и двух изобар.
Задача 14. Изобразить на диаграмме Т, S совершаемый идеальным газом цикл, состоящий из двух изохор и двух изобар.
Задача 15*. Круговой процесс состоит из изотермы, адиабаты и двух изобар. Изобразить этот процесс на диаграмме Т, S (рис.22.17)

Задача
16*. Идеальный
газ (с известным )
совершает круговой процесс, состоящий
из двух изотерм и двух изохор. Изотермические
процессы протекают при температурах
![]() и
и![]()
![]() ,
изохорические – при объемахV1
и V2
(V2
в е
раз больше, чем V1).
Найти КПД цикла.
,
изохорические – при объемахV1
и V2
(V2
в е
раз больше, чем V1).
Найти КПД цикла.
