Занятие 26 дифракция света

Учебная цель: добиться понимания физической сущности явления дифракции. Научиться определять относительное распределение освещенности на экране в зависимости от размеров и формы неоднородностей, вызывающих дифракцию.

Литература

Основная: Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высшая школа, 1989. - Гл. 32, § 32.1 - 32.4.

Дополнительная: Савельев И.В. Курс общей физики. - М.: Наука, 1987. - Т. 2. - гл. 18, § 125 - 130.

Контрольные вопросы для подготовки к занятию

1. Дайте определение явления дифракции. При каких размерах препятствий можно наблюдать дифракционную картину?

2. Поясните принцип Гюйгенса и дополнение Френеля к принципу Гюйгенса.

3. Каков результат наложения вторичных когерентных волн? При каком условии получится усиление интенсивности света в данной точке? А при каком - ослабление света?

4. Как зависит интенсивность света от амплитуды интерферирующих волн?

5. Поясните метод зон Френеля:

- как строятся зоны Френеля?

- от чего зависит величина амплитуды волны, приходящей в данную точку экрана от одной из зон?

- зачем необходимо, чтобы радиусы соседних зон отличались на ? В каких фазах придут в одну точку волны от двух соседних зон?

- запишите суммарную амплитуду волны, если их т?

- сколько зон должно укладываться в препятствии, чтобы наблюдался максимум интенсивности света?

6. Дифракция на круглом отверстии:

- запишите и поясните выражение для амплитуды результирующего колебания в точке;

- при каком числе зон в данной точке будет наблюдаться максимум интерференции света? А при каком – минимум интерференции света?

- поясните дифракционную картину от круглого отверстия вблизи точки M (рис. 26.1).

7. В чем особенность построения зон Френеля при рассмотрении дифракции на диске?

8. Дифракция Фраунгофера на одной щели:

- когда наблюдается дифракция Фраунгофера?

- как строятся зоны Френеля?

- от чего зависит число зон Френеля?

- запишите и поясните условие дифракционного минимума (полная темнота) и условие дифракционного максимума.

9. Дифракция Фраунгофера на дифракционной решетке:

- напишите и поясните выражение разности хода лучей, идущих от двух соседних щелей;

- запишите и поясните условия: главного и дополнительных минимумов; главного максимума;

- как изменится распределение интенсивности в дифракционной картине при увеличении числа щелей?

Краткие теоретические сведения и основные формулы

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или, в более широком смысле, – любое отклонение волн от законов геометрической оптики.

Явление дифракции объясняется с помощью принципа Гюйгенса - Френеля, согласно которому каждая точка фронта волны может рассматриваться как источник вторичных сферических волн; вторичные волны когерентны и при наложении интерферируют.

Исходя из принципа Гюйгенса - Френеля, легко получить закон прямолинейного распространения света в свободной от препятствий однородной среде. Путь - точечный источник света (рис. 26.1),М - произвольная точка, в которой нужно найти амплитуду колебаний А. Построим сферическую волновую поверхность S, радиус R которой меньше расстояния на величинуL, причем R >>  и L >>  (  длина волны света). Искомая амплитуда А зависит от результата интерференции вторичных волн, излучаемых всеми участками ds поверхности S. Непосредственное решение этой задачи достаточно сложно, так как амплитуды и начальные фазы вторичных волн зависят от расположения соответствующих им источников ds по отношению к точке М. Поэтому Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение (метод зон Френеля).

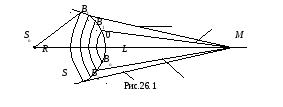
Френель разбил волновую поверхность S на кольцевые зоны (см. рис. 26.1) такого размера, чтобы расстояния от краев зоны до точки М отличались на т.е.Подобное разбиение фронта волны на зоны можно выполнить, проводя с центром в точкеМ сферы радиусом Так как колебания от соседних зон проходят до точкиМ расстояния, отличающиеся на то в точкуM они приходят в противофазах, и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

, (26.1)

где- амплитуды колебаний, возбуждаемых 1-й, 2-й, . . . ,т-й зонами Френеля.

Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол (рис. 26.2) между нормальюк поверхности зоны и направлением на точкуМ, т.е. действие зон постепенно убывает от центральной (около ) к периферическим. Кроме того, интенсивность излучения в направлении точкиМ уменьшается с ростом 0М и вследствие увеличения расстояния от зоны до точки М.

Учитывая оба эти фактора, можем записать

Общее число зон Френеля, умещающихся на полусфере, очень велико:

Если R = L = 0,1 м и  = 5 ^. 10^-7 м, то N  3 ^. 10⁵.

Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания А_т от некоторой т-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

. (26.2)

Тогда выражение (26.1) можно записать в виде

, (26.3)

так как по формуле (26.2) выражения, стоящие в скобках, равны нулю, а оставшаяся часть от амплитуды последней зоны ничтожна мала.

Таким образом, амплитуда, создаваемая в произвольной точке М сферической волновой поверхностью, равна половине амплитуды, создаваемой одной центральной зоной, радиус которой сравнительно мал (приR = L = 0,1 м и  = 5 ^. 10^-7 м,  1,6 ^. 10^-4 м). Следовательно, с достаточно большой точностью можно считать, что в свободном пространстве свет от источника в точкуМ распространяется прямолинейно.