II часть Примеры решения задач

Задача 1. Необходимо сжать воздух от объема 10^–2 м³ до объема 2 ^. 10^–3 м³. Как выгоднее сжимать: адиабатически или изотермически?

Дано:Решение

V

Для решения задачи необходимо сравнить работы адиабатического и изотермического сжатия.

Задачу можно решить: 1) качественно, построив графики адиабатического и изотермического сжатия; 2) аналитически, вычислив отношение работ

₁ = 10^–2 м³

V₂ = 2 ^. 10^–3 м³

1. Построим графики изотермического и адиабатического сжатия в координатах p, V.

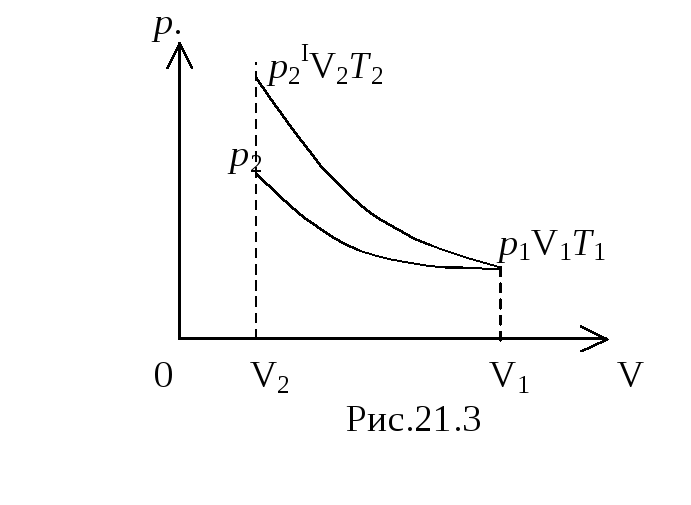
Начальное состояние воздуха определяется параметрами p₁ V₁T_1. Объем V₂ для обоих процессов является конечным и задан в условии задачи.

Уравнение адиабаты .

Уравнение изотермы .

Показатель адиабаты гдеi = 5, так как воздух состоит в основном из двухатомных газов;  = 1,4. Отсюда следует, что адиабата круче изотермы; при сжатии давление в адиабатическом процессе изменяется на большую величину, т. е. р₂^I > p₂ (см. рис. 21.3).

Работа в любом процессе может быть найдена как Интеграл графически изображается и может быть вычислен как площадь криволинейной трапеции, образованной кривой и ординатамиV₁ и V₂. Из графика видно, что площадь, ограниченная адиабатой больше, чем площадь под изотермой. Следовательно, работа адиабатического сжатия больше, чем изотермического. Поскольку работу при сжатии газа совершают внешние силы, то сжимать газ выгоднее изотермически.

2. Аналитическое решение задачи позволяет найти численное отношение работ А₁ и А₂ (А₁ – работа изотермического сжатия; А₂ – работа адиабатического сжатия):

Вычислим отношение:

.

Ответ: сжимать выгоднее изотермически.

Задача 2. Рассчитать, во сколько раз изменится число ударов, испытываемых 1 см² стенки сосуда за 1 с при двукратном увеличении объема двухатомного газа в следующих случаях: 1) изобарное расширение; 2) изотермическое расширение; 3) адиабатическое расширение.

Дано: Решение

1

Число ударов молекул в единичную площадку в единицу времени

. (1)

)р = const

2) Т = const

3) Q = 0

Каждая из N молекул, ударившихся о стенку, действует на стенку с силой

,

где m_i – масса молекулы, V_i – ее скорость, (m_i V_i) – изменение импульса молекулы при абсолютно упругом ударе. Молекула изменит при этом только направление скорости:

(m_i V_i) =  2 m_i V_i.

Сила удара молекулы о стенку будет равна

,

при ударе N молекул сумма сил

Давление газа на стенки сосуда

, , р = 2 m_i V_i Z.

Число ударов

. (2)

Будем считать массы молекул одинаковыми и скорость равной средней квадратичной.

Тогда

. (3)

Из основного уравнения молекулярно-кинетической теории

,

получим

подставив в уравнение (3), получим

.

Средняя квадратичная скорость

Окончательно получим

1. Изобарный процесс: р = const, следовательно, , так как .

Отношение т. е. при изобарном расширении число ударов убывает, но скорость молекулы увеличивается, так как температура возрастает, а значит и сила удара увеличивается, давление остается постоянным.

2. Изотермический процесс: Т = const,

При изотермическом расширении сила удара не изменяется, так как скорость остается постоянной, количество ударов уменьшается, следовательно, давление падает.

3. Адиабатический процесс: Q = 0.

- уравнение адиабаты;

(газ двухатомный);

Сравнивая результаты, видим, что в адиабатическом процессе число ударов уменьшается сильнее, чем в изотермическом, так как одновременно изменяются и объем, и температура, т. е. изменяется скорость движения молекулы и концентрация молекул. В результате давление падает сильнее, чем в изотермическом процессе.

Вывод: в изотермическом процессе расширения давление уменьшается только за счет уменьшения числа ударов, скорость молекул постоянна, а в адиабатическом процессе изменяется одновременно число ударов и сила удара. В этом состоит причина более резкого падения давления при адиабатическом расширении.

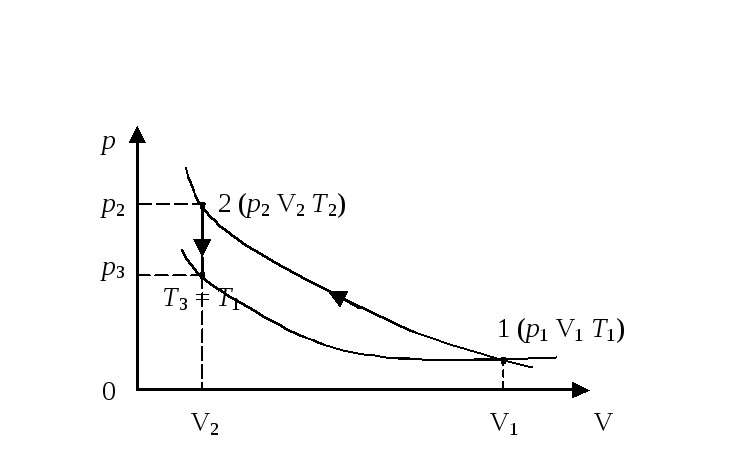
Задача 3. Двухатомный газ занимает объем V₁ = 0,5 л при давлении = 0,5^. 10⁵ Па. Газ сжимают адиабатически до некоторого давления и объемаV₂, затем при постоянном объеме V₂ охлаждают до первоначальной температуры. При этом давление становится равным = 10⁵ Па. 1) Начертите график этого процесса; 2) найдите объем V₂ и давление .

Дано:

= 0,5 ^. 10⁵ Па

= 10⁵ Па

V₁ = 0,5 л = 0,5 ^. 10^–3 м³

V₂ - ? - ?

Рис. 21.4