3.1. Погрешность вычисления значений функции.

Пусть непрерывно дифференцируемая функция,

- приближенные значения ее аргументов, для которых

- известные абсолютные погрешности.

Для погрешности приближенного значения функции по формуле Лагранжа получаем

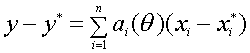, где

Заменяя , получаем

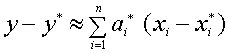
Оценка погрешности соответственно:

, где

Или  ( 5) ,

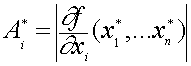 где  (6)

3.2. Погрешность суммы

Пусть задана функция

Тогда из (5) , (6) ,.

Для абсолютной погрешности получаем

.

Относительная погрешность

.

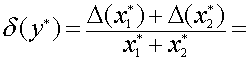
Пусть ,, тогда, т.е. при сложении приближенных величин относительная погрешность не возрастает.

3.3. Погрешность разности

Пусть задана функция

Тогда аналогично предыдущему абсолютная погрешность

.

Для относительной погрешности имеем формулу

.

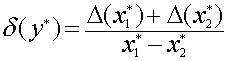Отсюда следует, что если приближенные значения иблизки друг к другу, то относительная погрешность их разностиможет оказаться намного большеи.

3.4. Погрешность произведения

Пусть задана функция 

Тогда абсолютная погрешность

.

Относительная погрешность

.

3.5. Погрешность частного

Пусть задана функция 

Тогда абсолютная погрешность

.

Относительная погрешность

3.6. Обратная задача оценки погрешности

Иногда возникает задача определения допустимой погрешности аргументов, при которой погрешность значений функции будет не более заданной величины .

Используем ранее полученное неравенство ( 6 )

.

Должно быть .

При n=1 вопрос решается однозначно:

При n>1 возможны разные подходы:

1. Считать погрешности всех аргументов одинаковыми

Тогда получаем 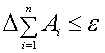, следовательно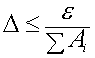

2. Считать, что вклад погрешности каждого аргумента в погрешность результата одинаков.  , тогда

Если для разных аргументов достижение определенной точности их задания существенно различается, то можно ввести функцию стоимости затрат на задание точкис заданными абсолютными погрешностямии искать ее минимум в области

, 

4. Вычисление погрешности арифметических действий в среде Mathcad .

Настройка среды MathCad (системные переменные ).

Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика  Опции.

1) Допустимая погрешность - значение системной переменной TOL (по умолчанию TOL =10^-3).

Установить TOL:=10^-5.

2) Изменение количества цифр в результате после разделяющей точки

производят во вкладке Результат диалогового окна Количество десятичных позиций команды Формат  Результат.

Установить равным 6 (по умолчанию равно 3) , что на 1 больше порядка величины TOL – для возможности округления конечного результата .

Пример 4.1.Вычисление погрешности операций сложения , вычитания , умножения и деления.

Пусть числа x и y заданы с абсолютными погрешностями x иy

x : = 2.5378    x : = 0.0001                  y : = 2.536y : = 0.001

Тогда относительные погрешности чисел

, _,    ,     

Найдем погрешности суммы и разности чисел

S1 : = x + y       S1 : = x + y             

S1 = 1.1 x 10^-3      

S2 : = x - y       S2 : = x + y             

S2 = 1.1 x 10^-3       

Относительная погрешность разности в раз больше относительной погрешности суммы!

Пример 4.2. Погрешность функции многих переменных.

Пусть x : = -3.59       y : = 0.467      z : = 563.2

По приведенным начальным условиям считаем, что абсолютные погрешности равны

x : = 0.01     y : = 0.001z : = 0.1

Значение функции равно : f ( x, y, z ) = 6.64198865

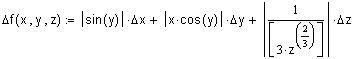
f ( x, y, z ) = 1.234 x 10 ^-3 f ( x, y, z ) = 8.196 x 10 ^-3    

 

Пример 4.3. Постановка задачи:

Дан ряд .

Найти сумму ряда S аналитически.

Вычислить значения частичных сумм ряда S=и найти величину погрешности при значениях значениях=,,,,.

Построить гистограмму зависимости верных цифр результата от .

Аналитическое решение задачи:

S= =

,

.

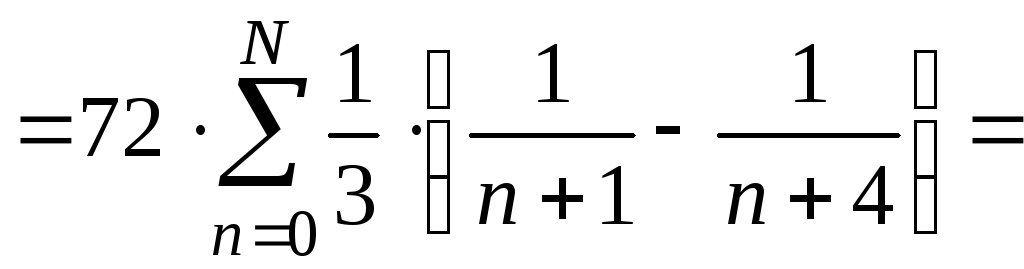
ОТВЕТ: S = = 44.

Введем функцию

S(N)= .

Тогда абсолютную погрешность можно определить с помощью функции

d(S(N)) =.

Tексты программ:

Гистограмма

Результаты вычислительного эксперимента:

Значение частичной Величина абсолютной Количество

суммы ряда погрешности верных цифр

S(10)=38.439560439 d(10)=5.56

S(100)=43.3009269 d(100)=0.699 2

S(1000)=43.9282153 d(1000)=0.072 3

S(10000)=43.992802 d(10000)=0.0072 4

S(100000)=43.9992802159957 d(100000)=0.00072 5

Вывод: Как видно из приведенного вычислительного эксперимента, увеличение числа членов ряда в 10 раз по сравнению с предыдущим случаем увеличивает число верных цифр в ответе на 1.