Раздел 2. Линейная алгебра

Матрица– прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов.

Матрица имеет вид 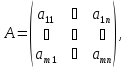или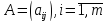- номер строки,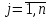- номер столбца.

Матрицу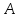называютматрицей размера 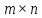и записывают 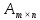. Числа-элементы матрицы.

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^т.

Например: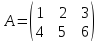, то.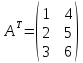

Действия над матрицами

1. Операция сложения матриц вводится только для матриц одинаковых размеров.

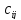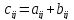Суммой двух матрицА_mxn=(а _ij)иВ_mxn=(в_ij)называется матрицаС_{mxn =}(), такая, что (i=1,2,…,m,j=1,2,…,n). ЗаписываютС=А+В

Например:Найти сумму матриц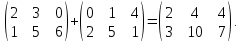

Аналогично определяется разность матриц.

2. Умножение матрицы на число

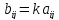Произведением матрицы А_mxn=(a_ij)на число kназывается матрицаB_mxn=(), такая что(i=1,2,…,m,j=1,2,…,n). Записывают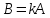

Например:Найти произведение матрицы А на число k, если 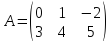, k=2.

3. Операция умножениядвух матриц водится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы 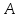_mxn=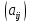на матрицу 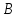_nxp=(b_jk) называется матрица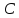_mxp=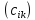такая, что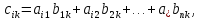где,.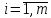

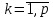Если матрицы квадратные одного размера, то произведения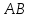и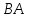всегда существуют.

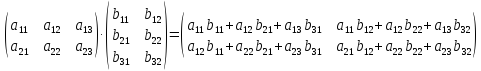
Например:Найти произведение матриц: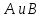

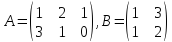
Произведение 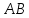не определено, т.к. число столбцов матрицы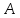(3) не совпадает с числом строк матрицы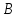(2). При этом произведение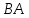определено:

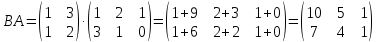
Пример 2: Выполнить действия над матрицами, где

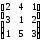A=,B=

Решение:

= ==

=;

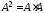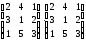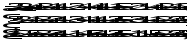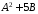=+5=+=

Ответ: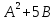

Любая квадратная матрица А имеет свой определитель. Прямоугольная, неквадратная матрица определителя не имеет.

Определителем (или детерминантом) второго порядка, соответствующим матрице

, называется число

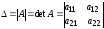, которое вычисляется по правилу

.

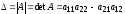Определителем (или детерминантом) третьего порядка, соответствующим матрице

, называется число

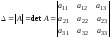
которое вычисляется по правилу «треугольника»

.

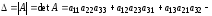
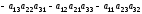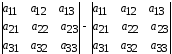
Минором М_ij элемента а_ij (i-номер строки, j-номер столбца) данного определителя называется определитель, полученный из данного путем вычеркивания i-строки и j-столбца.

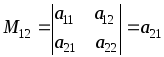–минор элемента а₁₂ определителя второго порядка;

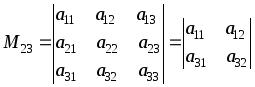–минор элемента а₂₃ определителя третьего порядка.

Алгебраическим дополнением элемента а_ij данного определителя называется число А_ij=(– 1)^i+j∙M_ij, где M_ij – минор элемента а_ij.

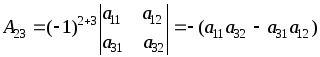–алгебраическое дополнение элемента а₂₃ определителя третьего порядка.

Система mлинейных уравнений сnнеизвестными имеет вид: 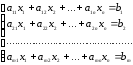, (1)

где 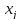- неизвестные,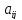- коэффициенты при неизвестных,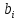- свободные члены,.

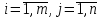Решением с.л.у. (1) называется такая совокупность чисел, при подстановке которых вместо неизвестных каждое уравнение обращается в верное равенство.

Система л.у. наз. совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.

Совместная с.л.у. наз. определённой, если она имеет единственное решение, и неопределённой, если имеет больше 1 решения.

Матричное уравнение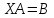решается умножением справа на матрицу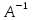обеих его частей.

Если определитель системы 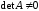, тогда матрица 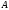имеет обратную. Следовательно, решение системы запишется в виде,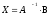

где

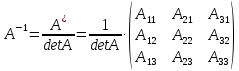
Пример 1: Решить систему линейных уравнений матричным методом

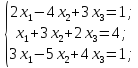
Решение:

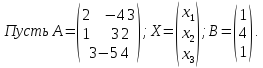
Тогда в матричном виде имеем:

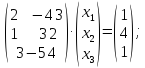
Вычислим det

det 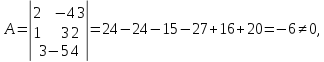значит матрица А-невырожденная, и существует обратная матрица

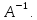
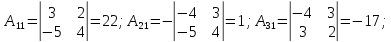
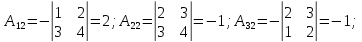
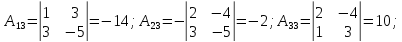
Тогда

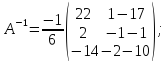
Значит .

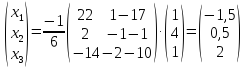Ответ: