1.2. Первый закон термодинамики.

Формулировки и аналитическое выражение первого закона термодинамики.

Первый закон термодинамики представляет собой одну из форм закона сохранения энергии, установленного в современном виде Гессом (1840 г), Майером (1842г), Джоулем (1842 г) и Гельмгольцем (1847 г).

Существует несколько формулировок закона сохранения энергии:

• Энергия не создается и не уничтожается;

• Вечный двигатель первого рода невозможен;

• В любой изолированной системе общее количество энергии постоянно.

В термодинамике применяется еще одна формулировка закона сохранения энергии, которая и является первым законом термодинамики. Этот закон оперирует с количествами теплоты и работы, которыми система обменивается с окружающей средой.

Предположим, что система совершает круговой процесс претерпевая изменения, например, сжатие, расширение, нагревание и т.д., при этом поглощает теплоту Q и совершает работу А. Рис. 1.7 а

Поскольку в самой системе в круговом процессе ничего не изменяется, согласно закону сохранения энергии

Q = А (1.5)

При этом будем считать, что + Q соответствует теплоте поглощаемой системой,

- Q теплоте, выделяемой системой.

Количество же работы в термодинамике принято считать положительным (+А), когда работа совершается системой и со знаком минус (-А), если совершается внешними силами над системой.

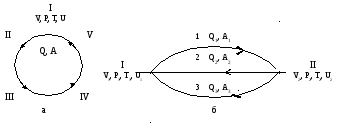
Рис.1.7 К формулировке первого закона термодинамики.

А теперь представим себе, что система совершает незамкнутый процесс по пути 1 (рис 1.6 б), переходя из состояния I в состояние II, при этом поглощает теплоту Q, и совершает работу А₁. Система перешла в иное состояние, в ней произошли какие-то изменения и, следовательно, количества теплоты и работы не будут равны.

Q₁≠ А₁(1.6)

Далее можно предположить, что система возвращается в положение I, но уже по пути 2, поглощая при этом теплоту Q₂и совершая работу А₂. и в этом случае следует считать, что Q₂≠ А₂.

В целом же система совершила круговой процесс и поэтому можно записать

Q₁+ Q₂= А₁+ А₂(1.7)

или

Q₂– А₂ = - (Q₁– А₁) (1.8)

Если представить, что наша система будет переходить из состояния I в состояние II по 1 пути, а а возвращаться по иному – 3,4,5..., то можно записать

Q₂ – А₂= Q₃– А₃ = Q₄– А₄ = …=Q_j – А_i = - (Q₁ – А₁) = const (1.9)

Отсюда следует, что разность Q– А для данного начального и конечного состояний не зависит от пути перехода и будет рвана изменению некоторого свойства системы. Этим свойством является внутренняя энергия. Поэтому, согласно предыдущему можно записать:

Q₁– А₁= U₂ – U₁(1.10)

или

Q– А =_ΔU = U₂ – U₁(1.11)

Данное соотношение можно представить в виде: Q=_ΔU + А (1.12) – которое является математической записью первого закона термодинамики.

Этот закон формулируется так:

Поглощенная системой теплота расходуется на увеличение внутренней энергии системы и на совершение ею внешней работы.

Уравнение (1.12) можно переписать в виде

- _ΔU = -Q+ А (1.13)

Т.е. убыль внутренней энергии системы расходуется на выделение теплоты и совершение работы.

Знак Δ (дельта, греч.) – означает конечную разность свойства системы. Для бесконечно малого изменения состояния уравнений 1.12 примет вид

δQ = dU + δA = dU + РdV + δA` (1.14)

где δА – сумма всех элементарных работ,

δA` - работа против гравитационных, электрических, магнитных и прочих сил, т.е. не связанная с изменением термодинамических параметров (так называемая полезная работа);

РdV – работа преодоления внешнего давления Р, необходимое для удержания системы в состоянии механического равновесия. Если на систему действует только постоянное внешнее давление, а другие силы отсутствуют, то A' = 0 и уравнение (1.14) принимает вид:

δQ = dU + РdV (1.15)

В этом уравнении Р можно считать давлением в системе только для равновесных (обратимых) процессов.

Процессы в которых участвуют системы могут протекать при различных условиях:

1. Изохорный процесс.

При изохорном процессе V= const, РdV = 0, согласно уравнению (1.15)

δQ_V = dU (1.16)

и для конечного изменения

Q_V = (1.17)

Таким образом, в изохорном процессе величина δQ_V приобретает свойства полного дифференциала и теплота не зависит от пути превращения. Если теплоту измерять в калориметре с постоянным объемом, то можно определять приращение (илиубыль) внутренней энергии системы. Реакции при V= const, могут быть осуществлены: а) в закрытой бомбе; б) между твердыми телами и жидкостями без выделения газа; в) между газами, если число молекул остается постоянным, например, H₂ + Cl₂ = 2HCl (газ)

2. Для изобарного процесса (р = const), в котором совершается только работа расширения уравнения (1.15), можно записать

δQ_р = dU + рdV = d (U + PV) = dН (1.18)

Сумма внутренней энергии и произведения объема вещества на внешнее давление называют энтальпией и обозначают буквой Н. Произведение рV численно равно работе, которую надо совершить, что бы данную систему ввести в пространство объемомV с давлением р. Следовательно, оно представляет собой ту потенциальную энергию системы, которая обусловлена давлением р в объемеV.Поэтому произведение рV– называютпотенциальной энергией давления.

Последняя, не имеет ничего общего с потенциальной энергией положения системы во внешнем силовом поле.

Термодинамическая система, в которой учитывается внутренняя энергия и потенциальная энергия давления, называется расширенной системой.

Интегрирование уравнения и простое преобразование дают:

Q_р = _ΔU + P_ΔV = U₂ – U₁ + р (V₂ – V₁) = (U₂ + рV₂) – (U₁ + рV₁) = Н₂ – Н₁ = _ΔН (1.19)

Следовательно, теплота, поглощенная в изобарном процессе, служит мерой приращения энтальпии системы. Так же, как и внутренняя энергия, энтальпия системы является функцией состояния.

3. Изотермический процесс

Передача теплоты при Т = const от одного тела к другому является квазистатическим процессом. Для идеального газа, а так же для реального при невысоких давлениях внутренняя энергия является функцией температуры. Поэтому при изотермических процессах U= const и уравнение (1.15) принимает вид:

δQ = рdV (1.20)

или

Q = А (1.21)

Следовательно, при изотермическом процессе сообщенная системе теплота целиком превращается в работу расширения.

4. Адиабатический процесс

При адиабатическом процессе δQ = 0 и уравнение (1.15) принимает вид:

δА = - dU (1.22)

или

А = - _ΔU (1.23)

Таким образом, при адиабатическом процессе работа расширения совершается системой за счет убыли ее внутренней энергии.